External corrosion of oil and gas pipelines: A review of failure mechanisms and predictive preventions
1
2022
... 石油和天然气在全球能源结构中占据着举足轻重的地位[1],它们不仅是现代工业的血液,更是推动全球经济发展的关键动力.在这些能源的输送过程中,管道输送以其高效性、安全性和成本效益成为了首选方式[2~5].油气在开采和输送过程中不可避免地含有腐蚀性杂质[6~8],这些腐蚀性的杂质会与管道内壁发生化学反应,引起管道的泄漏以及破裂,严重危害管道的完整性.管道腐蚀速率是评价管道腐蚀的关键因素,准确预测管道腐蚀速率关系到能源供应的稳定性,也直接影响到相关企业的经济效益和环境安全[9]. ...
Buckling resistance of an X80 steel pipeline at corrosion defect under bending moment
1
2021
... 石油和天然气在全球能源结构中占据着举足轻重的地位[1],它们不仅是现代工业的血液,更是推动全球经济发展的关键动力.在这些能源的输送过程中,管道输送以其高效性、安全性和成本效益成为了首选方式[2~5].油气在开采和输送过程中不可避免地含有腐蚀性杂质[6~8],这些腐蚀性的杂质会与管道内壁发生化学反应,引起管道的泄漏以及破裂,严重危害管道的完整性.管道腐蚀速率是评价管道腐蚀的关键因素,准确预测管道腐蚀速率关系到能源供应的稳定性,也直接影响到相关企业的经济效益和环境安全[9]. ...
Prediction of maximum pitting corrosion depth in oil and gas pipelines
0
2020
Development and outlook of China's pipeline transportation technologies under energy security strategy
0
2022
能源安全战略下中国管道输送技术发展与展望
0
2022
Efficient management and safe operation of gas pipelines under the background of "Dual Carbon"
1
2024
... 石油和天然气在全球能源结构中占据着举足轻重的地位[1],它们不仅是现代工业的血液,更是推动全球经济发展的关键动力.在这些能源的输送过程中,管道输送以其高效性、安全性和成本效益成为了首选方式[2~5].油气在开采和输送过程中不可避免地含有腐蚀性杂质[6~8],这些腐蚀性的杂质会与管道内壁发生化学反应,引起管道的泄漏以及破裂,严重危害管道的完整性.管道腐蚀速率是评价管道腐蚀的关键因素,准确预测管道腐蚀速率关系到能源供应的稳定性,也直接影响到相关企业的经济效益和环境安全[9]. ...
“双碳”背景下输气管道的高效管理与安全运行
1
2024
... 石油和天然气在全球能源结构中占据着举足轻重的地位[1],它们不仅是现代工业的血液,更是推动全球经济发展的关键动力.在这些能源的输送过程中,管道输送以其高效性、安全性和成本效益成为了首选方式[2~5].油气在开采和输送过程中不可避免地含有腐蚀性杂质[6~8],这些腐蚀性的杂质会与管道内壁发生化学反应,引起管道的泄漏以及破裂,严重危害管道的完整性.管道腐蚀速率是评价管道腐蚀的关键因素,准确预测管道腐蚀速率关系到能源供应的稳定性,也直接影响到相关企业的经济效益和环境安全[9]. ...
Analysis of oil and gas pipeline corrosion causes and influencing factors
1
2024
... 石油和天然气在全球能源结构中占据着举足轻重的地位[1],它们不仅是现代工业的血液,更是推动全球经济发展的关键动力.在这些能源的输送过程中,管道输送以其高效性、安全性和成本效益成为了首选方式[2~5].油气在开采和输送过程中不可避免地含有腐蚀性杂质[6~8],这些腐蚀性的杂质会与管道内壁发生化学反应,引起管道的泄漏以及破裂,严重危害管道的完整性.管道腐蚀速率是评价管道腐蚀的关键因素,准确预测管道腐蚀速率关系到能源供应的稳定性,也直接影响到相关企业的经济效益和环境安全[9]. ...
浅析油气管道腐蚀原因及影响因素
1
2024
... 石油和天然气在全球能源结构中占据着举足轻重的地位[1],它们不仅是现代工业的血液,更是推动全球经济发展的关键动力.在这些能源的输送过程中,管道输送以其高效性、安全性和成本效益成为了首选方式[2~5].油气在开采和输送过程中不可避免地含有腐蚀性杂质[6~8],这些腐蚀性的杂质会与管道内壁发生化学反应,引起管道的泄漏以及破裂,严重危害管道的完整性.管道腐蚀速率是评价管道腐蚀的关键因素,准确预测管道腐蚀速率关系到能源供应的稳定性,也直接影响到相关企业的经济效益和环境安全[9]. ...
Analysis of chemical corrosion mechanism of oil and gas pipelines and its protective measures
0
2024
油气管道化学腐蚀机理分析及其防护措施
0
2024
Study on bearing capacity of buried pipeline containing corrosion defects under external force
1
2018
... 石油和天然气在全球能源结构中占据着举足轻重的地位[1],它们不仅是现代工业的血液,更是推动全球经济发展的关键动力.在这些能源的输送过程中,管道输送以其高效性、安全性和成本效益成为了首选方式[2~5].油气在开采和输送过程中不可避免地含有腐蚀性杂质[6~8],这些腐蚀性的杂质会与管道内壁发生化学反应,引起管道的泄漏以及破裂,严重危害管道的完整性.管道腐蚀速率是评价管道腐蚀的关键因素,准确预测管道腐蚀速率关系到能源供应的稳定性,也直接影响到相关企业的经济效益和环境安全[9]. ...
含腐蚀缺陷埋地管道在外力作用下的承载力研究
1
2018
... 石油和天然气在全球能源结构中占据着举足轻重的地位[1],它们不仅是现代工业的血液,更是推动全球经济发展的关键动力.在这些能源的输送过程中,管道输送以其高效性、安全性和成本效益成为了首选方式[2~5].油气在开采和输送过程中不可避免地含有腐蚀性杂质[6~8],这些腐蚀性的杂质会与管道内壁发生化学反应,引起管道的泄漏以及破裂,严重危害管道的完整性.管道腐蚀速率是评价管道腐蚀的关键因素,准确预测管道腐蚀速率关系到能源供应的稳定性,也直接影响到相关企业的经济效益和环境安全[9]. ...
A review on pipeline integrity management utilizing in-line inspection data
1
2018
... 石油和天然气在全球能源结构中占据着举足轻重的地位[1],它们不仅是现代工业的血液,更是推动全球经济发展的关键动力.在这些能源的输送过程中,管道输送以其高效性、安全性和成本效益成为了首选方式[2~5].油气在开采和输送过程中不可避免地含有腐蚀性杂质[6~8],这些腐蚀性的杂质会与管道内壁发生化学反应,引起管道的泄漏以及破裂,严重危害管道的完整性.管道腐蚀速率是评价管道腐蚀的关键因素,准确预测管道腐蚀速率关系到能源供应的稳定性,也直接影响到相关企业的经济效益和环境安全[9]. ...
Carbonic acid corrosion of steel
2
1975
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
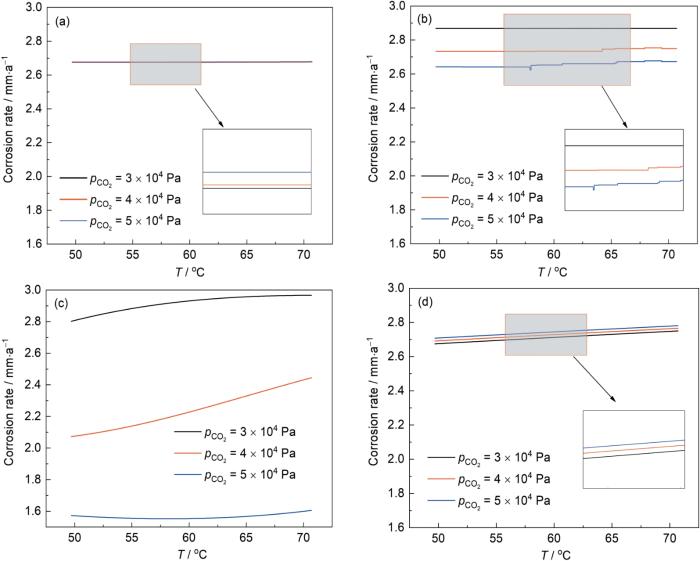
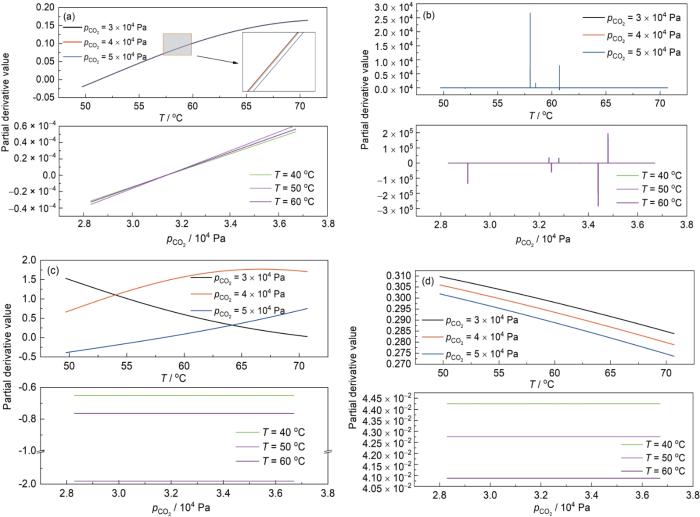
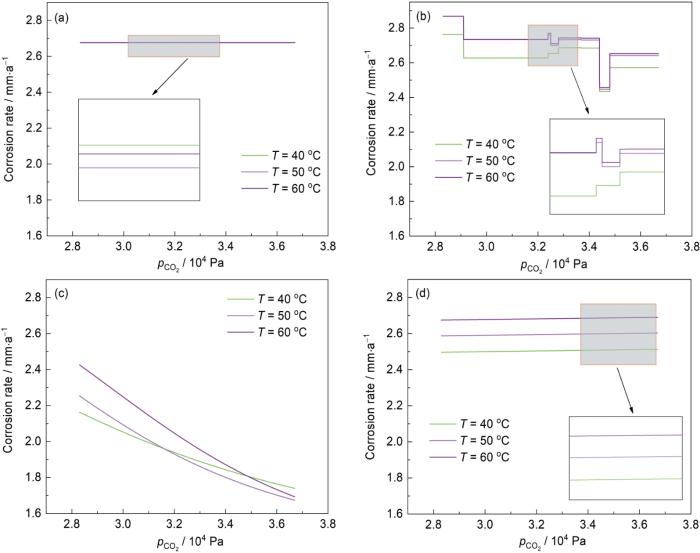
... 根据偏导数分析的结果可知,在所考察的模型有效域内,腐蚀速率关于温度的偏导数始终大于0.这一现象表明,在给定的公式适用条件下,腐蚀速率与温度之间存在单调递增的正相关关系.进一步地,根据De Waard等[10]提出的理论模型,在特定的CO2分压范围(3 × 104~6 × 104 Pa)内,当温度超过80 ℃时,由于腐蚀产物的形成,这些产物在管道金属表面形成一层保护膜,从而抑制腐蚀反应的进一步发展.相对地,在80 ℃以下,腐蚀速率随温度的升高而单调递增,未观察到由腐蚀产物引起的明显抑制效应.本研究所采用的实验对象和条件均位于前述模型所界定的适用范围之内,确保了研究结果的准确性和可靠性.因此,温度与管道的内腐蚀速率之间是单调递增关系,即: ...
Predictive model for CO2 corrosion engineering in wet natural gas pipelines
1
1991
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
Prediction of CO2 corrosion of carbon steel
0
1993
Influence of liquid flow velocity on CO2 corrosion: a semi-empirical model
1
1995
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
1
2001
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
A quasi 2-D localized corrosion model
1
2004
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
Integrated CO2 corrosion-multiphase flow model
1
2004
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
A revision of mechanistic modeling of mild steel corrosion in H2S environments
1
2021
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
Advances in corrosion growth modeling for oil and gas pipelines: a review
1
2023
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
Quantitative structure-activity relationship model for prediction study of corrosion inhibition efficiency using two-stage sparse multiple linear regression
1
2016
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
Predictive model for pitting corrosion in buried oil and gas pipelines
1
2009
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
Markov chain modelling for time evolution of internal pitting corrosion distribution of oil and gas pipelines
1
2016
... 管道内腐蚀预测的方法基本上可以概括为基于机理的方法、统计学方法以及基于机器学习(Machine learning,ML)的方法.基于机理的方法研究领域,De Waard和Milliams[10]利用管道内腐蚀的动力学过程和相关实验现场数据于1975年提出了DWM (DeWaard-Milliams)模型,主要考虑了温度和CO2分压,预测结果较为保守,后续又对模型进行了相关的改进[11~13],进一步考虑了其他的腐蚀影响因素.Interech公司提出了ECE (Electronic corrosion engineer)模型[14],该模型考虑了H2S的影响,但是预测结果忽略了pH的作用.Nesic模型[15,16]是著名的管道内腐蚀机理模型.该模型考虑了钢材表面的电化学模型、FeCO3产物膜特征和形成机理、腐蚀动力学生长模型等.尽管基于机理的模型在预测和分析方面充分考虑了潜在的腐蚀机理,但其复杂性较高,且需要大量实验数据确定模型参数[17,18],计算成本高,此外内管道腐蚀受多种腐蚀机制共同影响,影响因素之间存在相互作用和协同效应,传统的机理模型未能考虑.统计学方法主要是以传统线性回归为主,Al-Fakih等[19]提出的线性回归预测模型和Velázquez等[20]提出的多元回归模型是利用的统计方法进行的模型构建,但是这类模型通常只能捕捉简单的线性关系,面对复杂的非线性问题时,效果通常不佳.Ossai等[21]利用Markov链模型预测管道内腐蚀深坑的分布情况,较好的预测了时间序列,但是需要大量的实测数据来支持模型的参数估计和验证. ...
Main control factors and prediction model of flow-accelerated CO2/H2S synergistic corrosion for X65 steel
1
2022
... 机器学习方法在管道内腐蚀预测的应用越来越广泛[22].El-Abbasy等[23]基于回归分析和人工神经网络(Artificial neural network,ANN)的预测模型,在处理复杂的非线性问题上有着一定的优势.周逸轩等[24]将遗传算法(Genetic algorithm,GA)优化BP神经网络同时结合了核主成分(Kernel principal component analysis,KPCA)特征分析方法进行页岩气集输管道的腐蚀预测.刘军衡等[25]用麻雀搜索算法(Sparrow search algorithm,SSA)改进了支持向量机回归(Support vector regression,SVR)模型,优化后的模型预测效果明显提升.尽管数据驱动模型在捕捉变量之间的相关性方面表现出色[26],但是它们不能准确地理解输入和输出变量之间的因果关系[27].特别是在少样本或无样本区域,这些方法往往反应出参数关联特性与实际机理规律之间存在较大的偏差,且缺乏足够的物理可解释性.这使得这些模型常被称为“黑箱(Black box)[28]”. ...
Artificial neural network models for predicting condition of offshore oil and gas pipelines
1
2014
... 机器学习方法在管道内腐蚀预测的应用越来越广泛[22].El-Abbasy等[23]基于回归分析和人工神经网络(Artificial neural network,ANN)的预测模型,在处理复杂的非线性问题上有着一定的优势.周逸轩等[24]将遗传算法(Genetic algorithm,GA)优化BP神经网络同时结合了核主成分(Kernel principal component analysis,KPCA)特征分析方法进行页岩气集输管道的腐蚀预测.刘军衡等[25]用麻雀搜索算法(Sparrow search algorithm,SSA)改进了支持向量机回归(Support vector regression,SVR)模型,优化后的模型预测效果明显提升.尽管数据驱动模型在捕捉变量之间的相关性方面表现出色[26],但是它们不能准确地理解输入和输出变量之间的因果关系[27].特别是在少样本或无样本区域,这些方法往往反应出参数关联特性与实际机理规律之间存在较大的偏差,且缺乏足够的物理可解释性.这使得这些模型常被称为“黑箱(Black box)[28]”. ...
Internal corrosion rate prediction of shale gas gathering pipeline based on KPCA-GA-BP model
1
2024
... 机器学习方法在管道内腐蚀预测的应用越来越广泛[22].El-Abbasy等[23]基于回归分析和人工神经网络(Artificial neural network,ANN)的预测模型,在处理复杂的非线性问题上有着一定的优势.周逸轩等[24]将遗传算法(Genetic algorithm,GA)优化BP神经网络同时结合了核主成分(Kernel principal component analysis,KPCA)特征分析方法进行页岩气集输管道的腐蚀预测.刘军衡等[25]用麻雀搜索算法(Sparrow search algorithm,SSA)改进了支持向量机回归(Support vector regression,SVR)模型,优化后的模型预测效果明显提升.尽管数据驱动模型在捕捉变量之间的相关性方面表现出色[26],但是它们不能准确地理解输入和输出变量之间的因果关系[27].特别是在少样本或无样本区域,这些方法往往反应出参数关联特性与实际机理规律之间存在较大的偏差,且缺乏足够的物理可解释性.这使得这些模型常被称为“黑箱(Black box)[28]”. ...
基于KPCA-GA-BP模型的页岩气集输管道的内腐蚀速率预测
1
2024
... 机器学习方法在管道内腐蚀预测的应用越来越广泛[22].El-Abbasy等[23]基于回归分析和人工神经网络(Artificial neural network,ANN)的预测模型,在处理复杂的非线性问题上有着一定的优势.周逸轩等[24]将遗传算法(Genetic algorithm,GA)优化BP神经网络同时结合了核主成分(Kernel principal component analysis,KPCA)特征分析方法进行页岩气集输管道的腐蚀预测.刘军衡等[25]用麻雀搜索算法(Sparrow search algorithm,SSA)改进了支持向量机回归(Support vector regression,SVR)模型,优化后的模型预测效果明显提升.尽管数据驱动模型在捕捉变量之间的相关性方面表现出色[26],但是它们不能准确地理解输入和输出变量之间的因果关系[27].特别是在少样本或无样本区域,这些方法往往反应出参数关联特性与实际机理规律之间存在较大的偏差,且缺乏足够的物理可解释性.这使得这些模型常被称为“黑箱(Black box)[28]”. ...
Pipeline corrosion rate prediction based on SSA-SVR model
1
2025
... 机器学习方法在管道内腐蚀预测的应用越来越广泛[22].El-Abbasy等[23]基于回归分析和人工神经网络(Artificial neural network,ANN)的预测模型,在处理复杂的非线性问题上有着一定的优势.周逸轩等[24]将遗传算法(Genetic algorithm,GA)优化BP神经网络同时结合了核主成分(Kernel principal component analysis,KPCA)特征分析方法进行页岩气集输管道的腐蚀预测.刘军衡等[25]用麻雀搜索算法(Sparrow search algorithm,SSA)改进了支持向量机回归(Support vector regression,SVR)模型,优化后的模型预测效果明显提升.尽管数据驱动模型在捕捉变量之间的相关性方面表现出色[26],但是它们不能准确地理解输入和输出变量之间的因果关系[27].特别是在少样本或无样本区域,这些方法往往反应出参数关联特性与实际机理规律之间存在较大的偏差,且缺乏足够的物理可解释性.这使得这些模型常被称为“黑箱(Black box)[28]”. ...
基于ISSA-SVR模型的管道腐蚀速率预测
1
2025
... 机器学习方法在管道内腐蚀预测的应用越来越广泛[22].El-Abbasy等[23]基于回归分析和人工神经网络(Artificial neural network,ANN)的预测模型,在处理复杂的非线性问题上有着一定的优势.周逸轩等[24]将遗传算法(Genetic algorithm,GA)优化BP神经网络同时结合了核主成分(Kernel principal component analysis,KPCA)特征分析方法进行页岩气集输管道的腐蚀预测.刘军衡等[25]用麻雀搜索算法(Sparrow search algorithm,SSA)改进了支持向量机回归(Support vector regression,SVR)模型,优化后的模型预测效果明显提升.尽管数据驱动模型在捕捉变量之间的相关性方面表现出色[26],但是它们不能准确地理解输入和输出变量之间的因果关系[27].特别是在少样本或无样本区域,这些方法往往反应出参数关联特性与实际机理规律之间存在较大的偏差,且缺乏足够的物理可解释性.这使得这些模型常被称为“黑箱(Black box)[28]”. ...
Prediction on CO2 corrosion rate of tubing based on neural oblivious decision ensemble
1
2023
... 机器学习方法在管道内腐蚀预测的应用越来越广泛[22].El-Abbasy等[23]基于回归分析和人工神经网络(Artificial neural network,ANN)的预测模型,在处理复杂的非线性问题上有着一定的优势.周逸轩等[24]将遗传算法(Genetic algorithm,GA)优化BP神经网络同时结合了核主成分(Kernel principal component analysis,KPCA)特征分析方法进行页岩气集输管道的腐蚀预测.刘军衡等[25]用麻雀搜索算法(Sparrow search algorithm,SSA)改进了支持向量机回归(Support vector regression,SVR)模型,优化后的模型预测效果明显提升.尽管数据驱动模型在捕捉变量之间的相关性方面表现出色[26],但是它们不能准确地理解输入和输出变量之间的因果关系[27].特别是在少样本或无样本区域,这些方法往往反应出参数关联特性与实际机理规律之间存在较大的偏差,且缺乏足够的物理可解释性.这使得这些模型常被称为“黑箱(Black box)[28]”. ...
基于神经遗忘决策集成的油管CO2腐蚀速率预测
1
2023
... 机器学习方法在管道内腐蚀预测的应用越来越广泛[22].El-Abbasy等[23]基于回归分析和人工神经网络(Artificial neural network,ANN)的预测模型,在处理复杂的非线性问题上有着一定的优势.周逸轩等[24]将遗传算法(Genetic algorithm,GA)优化BP神经网络同时结合了核主成分(Kernel principal component analysis,KPCA)特征分析方法进行页岩气集输管道的腐蚀预测.刘军衡等[25]用麻雀搜索算法(Sparrow search algorithm,SSA)改进了支持向量机回归(Support vector regression,SVR)模型,优化后的模型预测效果明显提升.尽管数据驱动模型在捕捉变量之间的相关性方面表现出色[26],但是它们不能准确地理解输入和输出变量之间的因果关系[27].特别是在少样本或无样本区域,这些方法往往反应出参数关联特性与实际机理规律之间存在较大的偏差,且缺乏足够的物理可解释性.这使得这些模型常被称为“黑箱(Black box)[28]”. ...
Theory-guided data science: a new paradigm for scientific discovery from data
1
2017
... 机器学习方法在管道内腐蚀预测的应用越来越广泛[22].El-Abbasy等[23]基于回归分析和人工神经网络(Artificial neural network,ANN)的预测模型,在处理复杂的非线性问题上有着一定的优势.周逸轩等[24]将遗传算法(Genetic algorithm,GA)优化BP神经网络同时结合了核主成分(Kernel principal component analysis,KPCA)特征分析方法进行页岩气集输管道的腐蚀预测.刘军衡等[25]用麻雀搜索算法(Sparrow search algorithm,SSA)改进了支持向量机回归(Support vector regression,SVR)模型,优化后的模型预测效果明显提升.尽管数据驱动模型在捕捉变量之间的相关性方面表现出色[26],但是它们不能准确地理解输入和输出变量之间的因果关系[27].特别是在少样本或无样本区域,这些方法往往反应出参数关联特性与实际机理规律之间存在较大的偏差,且缺乏足够的物理可解释性.这使得这些模型常被称为“黑箱(Black box)[28]”. ...
Opening the black box: interpretable machine learning for geneticists
1
2020
... 机器学习方法在管道内腐蚀预测的应用越来越广泛[22].El-Abbasy等[23]基于回归分析和人工神经网络(Artificial neural network,ANN)的预测模型,在处理复杂的非线性问题上有着一定的优势.周逸轩等[24]将遗传算法(Genetic algorithm,GA)优化BP神经网络同时结合了核主成分(Kernel principal component analysis,KPCA)特征分析方法进行页岩气集输管道的腐蚀预测.刘军衡等[25]用麻雀搜索算法(Sparrow search algorithm,SSA)改进了支持向量机回归(Support vector regression,SVR)模型,优化后的模型预测效果明显提升.尽管数据驱动模型在捕捉变量之间的相关性方面表现出色[26],但是它们不能准确地理解输入和输出变量之间的因果关系[27].特别是在少样本或无样本区域,这些方法往往反应出参数关联特性与实际机理规律之间存在较大的偏差,且缺乏足够的物理可解释性.这使得这些模型常被称为“黑箱(Black box)[28]”. ...
Hidden fluid mechanics: learning velocity and pressure fields from flow visualizations
1
2020
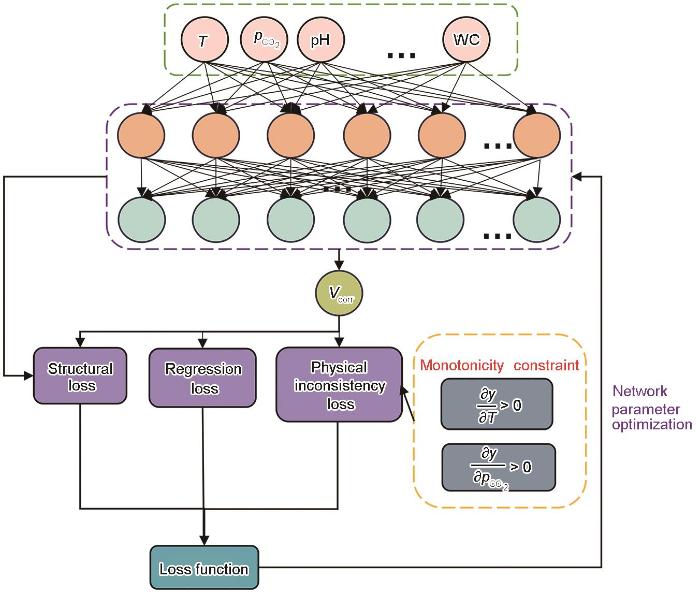
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
Temperature prediction of lithium-ion batteries based on physical information and deep neural network
1
2024
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
基于物理信息与深度神经网络的锂离子电池温度预测
1
2024
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
Physics-informed machine learning
1
2021
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
A physically consistent framework for fatigue life prediction using probabilistic physics-informed neural network
1
2023
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
Forecasting method for NO x emission in coal fired boiler based on physics-informed neural network
1
2024
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
基于物理信息神经网络的燃煤锅炉NO x 排放浓度预测方法
1
2024
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
Prediction method for biomass gasification product distribution based on physics-informed neural network
1
2024
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
基于物理信息神经网络的生物质气化产物分布预测方法
1
2024
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
Physics-guided prediction of corrosion rate inside gathering and transportation
1
2025
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
基于物理引导的集输管道内腐蚀速率预测及可解释性分析
1
2025
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
Research progress on internal corrosion of supercritical/dense-phase CO2 pipelines for CCUS
1
2024
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
CCUS超临界/密相CO2管道内腐蚀研究进展
1
2024
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
Effect of water content on corrosion behavior of X65 pipeline steel in supercritical CO2 fluids
1
2024
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
水含量对超临界CO2输送管道腐蚀的影响
1
2024
... 相关学者考虑到了机理模型和ML模型的局限性,考虑将特定领域的相关知识纳入到ML模型当中.由Raissi等[29]首次提出的物理信息神经网络(Physics-informed neural networks,PINN)是一种十分有应用前景的方法,在多个领域显示出了巨大的应用潜力.PINN将物理知识转化为约束条件,并将这些约束条件编码到神经网络的训练过程中[30],从而得出符合物理规律的可解释性的预测结果[31],减少了对大量数据的依赖,增强了模型的普适性.在最近的研究中,国内外相关学者在不同领域当中将物理知识神经网络相结合.Zhou等[32]将疲劳机制的物理学与概率物理信息网络相结合,提出了物理一致的疲劳寿命预测框架,利用灵敏度分析等验证了框架,具有较好的鲁棒性.任少君等[33]利用物理信息神经网络预测了燃煤锅炉的NO x 浓度,促使模型服从约束,提升模型在锅炉宽工况条件下的准确性.邓志平等[34]将实验数据和先验机理衔接,在人工神经网络当中嵌入边界约束和关键参数间的单调性关系,预测了生物质气化产物的分布.而在管道内腐蚀预测领域,PINN的应用相对较少.陈潜等[35]利用物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合,将不同腐蚀因素的普适性规律加入到机器学习当中,该研究对于物理机理的运用并没有与传统的机理经验模型相结合.管道内腐蚀涉及复杂的动力学和化学反应过程,管道内腐蚀以CO2腐蚀为主,受到多种腐蚀因素的影响[36,37],包括温度、管道内的CO2分压、pH等等.了解管道内腐蚀的相关机制并合理的捕捉它们之间的作用关系对于预测模型的开发至关重要. ...
Research for internal corrosion rate prediction of submarine oil and gas pipelines in service
1
2020
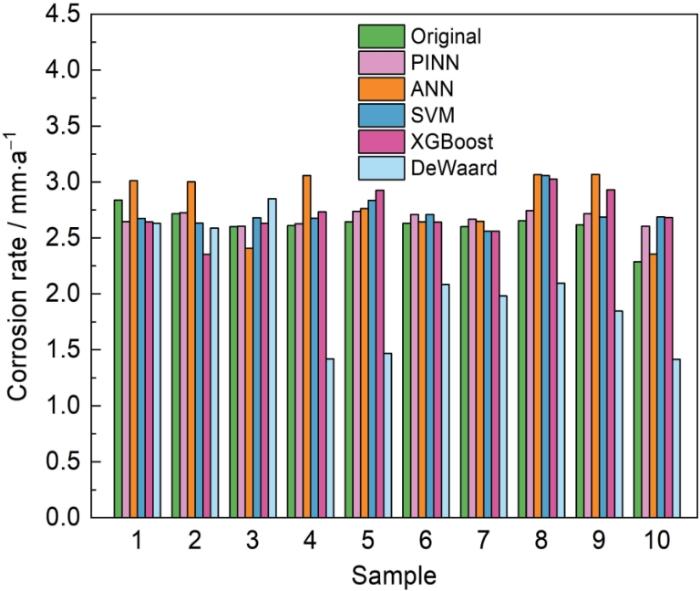
... 本文收集到的数据为我国海南省东部某油田群管段[38].其海底采用的是油气混输双层保温管道.材质为API SPEC 5L X52等级管线钢,管线直径为273.1 mm,壁厚12.7 mm,设计腐蚀余量为2 mm,设计温度为80 ℃.输送介质为油气水的混合物,主要腐蚀介质为CO2气体.收集到的相关数据共50组,相关数据及描述如表1所示. ...
在役海底油气管道内腐蚀速率预测研究
1
2020
... 本文收集到的数据为我国海南省东部某油田群管段[38].其海底采用的是油气混输双层保温管道.材质为API SPEC 5L X52等级管线钢,管线直径为273.1 mm,壁厚12.7 mm,设计腐蚀余量为2 mm,设计温度为80 ℃.输送介质为油气水的混合物,主要腐蚀介质为CO2气体.收集到的相关数据共50组,相关数据及描述如表1所示. ...