管道在服役过程中,受内压和土体位置移动的作用会产生拉伸应变[9,10],若管道上存在缺陷,则会在缺陷处产生塑性变形并形成应力集中[11]。当氢气在管道内输运时,氢分子会在金属管材表面吸附解离成为氢原子并进入钢中[12],进入钢中的氢原子在扩散过程中受应力作用会在高应力区富集,导致缺陷处的局部氢浓度升高,致使管材发生氢脆(HE)进而失效[13,14]。材料发生氢脆最典型的机理为氢促进局部塑性变形(HELP)和氢降低界面结合力(HEDE)。其中,HELP理论认为氢原子与位错结合降低位错运动能垒,从而提高位错的迁移率,引起局部塑性变形,产生孔洞并最终导致断裂[15]。随着钢中氢原子浓度的增加,HE的发生转变为HEDE机制,氢原子削弱晶格内Fe-Fe键,降低晶格间结合力,导致氢致断裂发生[16-18]。各种机制均指出氢脆发生受氢原子和应力的耦合作用影响[19]。氢在管道缺陷处富集的局部氢浓度越高,在较小服役应力下就会发生氢致开裂,并且最大氢浓度位置多为裂纹萌生的起点。因此,使用老旧管道输送掺氢天然气时,需要考虑氢与管道缺陷间的相互作用,评估缺陷对氢原子在管材内扩散富集行为的影响,明确管道缺陷处的氢浓度的位置分布,对临氢环境下含缺陷管道的安全评价具有重要意义。
国内外关于腐蚀管道安全评价的标准主要有API 579[20]、ASME B31G[21]、DNV RP F101[22]、BS 7910[23]和SY/T 6151-2009[24]等,但大多数标准的研究对象为单腐蚀缺陷,虽然DNV RP F101标准对多个腐蚀的相互作用有所涉及,但分析结果与实际相差较大。为此,Coulson和Worthingham[25]针对双腐蚀缺陷管道,研究了双腐蚀缺陷间的作用机理,提出了缺陷间的相互作用准则。O'Grady等[26]进一步研究得到不同缺陷间相互影响的轴向极限距离为25.4 mm。同时,孙溢彬等[27]基于有限元方法,考虑缺陷间的轴向间距和环向间距,对ASME B31G标准中的剩余强度计算公式进行了修正。此外,冯欣鑫等[28]根据轴向间距、环向间距的影响,简化了管道临界失效压力的计算方法。熊春宝等[29]还利用非线性有限元方法,研究矩形缺陷间距、深度和长度对X80管道失效压力的影响,并建立了失效压力计算公式。然而双腐蚀缺陷管道剩余强度敏感性因素众多,现有研究往往只分析了一部分要素,结论具有一定的局限性。虽然Andrews等[30]和Zhang等[31]的研究结果证明氢对腐蚀管道的失效行为和剩余强度有重要影响,但腐蚀管道的安全评价标准中并未考虑氢的作用,氢损伤对含腐蚀缺陷管道的影响机制也有待研究。因此,对含双腐蚀缺陷管道的氢扩散富集行为和氢浓度分布规律展开研究是十分必要的。
作者之前的工作[32]已对单腐蚀缺陷处氢原子的扩散和分布进行了研究,但双腐蚀缺陷间的应力耦合作用会对氢扩散富集产生更复杂的影响,形成与单腐蚀缺陷不同的规律/结论。为了探究双腐蚀缺陷下氢扩散富集行为,本文通过有限元模拟,耦合应力场和氢扩散场,探究氢原子在双腐蚀缺陷处的扩散富集行为以及氢浓度富集区的位置分布,并给出富集区氢浓度最大值以及所处位置,为临氢环境下含双腐蚀缺陷管道的安全评价提供理论支撑。
1 氢扩散模型
1.1 驱动力和扩散通量
式中,D为氢的扩散系数,4.32 × 10-11 m2·s-1[36];R为通用气体常数,8.4144 J·mol-1·K-1;T为绝对温度,取293.15 K;C为氢原子浓度,mol/m3;∇μ为化学势梯度。
式中,μ0为参考温度和压力下的化学势;σh为静水应力,等于主应力和的平均值;Vh为氢的偏摩尔体积,2 × 10-6 m3·mol-1[40]。
1.2 质量守恒方程
氢在金属晶格中的扩散是质量交换的过程,遵循质量守恒定律,质量守恒定律要求以表面S为界的任意体积V内总氢的变化率等于通过表面S的通量。考虑基体中扩散物质的非均匀溶解度差异、温度梯度以及压力梯度驱动,质量扩散过程可表示为[35]:
式中,∂/∂t为相对于时间的偏导数;n为V的单位外法向量。
将
应用散度定理得到简化形式的质量守恒方程为
这个方程是Fick第二定律的扩展形式,其中,C是扩散物质的摩尔浓度。
2 有限元模拟
在COMSOL有限元软件中,用于模拟一种稀物质运输的质量守恒方程为[41]:
式中,C为物质的浓度;D为物质的扩散系数;Ra为物质的反应速率,表示源项或汇项。对比
2.1 几何模型
为研究双腐蚀缺陷对氢原子在管道内的扩散和分布影响,建立了含两个内腐蚀缺陷的二维管道模型,如图1所示。所选管材为X52钢,屈服强度为359 MPa,抗拉强度为455 MPa,Young模量为207 GPa,Poisson比为0.3。模型长度为100 mm,壁厚为9.525 mm,两个腐蚀缺陷长度均为10 mm,深度为壁厚的20%。为了讨论氢在双缺陷处的分布随缺陷间距的变化,将两个缺陷间距设置为0、5、10、15和20 mm,并与尺寸相同的单个缺陷对比,在排除缺陷尺寸影响的条件下,分析双缺陷间的耦合作用与独立缺陷对氢富集行为不同的影响机制,即求解使耦合作用消失的极限距离。同理,将间距0 mm的双缺陷与长度20 mm的单缺陷对比,探究间距为0 mm的双缺陷组合与尺寸相同的单缺陷作用是否一致。图1中左侧箭头代表氢原子由管道内壁向管道外壁扩散,右侧箭头代表拉伸应变作用方向。
图1
图1
含双腐蚀缺陷管道的二维模型示意图
Fig.1
Schematic diagram of a two-dimensional pipe model with double internal corrosion defects
2.2 初始条件和边界条件
假设初始时没有氢原子进入管线钢内部,即钢中氢初始浓度为0,且在模拟过程中无氢通过模型边界。管道内壁与管道中的气体直接接触,将此接触面设为氢源边界,边界氢浓度设定为10 mol/m3 (1 mol/m3 ≈ 0.13 ppm[42])。管道上边界自由,下边界在径向上固定,左端设置固定约束,右端施加不同大小的轴向拉伸应变,分别为0%、0.1%、0.2%、0.5%、1%、2%和3%。腐蚀缺陷的存在导致管道上存在变化的局部应力应变。
2.3 管道弹塑性应力应变模型
对含双腐蚀缺陷的X52钢管段采用了弹塑性应力应变模型。选择各向同性硬化模型,其中,硬化函数σhard定义为[43]:
式中,σexp为从X52钢工程应力-应变曲线得到的实验应力函数;εeff为总有效应变;σy为X52钢的屈服强度,359 MPa;εp为塑性应变;σe为有效应力;E为Young模量;σe/E为弹性应变。管道弹塑性模型遵循von Mises屈服准则。
2.4 网格划分及模型求解
网格划分选用自由三角形网格,完整的网格包括2738个域单元和234个边界单元,不同模型单元数量略有不同。最大单元和最小单元分别为1 mm和0.004 mm,最大单元增长率为1.2,曲率因子为0.6,狭窄区域分辨率为1。使用MUMPS (multi-frontal massively parallel sparse)求解器计算,模拟氢原子扩散时间为5 × 106 s。
为了求解应力与氢扩散间的相互作用效应,使用COMSOL软件中固体力学、稀物质扩散和一般形式偏微分方程3个模块将固体力学场和氢扩散场耦合。其中,固体力学模块用于求解含缺陷管道在拉伸应变作用下的应力应变状态,稀物质扩散模块用于求解氢浓度分布状态,而一般形式偏微分方程用于表示
3 结果与讨论
3.1 应力和氢浓度分布
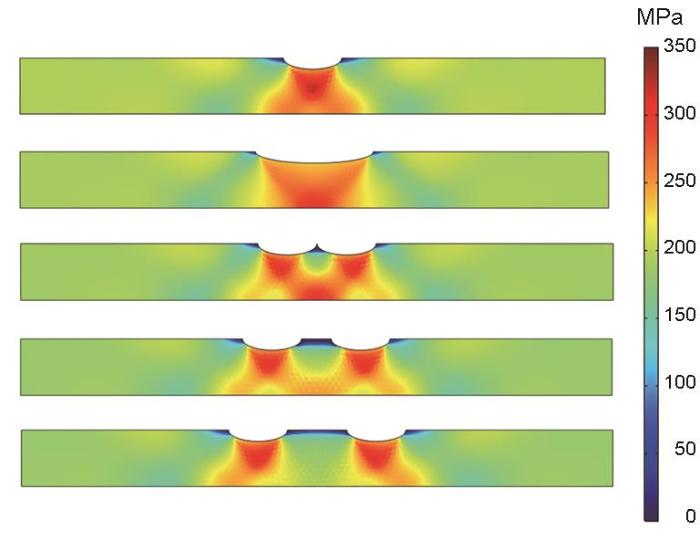
图2为0.5%拉伸应变下,长度10、20 mm单缺陷和相距0、5、10 mm双缺陷处的静水应力分布。拉伸应变导致在缺陷处产生静水应力集中,长度10 mm单缺陷的下方、管道中部位置静水应力最大,而长度20 mm单缺陷下方至管道外壁都有应力集中,但集中程度没有长度10 mm单缺陷明显。相距0 mm的两缺陷下方和两缺陷中间的管道外壁处均有静水应力集中区,3处应力大小一致;间距5 mm时,外壁处的集中程度减小,间距10 mm时此处应力集中消失,间距更大时与间距10 mm应力分布相同。
图2
图2
在0.5%的拉伸应变下,长度10、20 mm单缺陷和相距0、5、10 mm双缺陷处的静水应力分布
Fig. 2
Distributions of hydrostatic stress at single defect with length of 10 and 20 mm, double defects with spacing of 0, 5 and 10 mm under tensile strain of 0.5%
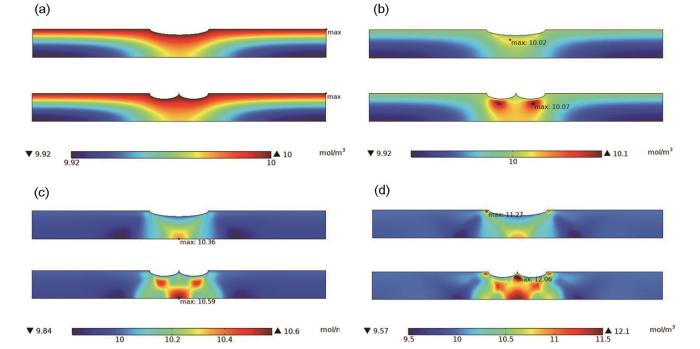
为展示最大氢浓度(Cmax)可能产生的位置,以图3中长度20 mm单缺陷、相距0 mm双缺陷在不同拉伸应变下最大值位置为例,扩散时间为5 × 106 s。可以看出,没有拉伸应变时,氢原子在单缺陷和双缺陷的管道中分布都较均匀,浓度最大值位于初始氢浓度边界处(管道内壁)。0.1%的拉伸应变下,Cmax位于一个缺陷的下方(未接触缺陷边界);0.2%的拉伸应变下,Cmax在模型底边(管道外壁);3%的拉伸应变下,Cmax移动到单个缺陷的上角或两缺陷中间的上部(未接触缺陷边界)。
图3
图3
在0%,0.1%,0.2%和3%的拉伸应变下,长度20 mm单缺陷与相距0 mm的双缺陷处的氢浓度分布
Fig.3
Distributions of hydrogen concentrations at single defect with a length of 20 mm and double defects with a spacing of 0 mm under tensile strains of 0% (a), 0.1% (b), 0.2% (c) and 3% (d)
3.2 缺陷间距及拉伸应变影响
表1 不同拉伸应变下,不同间距的双缺陷处氢浓度最大值
Table 1
| Tensile strain / % | Defect spacing/mm | ||||
|---|---|---|---|---|---|
| 0 | 5 | 10 | 15 | 20 | |
| 0 | 10 | 10 | 10 | 10 | 10 |
| 0.1 | 10.07 | 10.08 | 10.09 | 10.09 | 10.09 |
| 0.2 | 10.59# | 10.53 | 10.55 | 10.53 | 10.53 |
| 0.5 | 10.99# | 11.15* | 10.98 | 10.92 | 10.92 |
| 1 | 11.18* | 11.89* | 11.68* | 11.17 | 11.17 |
| 2 | 11.72* | 12.73* | 13.01* | 11.56 | 11.56 |
| 3 | 12.06* | 12.95* | 13.91* | 12.00 | 12.00 |
图4
图4
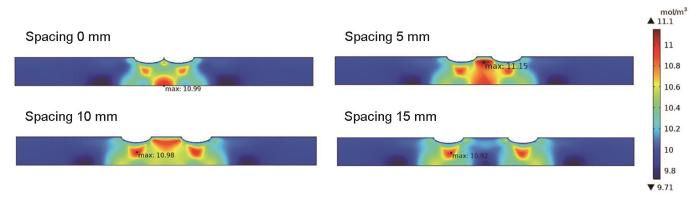
0.5%的拉伸应变下,不同间距双缺陷处氢浓度分布
Fig.4
Distributions of hydrogen concentrations at double defects with different spacing (0, 5, 10 and 15 mm) under 0.5% tensile strain
图5
图5
1%的拉伸应变下,不同间距双缺陷处氢浓度分布
Fig.5
Distributions of hydrogen concentrations at double defects with different spacing (0, 5, 10 and 15 mm) under 1% tensile strain
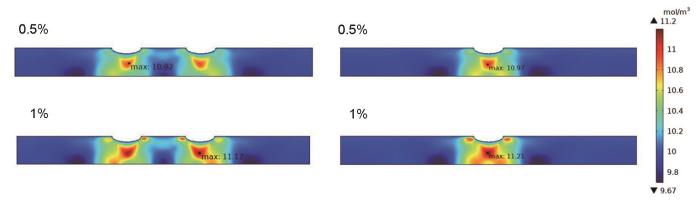
根据表1数据,当拉伸应变为0%时,不同间距双缺陷处最大氢浓度均为10 mol/m3,等于初始边界氢浓度,因为此时管道上没有明显的静水应力集中,氢原子在管道中均匀分布。施加拉伸应变后,最大氢浓度增大超过10 mol/m3,说明在拉伸应变作用下,缺陷处的应力集中改变了氢原子的分布状态,使它们发生了局部富集。在0.1%的较小拉伸应变下,缺陷间距越大,Cmax越大,但应力集中程度都较小,所以浓度值上相差很微小,同时Cmax都位于一个缺陷下方。在0.2%拉伸应变下,仅相距0 mm的双缺陷处Cmax位置变到管道外壁处,此时最大浓度差仍然较小。拉伸应变为0.5%时,间距5 mm双缺陷处Cmax值明显增大为11.15 mol/m3,大于其他间距下的浓度值10.92~10.99 mol/m3,且如图4所示,间距5 mm双缺陷处氢富集区颜色比其他间距下更深,Cmax也移动到两缺陷中间上方,这是此处静水应力梯度和氢浓度梯度共同作用的结果。在1%的拉伸应变作用下,0、5、10 mm的Cmax都位于两缺陷中间上方,由于静水应力集中程度增强,浓度值上升超过15和20 mm距离的浓度,而相距15和20 mm缺陷处的浓度最大值位置仍保持不变。图5中,相距0和15 mm的缺陷处氢富集区是较小面积的黄色,Cmax分别等于11.18和11.17 mol/m3,相距5和10 mm为更大的红色区域,Cmax达到11.89和11.68 mol/m3。拉伸应变继续增大使双缺陷相距10 mm时的Cmax变为最大,达到13.91 mol/m3。随着应变的增大,静水应力值增大且局部集中程度提高,相同间距下,双缺陷处Cmax变大,应变从0%增加到3%,所有Cmax从10 mol/m3上升至12 mol/m3以上,且位置发生变化。含腐蚀缺陷管道的Cmax位置识别非常重要,它可能是氢原子浓度超过一定阈值时引发氢致开裂的起始位置。
模拟结果进一步证明,静水应力和氢浓度是氢扩散分布的主要驱动力,如
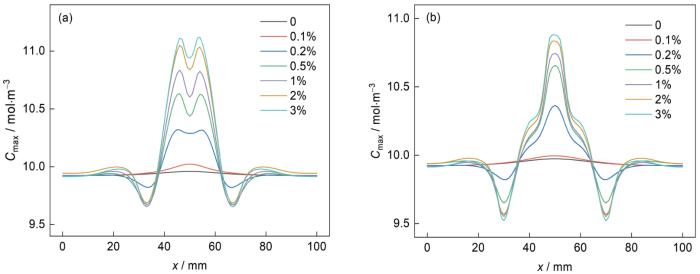
图6为不同间距的双腐蚀缺陷模型底边氢浓度分布,可以看出,图6a和b中缺陷间距较小,底边氢浓度只有一个最大值,两侧各有一个局部最大值,且高浓度区较集中,但5 mm间距的高浓度区宽于0 mm。随着缺陷间距增大到10 mm,如图6c所示,底边氢浓度出现两个最大值,高浓度区变得更宽。图6d中,当缺陷间距等于15 mm时,中间高浓度区分离,两侧的局部最大值变为整体的最大值,形成两个独立的高浓度区,证明双腐蚀缺陷间的相互作用对底边浓度影响减小。当腐蚀缺陷间距足够大时,其相互作用对氢浓度分布的影响可以忽略不计,而作为两个独立的缺陷考虑,更多结果将在3.4节讨论。不同拉伸应变下的底边氢浓度相差较大。0%和0.1%拉伸应变下底边氢浓度分布较均匀,中间氢浓度略高于两侧;施加0.2%的拉伸应变后,底边氢浓度变得不均匀,中间浓度值明显升高;0.5%以上的拉伸应变下,底边氢浓度分布曲线相同,但浓度值随应变增大。模型底边氢浓度分布结果表明,拉伸应变及双缺陷间距同时影响氢浓度分布,最终导致管道产生氢致裂纹位置变化。
图6
图6
不同间距的双腐蚀缺陷模型底边氢浓度分布
Fig.6
Linear distributions of hydrogen concentrations along the model bottom of double corrosion defects with a spacing of 0 mm (a), 5 mm (b), 10 mm (c) and 15 mm (d)
3.3 缺陷长度的影响
表2 不同缺陷长度下,不同间距的双缺陷处氢浓度最大值
Table 2
| Tensile strain/% | Defect length/mm | ||
|---|---|---|---|
| 8 | 10 | 12 | |
| 0 | 10 | 10 | 10 |
| 0.1 | 10.14 | 10.09 | 10.06 |
| 0.2 | 10.73 | 10.55 | 10.43 |
| 0.5 | 11.23 | 10.98 | 10.79* |
| 0.6 | 11.32 | 11.08* | 10.95* |
| 1 | 11.88* | 11.68* | 11.46* |
| 2 | 13.21* | 13.01* | 12.53* |
| 3 | 14.01* | 13.91* | 13.36* |
图7
图7
间距10 mm时,不同长度的双缺陷处氢浓度分布
Fig.7
Distributions of hydrogen concentrations at double corrosion defects with a spacing of 10 mm under different tensile strains and defect lengths
缺陷距离相同时,缺陷长度的增大使Cmax减小,图7中的氢富集区颜色逐渐变浅,0.5%和0.6%拉伸应变下Cmax分别从11.23和11.32 mol/m3降低到10.79和10.95 mol/m3,Cmax位置也从一个缺陷下方移动到两缺陷中间上方。但不同长度的缺陷处Cmax在不同大小的拉伸应变作用下发生位置移动。分析表2看出,0.5%的拉伸应变使长度12 mm的缺陷处Cmax移动到两缺陷中间上方,而0.6%的拉伸应变才能使长度10 mm的缺陷处Cmax位置改变,拉伸应变增大到1%时,长度8 mm的双缺陷Cmax才会移动。且缺陷长度越大,其氢浓度最大值在应变越小时上移。由此说明,缺陷尺寸会对氢浓度分布及最值位置产生影响,进而影响发生氢致开裂的位置。
3.4 双缺陷与单缺陷的对比
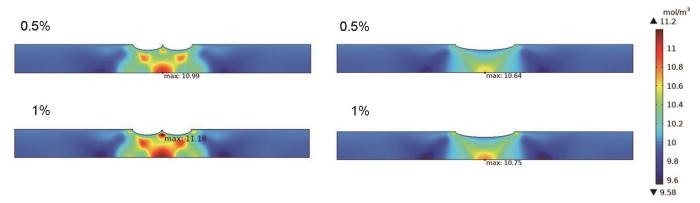
单缺陷与双缺陷处氢浓度最大值对比如表3所示。间距0 mm的双腐蚀缺陷与长度20 mm的单个缺陷、间距15 mm的双腐蚀缺陷与长度10 mm的单个缺陷在0.5%和1%的拉伸应变下的氢浓度分布如图8和9所示。由表3可知,相距0 mm的两个缺陷并不能等效为长度20 mm的单个缺陷,前者的最大浓度在不同的拉伸应变下始终大于后者,图8中两者的氢富集区形状和颜色深浅相差较大,且相距0 mm双缺陷的Cmax也在拉伸应变等于1%时从管道外壁上移至两缺陷中间,而1%拉伸应变下的单个20 mm缺陷的Cmax仍位于管道外壁,拉伸应变等于2%和3%时Cmax上移。双缺陷间的应力耦合作用随缺陷间距、缺陷尺寸和拉伸应变的变化复杂,因此双缺陷处氢浓度分布规律与单缺陷并不相同,Cmax的确定需要更详细地分析讨论。
表3 单缺陷与双缺陷处氢浓度最大值
Table 3
Tensile strain % | Defect spacing / mm | |||||
|---|---|---|---|---|---|---|
| 0 | 20 mm single defect | 10 | 15 | 20 | 10 mm single defect | |
| 0 | 10 | 10 | 10 | 10 | 10 | 10 |
| 0.1 | 10.07 | 10.02 | 10.09 | 10.09 | 10.09 | 10.10 |
| 0.2 | 10.59# | 10.36# | 10.55 | 10.53 | 10.53 | 10.58 |
| 0.5 | 10.99# | 10.64# | 10.98 | 10.92 | 10.92 | 10.97 |
| 1 | 11.18* | 10.75# | 11.68* | 11.17 | 11.17 | 11.21 |
| 2 | 11.72* | 11.13& | 13.01* | 11.56 | 11.56 | 11.55 |
| 3 | 12.06* | 11.27& | 13.91* | 12.00 | 12.00 | 11.94& |
图8
图8
间距0 mm双缺陷和单个长度20 mm缺陷在0.5%和1%的拉伸应变下氢浓度分布
Fig.8
Distributions of hydrogen concentrations at single defect with a length of 20 mm and double defects with a spacing of 0 mm under tensile strains of 0.5% and 0.1%
图9
图9
间距15 mm双缺陷和单个长度10 mm缺陷在0.5%和1%的拉伸应变下氢浓度分布
Fig.9
Distributions of hydrogen concentrations at double defects with a spacing of 15 mm and single defect with a length of 10 mm under tensile strains of 0.5% and 0.1%
拉伸应变相同时,相距15和20 mm时双缺陷处的Cmax值相等,与单个长度10 mm缺陷的氢浓度最大值相差不超过5%,且最大值位置都是在一个缺陷下方。图9中,间距15 mm双缺陷与单缺陷的氢富集区形状一致,颜色深浅相同,仅在双缺陷中间的非高浓度区略有差异,这种差异会随缺陷间距增大而消失。因此,两个长度10 mm缺陷相距大于15 mm时,对氢在缺陷处富集的影响作用与单个长度10 mm缺陷基本相同,不影响Cmax大小和位置,此时双缺陷处应力分布对氢浓度分布无耦合作用,可以看作独立缺陷进行分析。表3中单个长度10 mm缺陷处的Cmax会在拉伸应变较大(3%)时转移至上角,与长度20 mm的单个缺陷在2%和3%应变下的变化相同,可能是拉伸应变过大导致的氢浓度变化。
图10
图10
长度为10和20 mm单缺陷模型底边氢浓度分布
Fig.10
Linear distributions of hydrogen concentrations along the model bottom of single corrosion defect with a length of 10 mm (a) and 20 mm (b)
4 结论
本文建立了含双腐蚀缺陷管道模型,耦合应力场和氢扩散场,探究了双腐蚀缺陷处的氢富集情况,发现拉伸应变大小、缺陷间距、缺陷长度均会显著影响氢原子在缺陷处的扩散和富集行为,导致富集区最大氢浓度随拉伸应变、缺陷间距和长度不断变化,意味着不同条件下氢致裂纹起始位置将随之变化。主要结论如下:
(1) 无拉伸应变作用时,氢原子在管道上均匀分布,最大氢浓度是初始边界氢浓度;施加拉伸应变后,氢原子在腐蚀缺陷处发生局部富集,最大氢浓度超过边界浓度,并随拉伸应变的增大而升高。不同拉伸应变下,最大氢浓度会在一个缺陷下方、管道外壁和两缺陷中间上部3个位置变化,但不会接触到缺陷边界,始终保持一定的距离。
(2) 较小的拉伸应变(0.1%)下,不同间距的最大氢浓度相差很小;拉伸应变增大后(0.2%和0.5%),间距较小(0、5和10 mm)的最大氢浓度位置改变的同时数值升高明显,间距较大(15和20 mm)的最大氢浓度相对较小且位置不变。
(3) 双缺陷间距不变时,缺陷长度的增大使最大氢浓度减小,且最大氢浓度会在较小拉伸应变下从一个缺陷下方上移至两个缺陷的中间上部。
(4) 两个间距0 mm、长度均为10 mm的缺陷与一个长度20 mm的缺陷处氢浓度分布不同,而间距15 mm以上时可以看作两个独立的缺陷考虑其对氢分布的影响。
参考文献
Perspective of the role of hydrogen in the 21st century energy transition
[J].
Opinions of the State Council of the CPC Central Committee on completely, accurately and comprehensively implementing the new development concept and doing a good job of carbon peak and carbon neutralization
[EB/OL]. https://www.gov.cn/zhengce/2021-10/24/content_5644613.htm?eqid=e150e9910013963200000002647055a2,
中共中央国务院关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见
[EB/OL]. https://www.gov.cn/zhengce/2021-10/24/content_5644613.htm?eqid=e150e9910013963200000002647055a2,
Hydrogen energy: development prospects and materials
[J].
The cost of pipelining climate change mitigation: An overview of the economics of CH4, CO2 and H2 transportation
[J].
Computational fluid dynamic modeling of methane-hydrogen mixture transportation in pipelines: Estimating energy costs
[J].
Gas detection of hydrogen/natural gas blends in the gas industry
[J].
A comprehensive review on power-to-gas with hydrogen options for cleaner applications
[J].
Hydrogen and fuel cell technologies for heating: A review
[J].
Application of strain-based design for pipelines in permafrost areas
[A].
Strain-based reliability analysis of dented pipelines using a response surface method
[J].
Reliability and failure pressure prediction of various grades of pipeline steel in the presence of corrosion defects and pre-strain
[J].
Thermodynamics of spontaneous dissociation and dissociative adsorption of hydrogen molecules and hydrogen atom adsorption and absorption on steel under pipelining conditions
[J].
Hydrogen interaction with multiple traps: can it be used to mitigate embrittlement?
[J].
Hydrogen related degradation in pipeline steel: a review
[J].
Strain localization and hydrogen embrittlement
[J].
Mechanisms of hydrogen-enhanced localized plasticity: an atomistic study using α-Fe as a model system
[J].
Hydrogen-enhanced decohesion mechanism of the special Σ5(012)[100] grain boundary in Ni with Mo and C solutes
[J].
Hydrogen-assisted decohesion and localized plasticity in dual-phase steel
[J].
Hydrogen-induced degradation of high-strength steel pipeline welds: a critical review
[J].
Standard damage-assessment approach is overly conservative
[J].
Evaluating corroded pipe-conclusion: pressure calculation for corroded pipe developed
[J].
Calculation of residual strength of L245NCS steel pipe with double corrosion defects of different size
[J].
含不同尺寸双腐蚀缺陷L245NCS钢管剩余强度计算
[J].
Critical failure pressure of submarine pipeline with double corrosion defect
[J].
双腐蚀缺陷海底管道临界失效压力
[J].
Analysis on failure pressure of submarine pipelines under the influence of double corrosion defects
[J].
双腐蚀缺陷影响下的海底管道失效压力分析
[J].
Assessing damaged pipelines transporting hydrogen
[J].
Failure analysis of corroded high-strength pipeline subject to hydrogen damage based on FEM and GA-BP neural network
[J].
Finite element modeling of hydrogen atom diffusion and distribution at corrosion defect on aged pipelines transporting hydrogen
[J].
Deep trapping states for hydrogen in deformed iron
[J].
Quasichemical models of multicomponent nonlinear diffusion
[J].
Hydrogen transport near a blunting crack tip
[J].
Hydrogen permeability in a plasma nitrided API X52 steel
[J].
Numerical analysis of the coupling between hydrogen diffusion and mechanical behavior near the crack tip of titanium
[J].
The solution-diffusion model: a review
[J].
Numerical analysis of hydrogen transport near a blunting crack tip
[J].
Effects of hydrogen on the properties of iron and steel
[J].
Non-hydrostatic thermodynamics of chemical systems
[J].
Hydrogen embrittlement of steel pipelines during transients
[J].