非圆弯头冲蚀磨损数值模拟

doi:10.11902/1005.4537.2024.332

非圆弯头冲蚀磨损数值模拟

闫冲冲¹^,², 谢光明¹^,², 华剑^,¹^,², 曾云¹^,², 周思柱¹^,², 余泽坤¹^,²

1 长江大学机械工程学院荆州 434023

2 长江大学机械结构强度与振动研究所荆州 434023

Numerical Simulation of Erosion Wear on Non-circular Elbows

YAN Chongchong¹^,², XIE Guangming¹^,², HUA Jian^,¹^,², ZENG Yun¹^,², ZHOU Sizhu¹^,², YU Zekun¹^,²

1 School of Mechanical Engineering, Yangtze University, Jingzhou 434023, China

2 Mechanical Structures Strength and Vibration Research Institute, Yangtze University, Jingzhou 434023, China

通讯作者: 华剑，E-mail：huajian5410@yangtzeu.edu.cn，研究方向为机械结构强度与振动

收稿日期: 2024-10-10 修回日期: 2024-12-24

基金资助:

国家自然科学基金. 52174018
国家科技重大专项. 2016ZX05038-001-LH002

Corresponding authors: HUA Jian, E-mail:huajian5410@yangtzeu.edu.cn

Received: 2024-10-10 Revised: 2024-12-24

Fund supported:

National Natural Science Foundation of China. 52174018
National Science and Technology Major Project. 2016ZX05038-001-LH002

作者简介 About authors

闫冲冲，男，1998年生，硕士生

摘要

为减小普通弯头的冲蚀，提出一种非圆弯头。基于气固两相流理论，利用Fluent软件对非圆弯头流场进行分析，优化出抗冲蚀性较好的非圆弯头，并研究流速、质量浓度、颗粒直径3种因素对弯头冲蚀的影响。结果表明：长半轴(b)位于5.0~10.0、20.0~37.5时的非圆弯头具有抗冲蚀性，其中b = 30.0时抗冲蚀性最好，较普通弯头提高17.71%。非圆弯头和普通弯头的最大冲蚀速率随3种因素的增大递增，其中流速的影响最大。不论3种因素为何值，b等于30.0、22.5、35.0、32.5、27.5时的非圆弯头最大冲蚀速率始终小于普通弯头。普通弯头与b = 30.0时的非圆弯头的最大冲蚀速率差值随3种因素的增大递增。研究结果可为弯头的结构设计与改进提供新的思路。

关键词： 弯头 ; 气固两相流 ; 冲蚀磨损 ; 结构优化 ; 抗冲蚀

Abstract

Herein, a non-circular elbow is proposed, aiming to reduce the erosion of ordinary elbow. Based on the theory of gas-solid two-phase flow, the flow field of the non-circular elbow was analyzed using Fluent software, and the non-circular elbow with better erosion resistance was optimized and the effect of flow velocity, mass concentration and particle diameter on the erosion of the elbow was studied. The results show that: the non-circular elbows are resistant to erosion when their long half axis 1(b) is located in ranges of 5.0-10.0 and 20.0-37.5, while the best erosion resistance for that with b of 30.0 with an enhancement of 17.71% in contrast to the ordinary elbow. The maximum erosion rate of non-circular elbow and ordinary elbow increases with the increase of three factors, among which the flow rate has the greatest influence. Regardless of the value of the three factors, the maximum erosion rate of non-circular elbow with b equal to 30.0, 22.5, 35.0, 32.5 and 27.5 is always smaller than that of ordinary elbow. The difference between the maximum erosion rate of the ordinary elbow and the non-circular elbow with b equal to 30.0 increases with the increase of the three factors. The results of the study can provide new ideas for the structural design and improvement of the elbow.

Keywords： elbow ; gas-solid two-phase flow ; erosive wear ; structural optimization ; erosion resistance

PDF (1590KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

闫冲冲, 谢光明, 华剑, 曾云, 周思柱, 余泽坤. 非圆弯头冲蚀磨损数值模拟. 中国腐蚀与防护学报[J], 2025, 45(5): 1425-1432 DOI:10.11902/1005.4537.2024.332

YAN Chongchong, XIE Guangming, HUA Jian, ZENG Yun, ZHOU Sizhu, YU Zekun. Numerical Simulation of Erosion Wear on Non-circular Elbows. Journal of Chinese Society for Corrosion and Protection[J], 2025, 45(5): 1425-1432 DOI:10.11902/1005.4537.2024.332

天然气开采及输送中含有的微小固体颗粒会与管壁发生碰撞而造成壁面材料损失，这种现象称为冲蚀磨损^[1]。冲蚀磨损在弯头处较为严重，相关研究表明，弯头的冲蚀磨损程度约为直管的50倍^[2]，弯头在长期冲蚀磨损下会发生刺透，严重时还会引发爆炸^[3]。目前，减小普通弯头冲蚀磨损的方法有3种，一是调整流体介质参数：如杨湘愚等^[4]得出降低流速可以大大降低弯头的冲蚀磨损；董争亮等^[5]研究表明减小流速可以有效降低弯头的最大冲蚀磨损速率，这种方法虽然可以从根本上减小弯头的冲蚀磨损、延长使用寿命，但会影响流体介质输送量。二是改变弯头材料或加厚壁面：如Zou等^[6]制备的Al₂O₃增强高熵合金复合涂层相比于纯高熵合金涂层，其磨损率降低了一半；Bobzin等^[7]提出TiAlSiN涂层的冲蚀速率相对WC-Co硬质合金基体降低86%。这种方法虽然可以有效延长弯头使用寿命，但并未从根本上减小最大冲蚀速率，且成本较高。三是改变弯头结构：如黄钰棋等^[8]设计的非对称球形弯头抗冲蚀性能较普通弯头提高48.45%，且提高了颗粒运输效率；李睿等^[9]设计的半球形突起弯管具有较好的抗冲蚀作用，抗冲蚀性能比普通弯头提高36.36%。这种方法不仅可以从根本上减小弯头的冲蚀磨损、延长使用寿命且加工制造比较简单、成本较低。因此，结合实际情况来看，改变弯头结构是较好的方法，能从根本上改变颗粒轨迹流向、减小最大冲蚀速率，以延长使用寿命。

为此，本文在充分分析普通弯头的流体冲蚀特性后提出一种非圆弯头，利用Fluent软件对非圆弯头的流场进行分析，然后通过与普通弯头对比，优化出抗冲蚀性较好的非圆弯头，并探究流速、质量浓度、颗粒直径对两种弯头冲蚀磨损的影响。该研究结果可为弯头的结构设计和改进提供新的思路。

1 模型的提出和建立

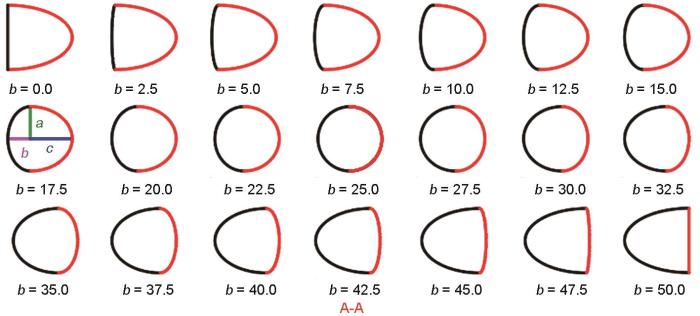
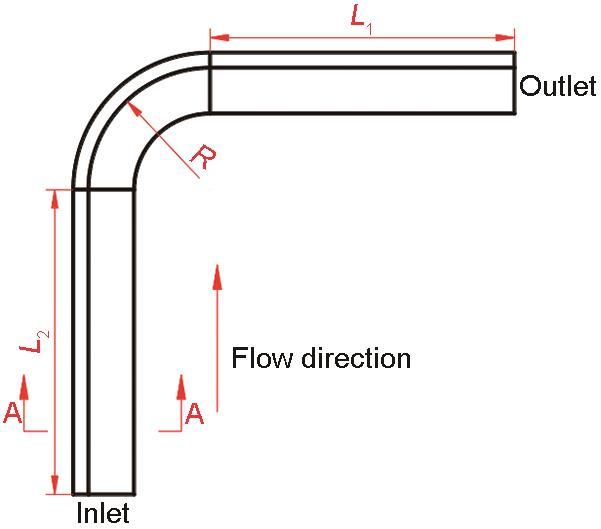
以管道内径50 mm、曲率半径100 mm的普通弯头为基本结构以方便非圆弯头的提出和建立。基于肖飞^[10]和莫丽等^[11]的相关研究依据，本文提出的非圆弯头与普通弯头有所不同，普通弯头的截面为圆形，该弯头的截面为非圆形，由两个半椭圆拼接而成，两个半椭圆重合的中心线为曲率线，为保证出口流量与普通弯头的出口流量相同，固定两个半椭圆组成的非圆截面面积与普通弯头的圆形截面面积始终相等。

非圆弯头的提出和模型的建立具体如下：普通弯头的半径为管道内径的一半，即25 mm，又因非圆弯头的非圆截面面积与普通弯头的圆形截面面积始终相等，由椭圆和圆的面积公式进行推导化简得到a·(b + c) = 1250，本文中a值与普通弯头的半径相等，即a = 25，从而得出b + c = 50，设定b、c的取值如表1所示，相对应的非圆截面形状如图1所示。上述模型建立中所提及的a、b、c分别代表短半轴1、2，长半轴1和长半轴2。图2为非圆弯头结构示意图，曲率半径(R)同上述普通弯头的R相等，即R = 100 mm，为使流体介质充分流经整个管线，将进出口段延长，即L₁ = L₂ = 250 mm。为方便后续弯头的描述，以b值代表不同结构的弯头；其中b = 25.0代表管道内径50 mm、R = 100 mm的普通弯头。图2中A-A代表剖视图符号，表示在A剖切线位置处的断面形状。

表1 非圆弯头截面中b、c的取值

Table 1 Values of b and c in non-circular elbows cross-section

a / mm	b / mm	c / mm
25	0.0	50.0
25	2.5	47.5
25	5.0	45.0
25	7.5	42.5
25	10.0	40.0
25	12.5	37.5
25	15.0	35.0
25	17.5	32.5
25	20.0	30.0
25	22.5	27.5
25	25.0	25.0
25	27.5	22.5
25	30.0	20.0
25	32.5	17.5
25	35.0	15.0
25	37.5	12.5
25	40.0	10.0
25	42.5	7.5
25	45.0	5.0
25	47.5	2.5
25	50.0	0.0

新窗口打开| 下载CSV

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 对应不同b值的弯头截面形状

Fig.1 Cross-sectional shapes of non-circular elbows corresponding to the different values of b

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 非圆弯头结构示意图

Fig.2 Schematic structure of non-circular elbow

2 数值模拟条件

2.1 边界条件

此次数值模拟中取连续相为甲烷(天然气的主要成分)，密度为0.6679 kg/m³，粘度为1.087 × 10^-5 Pa·s；离散相为固体颗粒，其密度为1800 kg/m³，颗粒直径为150 μm，质量浓度为0.05 kg/s。进口边界条件为速度进口，速度为18 m/s；出口边界条件为压力出口，出口压力为标准大气压；颗粒入射速度与进口流体速度相等，颗粒垂直进口截面均匀入射，进出口离散相边界类型为Escape，离散相模型DPM中Wall壁面采用Reflect类型。

2.2 数学模型

2.2.1 湍流模型

对管内天然气流动初步计算，其Reynolds数≥ 2300，可知管内流动为湍流流动，为减小计算误差，使用标准k-ε方程如下。

\frac{\partial (ρ k)}{\partial t} + \frac{\partial (ρ k u_{i})}{\partial x_{i}} \frac{\partial}{\partial x_{i}} [(μ + \frac{μ_{t}}{σ_{k}}) \frac{\partial k}{\partial x_{i}}] + G_{k} - ρ ε + S_{k}

(1)

\begin{array}{l} \frac{\partial (ρ ε)}{\partial t} + \frac{\partial (ρ ε u_{i})}{\partial x_{i}} \frac{\partial}{\partial x_{j}} [(μ + \frac{μ_{t}}{σ_{ε}}) \frac{\partial ε}{\partial x_{j}}] \\ + G_{1 ε} \frac{ε}{k} G_{k} - C_{2 ε} ρ \frac{ε^{2}}{k} + S_{ε} \end{array}

(2)

式中，ρ为流体密度，kg/m³；k为湍流动能，J；ε为湍流耗散率，W/m³；u_i为时均速度，m/s；μ为流体粘度，Pa·s；μ_t为湍动粘度系数；σ_k、σ_ε为k、ε方程的湍流Prandtl数，取1.0、1.3；G_k为平均速度梯度引起的湍动能k的产生项，x_i，x_j为空间坐标，m，i≠j；S_k、S_ε 为源项；G₁_ε =1.44，C₂_ε = 1.92为经验常数。

2.2.2 离散相控制方程

固体颗粒的运动轨迹由拉格朗日坐标系下的颗粒运动方程积分得到，由牛顿第二定律写出固体颗粒的运动控制方程如下^[12]。

\frac{d {\vec{u}}_{p}}{d t} = {\vec{F}}_{D} + {\vec{F}}_{P} + {\vec{F}}_{V M} + {\vec{F}}_{B}

(3)

{\vec{F}}_{D} = \frac{18 μ}{ρ_{p} d_{p}^{2}} \frac{C_{d} R e_{s}}{24}

(4)

{\vec{F}}_{P} = (\frac{ρ}{ρ_{p}}) \nabla p

(5)

{\vec{F}}_{V M} = \frac{1}{2} \frac{ρ d (\vec{u} - {\vec{u}}_{p})}{ρ_{d} d t}

(6)

{\vec{F}}_{B} = \frac{(ρ_{p} - ρ)}{ρ_{p}} \vec{g}

(7)

C_{d} = a_{1} + \frac{a_{2}}{R e_{s}} + \frac{a_{3}}{R e_{s}^{2}}

(8)

式中， ${\vec{F}}_{D}$ 、 ${\vec{F}}_{P}$ 、 ${\vec{F}}_{V M}$ 、 ${\vec{F}}_{B}$ 分别为单位质量固体颗粒受到的曳力、压力梯度力、附加质量力、重力和浮力的合力，N； $\vec{u}$ 为流体速度，m/s； ${\vec{u}}_{p}$ 为固体颗粒速度，m/s；d_p为颗粒直径，m；ρ为流体密度，kg/m³；ρ_p为颗粒密度，kg/m³； $\nabla$ P为压力梯度，Pa/m； $\vec{g}$ 为重力加速度，m/s²；Re_s为颗粒Reynolds数；C_d为曳力系数；a₁、a₂、a₃为常数。

2.2.3 颗粒壁面反弹模型

天然气中的固体颗粒会与壁面发生碰撞导致能量损失，使得颗粒反射速度低于入射速度，这种碰撞特性根据Grant和Tabakoff^[13]提出的随机颗粒-壁面反弹模型进行描述。

\begin{array}{l} e_{n} = 0.993 - 0.0307 α + 4.75 \times 10^{- 4} α^{2} \\ - 2.61 \times 10^{- 6} α^{3} \end{array}

(9)

\begin{array}{l} e_{t} = 0.998 - 0.029 α + 6.43 \times 10^{- 4} α^{2} \\ - 3.56 \times 10^{- 6} α^{3} \end{array}

(10)

式中，e_n为法向反弹系数；e_t为切向反弹系数；α为颗粒与壁面的碰撞角。

2.2.4 冲蚀速率模型

影响冲蚀速率的因素有很多，如颗粒直径、流体速度、颗粒碰撞角，局部流场的湍流等，本文使用的冲蚀速率模型方程如下^[14]。

E_{r} = \sum_{p = 1}^{N_{p a r t i c l e s}} \frac{m_{p} C (d_{p}) F (α) u_{p}^{b (u_{p})}}{A_{f a c e}}

(11)

式中，E_r为冲蚀速率，kg·m^-2·s^-1；N_particles为发生碰撞的颗粒数目；m_p 为颗粒质量浓度，kg/s；C(d_p )为颗粒直径函数；F(α)为碰撞角函数；b(u_p )速度指数函数；A_face为壁面单元表面积，m²。

2.3 网格剖分与独立性验证

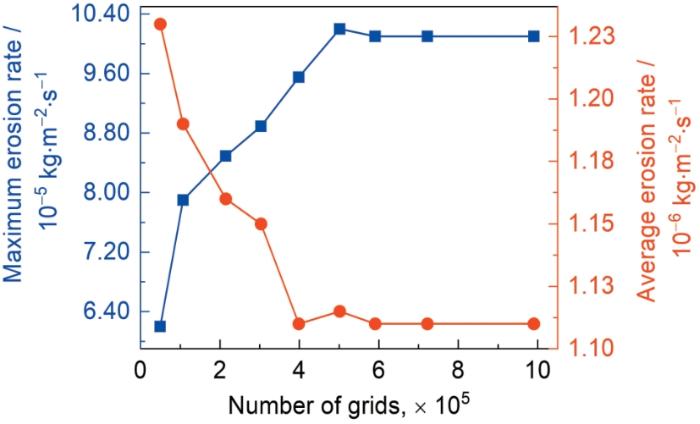
为提高网格质量和减少网格总数，网格剖分采用六面体网格；为得到近壁面处流体的真实流动状况，在流道圆周面添加边界层。然后将b = 12.5时的非圆弯头流道剖分为网格数量50022、107184、214865、303359、398361、501615、590976、722127、989989的9套网格逐一进行数值模拟，得到模拟结果如图3所示。由图3可知，当网格数量由50022增加至590976时，最大冲蚀速率逐渐增加、平均冲蚀速率逐渐减小且变化均较大，由590976增加至989989时，最大冲蚀速率和平均冲蚀速率均趋于稳定。因此，综合以上两个评价指标的分析结果，为减小误差最终选取网格数量722127进行后续数值模拟。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 网格独立性验证

Fig.3 Grid independence verification

2.4 模型验证

为验证本文使用的模型和模拟方法是否可行，采用文献[15]中的模拟值、文献[16]中的实验值分别以各文献中的弯管模型和边界条件利用本文使用的模型和方法进行数值模拟，得到结果图4和表2所示。从图4可以看出，本文模拟值、冲蚀形貌与文献模拟值、冲蚀形貌非常接近；从表2可以看出，实验值与本文模拟值误差在10%以内；从而验证了本文使用的模型和模拟方法是可行的。

图4

新窗口打开| 下载原图ZIP| 生成PPT

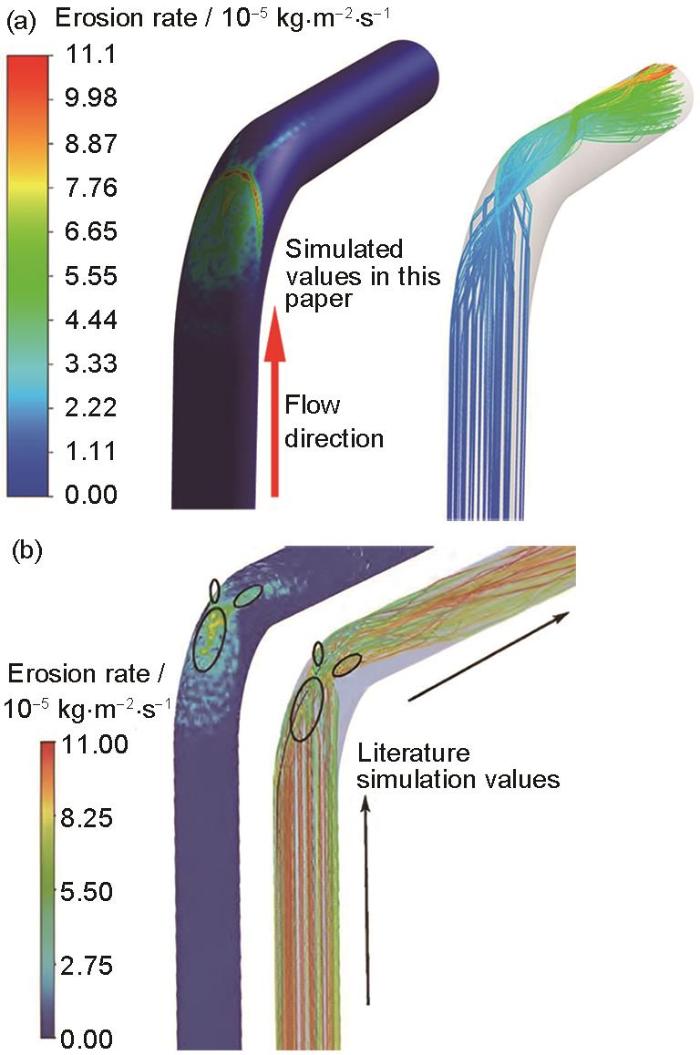
图4 数值模拟对比云图

Fig.4 Numerical simulation comparison cloud map: (a) simulated values in this paper, (b) literature simulation values

表2 实验与数值模拟对比值

Table 2 Comparison of experimental values and numerical simulation values

Maximum erosion rate / kg·m^-2·s^-1		Error / %
Experimental value	Simulation value	Error / %
2.92 × 10^-3	3.09 × 10^-3	5.82%
2.59 × 10^-3	2.75 × 10^-3	6.18%

新窗口打开| 下载CSV

3 结果与分析

3.1 流场分析

取b = 12.5时的非圆弯头进行数值模拟并提取压力、速度云图和流线图如图5所示。由图5a和b可以明显看出，进口段压力和速度变化比较均匀，这是因为进口段为直管、流体流动非常顺畅所致，图5c进口段流线的平稳性同样验证了该结果的准确性。弯头段压力和速度出现分层现象，且越靠近外侧管壁压力越大、速度越小，即压力和速度呈负相关，这是因为流体由进口段流入弯头段时，与管壁发生碰撞导致能量损失，使得流速降低、动能减小，即动能转化为压力能。出口段压力变化比较均匀，速度分层现象较为明显，尤其在出口端更为明显，这与图5c出口段上方流线密集、下方流线稀疏的结果一致。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 压力、速度云图和流线图

Fig.5 Pressure (a), velocity (b) cloud maps and flow diagram (c)

3.2 冲蚀结构优化

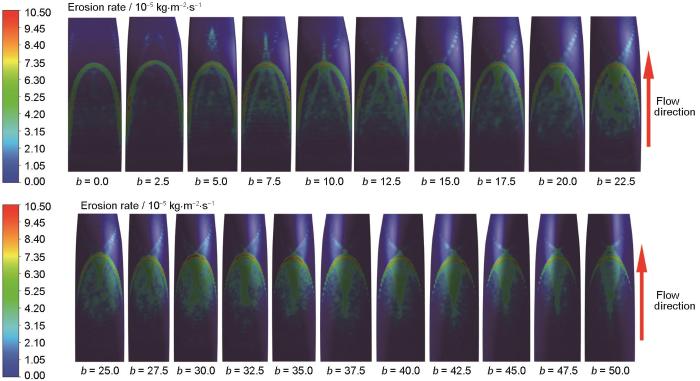
增大b值改变非圆弯头结构进行数值模拟，由模拟结果提取b值与最大冲蚀速率之间的关系曲线如图6所示，不同b值下的冲蚀分布云图和颗粒轨迹图如图7和8所示，图6中水平线代表普通弯头的最大冲蚀速率，为1.05 × 10^-4 kg·m^-2·s^-1。由图6可知，非圆弯头的最大冲蚀速率整体上先减小后增大。当b < 5.0时，非圆弯头的最大冲蚀速率大于普通弯头，即非圆弯头不具有抗冲蚀性能。当b位于5.0~10.0时，非圆弯头具有抗冲蚀性能。当b位于10.0~20.0时，除b = 12.5时非圆弯头具有抗冲蚀作用外，其余均无抗冲蚀作用。当b位于20.0~37.5时，非圆弯头整体上具有较好抗冲蚀效果，其中b = 30.0时的非圆弯头抗冲蚀效果最好，同普通弯头相比，抗冲蚀效果提高17.71%。当b > 37.5时，非圆弯头不但无抗冲蚀性能，反而在一定程度上加重了冲蚀。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 b值与最大冲蚀速率之间的关系

Fig.6 Maximum erosion rate as a function of b

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同b值下的冲蚀分布云图

Fig.7 Cloud maps of erosion distribution at different b values

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同b值下的颗粒轨迹图

Fig.8 Particle trajectories at different b values

由图7可以看出，不论b为何值，非圆弯头的冲蚀分布同普通弯头的冲蚀分布基本一致，均呈“椭圆形”形貌和二次产生的“V形”形貌。由图8可以看出，颗粒首次与管壁发生碰撞集中形成“椭圆形”形状，碰撞之后颗粒整体上呈V形扩散与管壁发生二次碰撞。b = 2.5、5.0、7.5、10.0时的非圆弯头，首次碰撞后颗粒并未呈V形扩散和二次碰撞趋势，这是因为弯头外侧壁近似平面结构，由于流场的主导作用、颗粒轨迹趋于直线；二是颗粒的惯性不足以使其在碰撞后发生明显偏转，即流体曳力在一定程度上抵消了颗粒的反弹趋势。

3.3 流速对弯头冲蚀磨损的影响

选取b = 30.0、22.5、35.0、32.5、27.5时的非圆弯头和b = 25.0时的普通弯头，分别以流速12、18、24、30、36 m/s进行数值模拟，得到流速与最大冲蚀速率之间的关系如图9所示。由图9可知，流速由12 m/s增加至36 m/s时，弯头的最大冲蚀速率最大增长24.10倍；随着流速的增大，弯头的最大冲蚀速率呈抛物线增长。从流体力学原理和冲蚀磨损理论分析来看：一是流速增大、固体颗粒动能急剧增加、对管壁的微切削作用及剪切力加强；二是流速增大、固体颗粒与管壁的冲击频率加快，导致管壁材料因疲劳扩展而产生剥落；三是流速增大、湍流强度增加，湍流中的涡流和速度波会加大对管壁的冲击；以上因素是导致冲蚀速率增大的主要原因^[17]。不论流速为何值，b = 30.0、22.5、35.0、32.5、27.5时的非圆弯头均具有抗冲蚀性能；随着流速的增大，b = 25.0时的普通弯头与b = 30.0、22.5、35.0、32.5、27.5时的非圆弯头的最大冲蚀速率差值逐渐增大。当流速< 27 m/s时，b = 30.0的非圆弯头抗冲蚀效果最好，当流速> 27 m/s时，b = 32.5的非圆弯头抗冲蚀效果最好。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同b值下最大冲蚀速率与流速之间的关系

Fig.9 Relationships between maximum erosion rate and flow velocity under different b values

3.4 质量浓度对弯头冲蚀磨损的影响

选取b = 30.0、22.5、35.0、32.5、27.5时的非圆弯头和b = 25.0时的普通弯头，以质量浓度分别为0.01、0.03、0.05、0.07、0.09 kg/s进行数值模拟，由模拟结果绘制质量浓度与最大冲蚀速率之间的关系如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同b值下最大冲蚀速率与质量浓度之间的关系

Fig.10 Relationships between maximum erosion rate and mass concentration under different b values

由图10得知，质量浓度从0.01 kg/s增加至0.09 kg/s时，弯头的最大冲蚀速率最大增长9.68倍；随着质量浓度的增加，弯头的最大冲蚀速率近似线性增长。分析其原因：质量浓度增加导致固体颗粒数目增加、致使固体颗粒在相同时间内、相同面积上与管壁的微切削频率、应力循环频率增加，从而使得管壁的冲蚀磨损较为严重^[18]。无论质量浓度如何变化，b等于30.0、22.5、35.0、32.5、27.5时的非圆弯头始终具有抗冲蚀作用，其中b = 30.0时的非圆弯头抗冲蚀效果最佳，b = 22.5、35.0、32.5、27.5时的非圆弯头抗冲蚀效果比较接近。随着质量浓度的增加，b = 30.0时的非圆弯头最大冲蚀速率与b = 25.0时的普通弯头最大冲蚀速率相差逐渐增大。

3.5 颗粒直径对弯头冲蚀磨损的影响

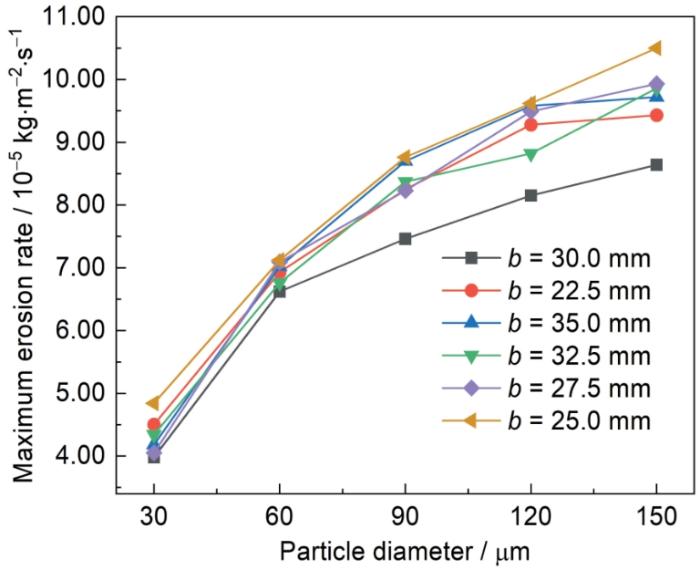
选取b = 30.0、22.5、35.0、32.5、27.5时的非圆弯头和b = 25.0时的普通弯头，取颗粒直径分别为30、60、90、120、150 μm进行数值模拟，由模拟结果得到颗粒直径与最大冲蚀速率之间的关系如图11所示。从图11可以看出，当颗粒直径从30 μm增大至150 μm时，弯头的最大冲蚀速率最大增长2.51倍；随着颗粒直径的增大，弯头的最大冲蚀速率逐渐增大。这是因为颗粒直径增大、质量增大(颗粒数目减少)、颗粒的冲击动能增加，颗粒与管壁造成的冲击较大(虽然颗粒数目减少、与管壁的碰撞次数减少，但较大的冲击动能弥补了因颗粒数目减少造成的能量损失)；同时颗粒直径增大、质量增大，颗粒的惯性力随之增大；最终导致冲蚀速率逐渐增大^[19]。无论颗粒直径为何值，b = 25.0时的普通弯头遭受的冲蚀磨损始终最为严重，b = 30.0时的非圆弯头遭受的冲蚀磨损始终最轻，其中，b = 25.0时的普通弯头最大冲蚀速率与b = 30.0时的非头弯头最大冲蚀速率的差值随颗粒直径的增大递增。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 不同b值下最大冲蚀速率与颗粒直径之间的关系

Fig.11 Relationships between maximum erosion rate and particle diameter under different b values

4 结论

(1) 对非圆弯头的流场分析得知，进口段压力和速度变化比较均匀；弯头段越靠近外侧管壁压力越大，速度越小；出口段压力变化比较均匀，速度出现分层现象。

(2) 冲蚀结构优化得出b位于5.0~10.0、20.0~37.5时的非圆弯头具有抗冲蚀性能，其中b = 30.0时抗冲蚀性能最好，同普通弯头相比抗冲蚀性能提高17.71%；非圆弯头的冲蚀形貌、颗粒轨迹与普通弯头的冲蚀形貌、颗粒轨迹基本一致。

(3) 非圆弯头的最大冲蚀速率变化趋势与普通弯头的最大冲蚀速率变化趋势相同，均随流速、质量浓度、颗粒直径的增大递增；分析各因素下最大冲蚀速率的数值及增长倍数，得出流速是最大冲蚀速率增长的主要因素。

(4) 不论流速、质量浓度、颗粒直径为何值，b等于30.0、22.5、35.0、32.5、27.5时的非圆弯头均具有抗冲蚀性能，其中b = 30.0时的非圆弯头抗冲蚀性能整体上最佳；b = 25.0时的普通弯头与b = 30.0时的非圆弯头的最大冲蚀速率差值随各因素的增大递增。

(5) 冲蚀结构优化出的具有抗冲蚀性能的非圆弯头同普通弯头相比，不仅可以减小冲蚀磨损、延长使用寿命，还可以保证流体介质输送量与普通弯头的流体介质输送量相同，对工程实际具有十分重要的参考价值和很好的应用前景。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

H Y

, Liu

, Wang

G Y

, et al.

Review on erosion-wear and protection of heat exchange surface in power station boilers

[J]. J. Chin. Soc. Corros. Prot., 2023, 43: 957