A review on diffusion modelling in hydrogen related failures of metals
3
2016
... 随着氢能的发展与广泛应用,将出现大量临氢结构如储氢容器、输氢管道.临氢结构的氢致开裂(Hydrogen induced cracking,HIC)或称氢脆(Hydrogen embrittlement,HE)问题亟待[1~12]解决,特别是含裂纹等缺陷的高压储、输氢容器、管道,其失效极可能导致重大燃烧、爆炸事故.事实上,早在1894年就有文献报道储氢压力容器的失效问题[1],但直到现在人们对氢致开裂机理的认识仍不透彻[2~4].不形成氢化物时,氢促进局部塑性变形(Hydrogen enhanced localized plasticity,HELP)和氢致键合力降低(Hydrogen enhanced decohesion,HEDE)是两个被广泛接受的HIC机理[4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
... [1],但直到现在人们对氢致开裂机理的认识仍不透彻[2~4].不形成氢化物时,氢促进局部塑性变形(Hydrogen enhanced localized plasticity,HELP)和氢致键合力降低(Hydrogen enhanced decohesion,HEDE)是两个被广泛接受的HIC机理[4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
... [1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
Dependence of hydrogen embrittlement on hydrogen in the surface layer in type 304 stainless steel
2
2014
... 随着氢能的发展与广泛应用,将出现大量临氢结构如储氢容器、输氢管道.临氢结构的氢致开裂(Hydrogen induced cracking,HIC)或称氢脆(Hydrogen embrittlement,HE)问题亟待[1~12]解决,特别是含裂纹等缺陷的高压储、输氢容器、管道,其失效极可能导致重大燃烧、爆炸事故.事实上,早在1894年就有文献报道储氢压力容器的失效问题[1],但直到现在人们对氢致开裂机理的认识仍不透彻[2~4].不形成氢化物时,氢促进局部塑性变形(Hydrogen enhanced localized plasticity,HELP)和氢致键合力降低(Hydrogen enhanced decohesion,HEDE)是两个被广泛接受的HIC机理[4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
... [2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
Hydrogen-induced cracking mechanism of precipitation strengthened austenitic stainless steel weldment
0
2015
A micromechanics approach to the study of hydrogen transport and embrittlement
7
2001
... 随着氢能的发展与广泛应用,将出现大量临氢结构如储氢容器、输氢管道.临氢结构的氢致开裂(Hydrogen induced cracking,HIC)或称氢脆(Hydrogen embrittlement,HE)问题亟待[1~12]解决,特别是含裂纹等缺陷的高压储、输氢容器、管道,其失效极可能导致重大燃烧、爆炸事故.事实上,早在1894年就有文献报道储氢压力容器的失效问题[1],但直到现在人们对氢致开裂机理的认识仍不透彻[2~4].不形成氢化物时,氢促进局部塑性变形(Hydrogen enhanced localized plasticity,HELP)和氢致键合力降低(Hydrogen enhanced decohesion,HEDE)是两个被广泛接受的HIC机理[4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
... [4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 本文考虑体心立方结构的屈服强度为250 MPa的低强度钢和屈服强度为1200 MPa的高强度钢两种材料,除屈服强度外其余参数均相同[18],为了保证对比性本文将低强度钢和高强度钢分别加载到89和132 MPa·m0.5 [4].选择这两种材料是因为两种材料在反应强度对氢脆的影响上具有代表性[4].主要材料参数如表2所示,其中有关氢陷阱的参数取决于对应的氢陷阱模型而未在表中给出. ...
... [4].主要材料参数如表2所示,其中有关氢陷阱的参数取决于对应的氢陷阱模型而未在表中给出. ...
... Main material properties
Table 2| Symbol | Value | Symbol | Value |
|---|
| E | 207 GPa[18] | NL | 8.46 × 1019 sites·mm-3 [18] |
| v | 0.3[18] | VH | 2.0 × 103 mm3·mol-1 [18] |
| n | 0.2[18] | DL | 1.27 × 10-2 mm2·s-1 [18] |
| β | 1[18] | ∆v/VA | 0.2826[4] |
| α | 6[18] | a | 2.8665 × 10-7 mm[13] |
<strong>3</strong> 结果与讨论<strong>3.1</strong> 扩散速度对氢浓度动态演化的影响鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... 以上分析表明对于低强度钢,即使初始NILS氢浓度很高其稳态浓度分布仍由氢陷阱控制,而对于高强度钢,在初始浓度高于4.24 × 10-9时可以采用无氢陷阱模型计算,如果进一步考虑到高强度钢裂尖或者缺口的塑性应变通常较低[4],则无氢陷阱的模型的使用范围将扩大.稳态氢浓度分布通常与氢致滞后断裂有关[29,30].Wang等[30]研究了AISI4130高强度钢缺口试样在初始氢浓度为6 × 10-8~3 × 10-7 (质量分数)的氢致滞后断裂,采用无氢陷阱模型计算氢扩散并对比实验结果,表明计算结果与实验吻合程度较好,对比本文计算的浓度范围可知其计算结果与本文符合.中低强度钢的裂尖和缺口根部附近不仅有较大的塑性变形同时也存在高的氢浓度,其裂纹易在此范围内萌生.如Olden等[28]研究了屈服强度为600 MPa的25%Cr双相不锈钢的氢致滞后断裂发现裂纹在缺口根部和近缺口处的铁素体相形核而并非静水应力最大处.对高强钢,裂尖或者缺口的塑性变形量较小,但其静水应力却很大,故裂纹易在静水应力附近形核,如Novak等[25]在研究AISI4130高强钢四点弯缺口试样在79 MPa氢气中热充氢后的氢致滞后断裂时表明裂纹在最大静水应力处附近萌生. ...
A thermo-mechanically-coupled theory accounting for hydrogen diffusion and large elastic-viscoplastic deformations of metals
1
2011
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
A generalised model of hydrogen diffusion in metals with multiple trap types
0
2015
Hydrogen embrittlement understood
2
2015
... 随着氢能的发展与广泛应用,将出现大量临氢结构如储氢容器、输氢管道.临氢结构的氢致开裂(Hydrogen induced cracking,HIC)或称氢脆(Hydrogen embrittlement,HE)问题亟待[1~12]解决,特别是含裂纹等缺陷的高压储、输氢容器、管道,其失效极可能导致重大燃烧、爆炸事故.事实上,早在1894年就有文献报道储氢压力容器的失效问题[1],但直到现在人们对氢致开裂机理的认识仍不透彻[2~4].不形成氢化物时,氢促进局部塑性变形(Hydrogen enhanced localized plasticity,HELP)和氢致键合力降低(Hydrogen enhanced decohesion,HEDE)是两个被广泛接受的HIC机理[4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
Modelling the coupling between hydrogen diffusion and the mechanical behaviour of metals
3
2016
... 随着氢能的发展与广泛应用,将出现大量临氢结构如储氢容器、输氢管道.临氢结构的氢致开裂(Hydrogen induced cracking,HIC)或称氢脆(Hydrogen embrittlement,HE)问题亟待[1~12]解决,特别是含裂纹等缺陷的高压储、输氢容器、管道,其失效极可能导致重大燃烧、爆炸事故.事实上,早在1894年就有文献报道储氢压力容器的失效问题[1],但直到现在人们对氢致开裂机理的认识仍不透彻[2~4].不形成氢化物时,氢促进局部塑性变形(Hydrogen enhanced localized plasticity,HELP)和氢致键合力降低(Hydrogen enhanced decohesion,HEDE)是两个被广泛接受的HIC机理[4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
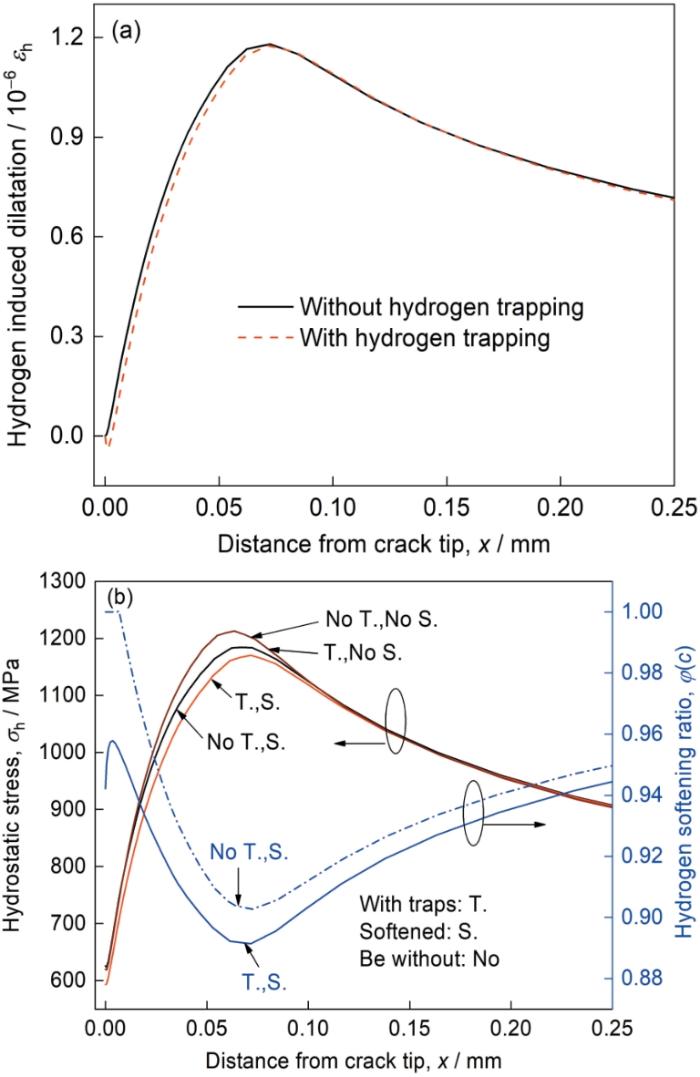
... 纯铁裂尖加载结束时裂尖附近氢致膨胀变形和静水应力如图9所示.可以看出氢致膨胀效应非常微弱,所导致的体积应变在10-6级别,主要是因为α铁的氢溶解度较低所致[8],有无氢陷阱对氢致晶格膨胀影响较小.图9b还表明氢致软化作用导致静水应力降低,在不考虑氢陷阱的情况下软化作用主要体现在静水应力峰值附近,而考虑氢陷阱时不仅静水应力峰值比没有考虑氢陷阱的低,而且在裂纹根部塑性区内其静水应力也比没有考虑氢陷阱的低.此外,考虑氢陷阱的软化系数较没有考虑氢陷阱的低,这是因为裂纹附近塑性变形区的氢陷阱能提供额外的氢浓度导致软化更加明显. ...
Numerical modeling of hydrogen diffusion in metals accounting for large deformations
1
2015
... 随着氢能的发展与广泛应用,将出现大量临氢结构如储氢容器、输氢管道.临氢结构的氢致开裂(Hydrogen induced cracking,HIC)或称氢脆(Hydrogen embrittlement,HE)问题亟待[1~12]解决,特别是含裂纹等缺陷的高压储、输氢容器、管道,其失效极可能导致重大燃烧、爆炸事故.事实上,早在1894年就有文献报道储氢压力容器的失效问题[1],但直到现在人们对氢致开裂机理的认识仍不透彻[2~4].不形成氢化物时,氢促进局部塑性变形(Hydrogen enhanced localized plasticity,HELP)和氢致键合力降低(Hydrogen enhanced decohesion,HEDE)是两个被广泛接受的HIC机理[4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
A coupled elastoplastic-transient hydrogen diffusion analysis to simulate the onset of necking in tension by using the finite element method
1
2010
... 随着氢能的发展与广泛应用,将出现大量临氢结构如储氢容器、输氢管道.临氢结构的氢致开裂(Hydrogen induced cracking,HIC)或称氢脆(Hydrogen embrittlement,HE)问题亟待[1~12]解决,特别是含裂纹等缺陷的高压储、输氢容器、管道,其失效极可能导致重大燃烧、爆炸事故.事实上,早在1894年就有文献报道储氢压力容器的失效问题[1],但直到现在人们对氢致开裂机理的认识仍不透彻[2~4].不形成氢化物时,氢促进局部塑性变形(Hydrogen enhanced localized plasticity,HELP)和氢致键合力降低(Hydrogen enhanced decohesion,HEDE)是两个被广泛接受的HIC机理[4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
Fractographic and numerical study of hydrogen-plasticity interactions near a crack tip
1
2006
... 随着氢能的发展与广泛应用,将出现大量临氢结构如储氢容器、输氢管道.临氢结构的氢致开裂(Hydrogen induced cracking,HIC)或称氢脆(Hydrogen embrittlement,HE)问题亟待[1~12]解决,特别是含裂纹等缺陷的高压储、输氢容器、管道,其失效极可能导致重大燃烧、爆炸事故.事实上,早在1894年就有文献报道储氢压力容器的失效问题[1],但直到现在人们对氢致开裂机理的认识仍不透彻[2~4].不形成氢化物时,氢促进局部塑性变形(Hydrogen enhanced localized plasticity,HELP)和氢致键合力降低(Hydrogen enhanced decohesion,HEDE)是两个被广泛接受的HIC机理[4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
Hydrogen-enhanced localized plasticity—A mechanism for hydrogen-related fracture
2
1994
... 随着氢能的发展与广泛应用,将出现大量临氢结构如储氢容器、输氢管道.临氢结构的氢致开裂(Hydrogen induced cracking,HIC)或称氢脆(Hydrogen embrittlement,HE)问题亟待[1~12]解决,特别是含裂纹等缺陷的高压储、输氢容器、管道,其失效极可能导致重大燃烧、爆炸事故.事实上,早在1894年就有文献报道储氢压力容器的失效问题[1],但直到现在人们对氢致开裂机理的认识仍不透彻[2~4].不形成氢化物时,氢促进局部塑性变形(Hydrogen enhanced localized plasticity,HELP)和氢致键合力降低(Hydrogen enhanced decohesion,HEDE)是两个被广泛接受的HIC机理[4~9].HELP理论认为氢原子通过屏蔽位错和障碍之间的弹性作用来增强位错的可移动性从而导致材料在微观上发生局部软化,进而可促使裂纹在低应力下萌生和扩展[10~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
... ~12].HEDE理论则认为集中于裂纹尖端的氢原子降低了金属原子间键合力使得断裂韧性下降[8].此外,各HIC机理均认为局部区域氢浓度达到临界值是其发生的前提[2,7],而显然临界氢浓度的达到是一个扩散主导的过程[1,11].因此,要评价含裂纹临氢结构是否会发生HIC,必须准确分析裂纹处的氢扩散及产生的氢浓度水平. ...
On the small scale character of the stress and hydrogen concentration fields at the tip of an axial crack in steel pipeline: effect of hydrogen-induced softening on void growth
5
2008
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... ,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
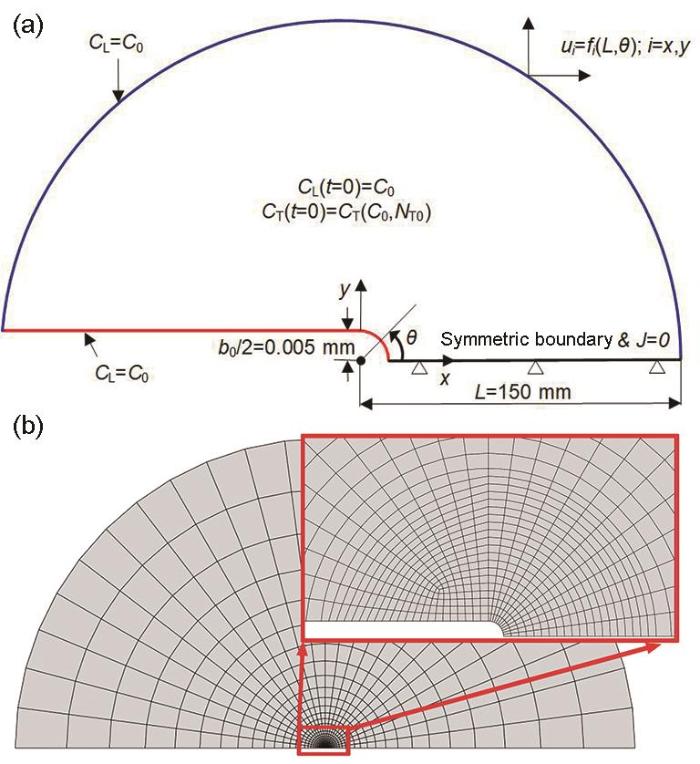
... 由于裂纹尖端附近小区域内同时存在静水应力梯度和较高局部塑性变形,故其最易表现出氢脆,因此本文研究平面应变I型裂纹在内氢脆情况下的氢扩散.Irwin小范围屈服下I型裂纹可以近似地用“边界层方法(Boundary layer approach)”研究[13](图2a).考虑到裂纹的对称性,边界层方法的几何模型为带有初始裂尖张开位移b0 = 0.01 mm、半径L =15000b0 = 150 mm的半圆形区域[18].边界条件和初始条件如图2a所示,初始时材料内NILS氢浓度由材料本身和氢环境(氢压)决定,可依据Sievert定律进行计算,如 式(16)所示: ...
... Main material properties
Table 2| Symbol | Value | Symbol | Value |
|---|
| E | 207 GPa[18] | NL | 8.46 × 1019 sites·mm-3 [18] |
| v | 0.3[18] | VH | 2.0 × 103 mm3·mol-1 [18] |
| n | 0.2[18] | DL | 1.27 × 10-2 mm2·s-1 [18] |
| β | 1[18] | ∆v/VA | 0.2826[4] |
| α | 6[18] | a | 2.8665 × 10-7 mm[13] |
<strong>3</strong> 结果与讨论<strong>3.1</strong> 扩散速度对氢浓度动态演化的影响鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... 由以上计算结果可知,氢陷阱的激活能对氢浓度分布具有决定性的影响,因此精确鉴别氢陷阱类型、测定结合能和陷阱密度十分重要[13].本文只考虑到单一陷阱模型,实际上金属内存在多种陷阱都有可能对氢脆产生重要影响,例如Li等[24]在研究AERMET 100钢中氢陷阱对氢脆机制的作用时发现被M2C碳化物捕获的氢会导致碳化物颗粒附近的基体发生解理开裂,而Novak等[25]则认为位错氢陷阱是AISI 4130钢氢脆的主要原因. ...
Behavior of hydrogen in steel during and after immersion in acid
1
1949
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
Hydrogen interaction with multiple traps: Can it be used to mitigate embrittlement?
2
2011
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 式中,β是平均每个溶剂原子对应的间隙位置数量;α是每个陷阱位置可容纳的氢原子数,用来描述氢陷阱的饱和性;θL和θT分别指氢占据的间隙位置和陷阱位置的比例(率).NL = NA/VM,NA = 6.023 × 1023 atoms·mol-1,为Avogadro常数,VM是溶剂金属的摩尔体积.氢陷阱密度与塑性变形量有关.Kumnick和Johnson[31]通过实验建立了纯铁中NT与等效塑性应变εp的关系,即 式(3).当无直接的NT实验数据时,通过假设位错线中每个原子平面含有一个陷阱位置,氢陷阱密度也可根据 式(4)由位错密度ρ估算[15,32],式中a为晶格常数. ...
A new analysis of the diffusion of hydrogen in iron and ferritic steels
1
1963
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
The diffusion and trapping of hydrogen in steel
4
1970
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 金属中的NILS和氢陷阱均可捕获氢原子,因此Oriani[17]将总氢浓度C定义为NILS中的氢浓度CL和陷阱中的氢浓度CT之和,即C = CL+ CT.浓度单位用H atoms·m-3来表示.考虑一个间隙位置可以容纳一个氢原子,单位体积中可容纳氢原子的间隙位置数目为NL,单位体积中的氢陷阱数目为NT,有: ...
... Oriani[17]认为处于陷阱中的氢和NILS中的氢处在实时的局部平衡,由于钢的氢溶解度极低即θL≪1,可推得θL和θT的显式关系为: ...
... 陷阱激活能和陷阱密度是表征氢陷阱的主要参数,然而对于位错氢陷阱的激活能,不同文献报道的值相差较大[24,25,32,41,42].Pressouyre[43]认为位错陷阱的平均激活能在28.6~35.5 kJ/mol之间.Oriani[17]利用电化学渗透法测出位错陷阱的激活能为27.6 kJ/mol.Kumnick和Johnson[31]通过冷轧形变的纯铁的电化学渗透则给出60 kJ/mol的值,他们推测对应的陷阱可能为位错核及割阶.Hirth[41]分析了以上数据后认为60 kJ/mol的激活能对应于混合位错核及刃型位错核,而20~30 kJ/mol的激活能则对应螺型位错核,0~20 kJ/mol对应位错的弹性应力场.Taketomi等[42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
Numerical analysis of hydrogen transport near a blunting crack tip
17
1989
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 氢扩散驱动力为化学式梯度,不仅浓度会影响化学势,静水应力也会对化学势产生作用[18].同时考虑浓度梯度和静水应力梯度对扩散的驱动,且认为扩散通量仅由NILS中氢的扩散贡献,忽略陷阱之间的扩散[33],扩散通量为: ...
... 氢原子对材料应力应变场的影响有两种方式:氢致晶格膨胀效应,可通过引入弹性体积应变项实现;氢致局部软/硬化,可通过在材料硬化方程中引入氢浓度作为内变量实现.在一般的有限变形情况下,流动法则可采用修正的Prandtl-Reuss方程描述[18],应变速率要扣除氢致晶格膨胀导致的应变速率: ...
... 由于裂纹尖端附近小区域内同时存在静水应力梯度和较高局部塑性变形,故其最易表现出氢脆,因此本文研究平面应变I型裂纹在内氢脆情况下的氢扩散.Irwin小范围屈服下I型裂纹可以近似地用“边界层方法(Boundary layer approach)”研究[13](图2a).考虑到裂纹的对称性,边界层方法的几何模型为带有初始裂尖张开位移b0 = 0.01 mm、半径L =15000b0 = 150 mm的半圆形区域[18].边界条件和初始条件如图2a所示,初始时材料内NILS氢浓度由材料本身和氢环境(氢压)决定,可依据Sievert定律进行计算,如 式(16)所示: ...
... 其中,s为溶解度系数;p (MPa)为环境氢活度,近似等于环境氢压(当环境氢压较小时).由于本文研究对象为钢,不考虑钢中微量合金元素对溶解度系数的影响,s取为定值6.53 × 1012 atoms H·mm-3·MPa-1/2 [18].力学边界条件为裂纹对称线取对称边界条件,半圆弧处的位移边界条件使用I型裂纹弹性位移场以恒定应力强度因子加载130 s后保载1.3×104 s(由试算知该时间可以达到99%的稳态浓度分布),加载位移场和应力强度因子如 式(17)[39]: ...
... 本文考虑体心立方结构的屈服强度为250 MPa的低强度钢和屈服强度为1200 MPa的高强度钢两种材料,除屈服强度外其余参数均相同[18],为了保证对比性本文将低强度钢和高强度钢分别加载到89和132 MPa·m0.5 [4].选择这两种材料是因为两种材料在反应强度对氢脆的影响上具有代表性[4].主要材料参数如表2所示,其中有关氢陷阱的参数取决于对应的氢陷阱模型而未在表中给出. ...
... Main material properties
Table 2| Symbol | Value | Symbol | Value |
|---|
| E | 207 GPa[18] | NL | 8.46 × 1019 sites·mm-3 [18] |
| v | 0.3[18] | VH | 2.0 × 103 mm3·mol-1 [18] |
| n | 0.2[18] | DL | 1.27 × 10-2 mm2·s-1 [18] |
| β | 1[18] | ∆v/VA | 0.2826[4] |
| α | 6[18] | a | 2.8665 × 10-7 mm[13] |
<strong>3</strong> 结果与讨论<strong>3.1</strong> 扩散速度对氢浓度动态演化的影响鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... -3 [
18]
| v | 0.3[18] | VH | 2.0 × 103 mm3·mol-1 [18] |
| n | 0.2[18] | DL | 1.27 × 10-2 mm2·s-1 [18] |
| β | 1[18] | ∆v/VA | 0.2826[4] |
| α | 6[18] | a | 2.8665 × 10-7 mm[13] |
<strong>3</strong> 结果与讨论<strong>3.1</strong> 扩散速度对氢浓度动态演化的影响鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... [
18]
VH | 2.0 × 103 mm3·mol-1 [18] | | n | 0.2[18] | DL | 1.27 × 10-2 mm2·s-1 [18] |
| β | 1[18] | ∆v/VA | 0.2826[4] |
| α | 6[18] | a | 2.8665 × 10-7 mm[13] |
<strong>3</strong> 结果与讨论<strong>3.1</strong> 扩散速度对氢浓度动态演化的影响鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... -1 [
18]
| n | 0.2[18] | DL | 1.27 × 10-2 mm2·s-1 [18] |
| β | 1[18] | ∆v/VA | 0.2826[4] |
| α | 6[18] | a | 2.8665 × 10-7 mm[13] |
<strong>3</strong> 结果与讨论<strong>3.1</strong> 扩散速度对氢浓度动态演化的影响鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... [
18]
DL | 1.27 × 10-2 mm2·s-1 [18] | | β | 1[18] | ∆v/VA | 0.2826[4] |
| α | 6[18] | a | 2.8665 × 10-7 mm[13] |
<strong>3</strong> 结果与讨论<strong>3.1</strong> 扩散速度对氢浓度动态演化的影响鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... -1 [
18]
| β | 1[18] | ∆v/VA | 0.2826[4] |
| α | 6[18] | a | 2.8665 × 10-7 mm[13] |
<strong>3</strong> 结果与讨论<strong>3.1</strong> 扩散速度对氢浓度动态演化的影响鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... [
18]
∆v/VA | 0.2826[4] | | α | 6[18] | a | 2.8665 × 10-7 mm[13] |
<strong>3</strong> 结果与讨论<strong>3.1</strong> 扩散速度对氢浓度动态演化的影响鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... [
18]
a | 2.8665 × 10-7 mm[13] | <strong>3</strong> 结果与讨论<strong>3.1</strong> 扩散速度对氢浓度动态演化的影响鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... 鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
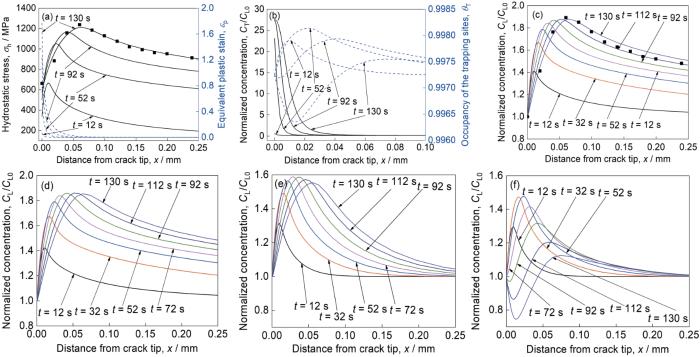
... 图3a给出低强度钢静水应力和塑性变形分布随加载时间的变化,可以看出随着加载时间增加静水应力的大小增加,位置内移且梯度降低,塑性变形由裂尖根部向内快速减小,但根部的最大值和塑性区尺寸随时间增加逐渐变大.图3c和d分别为快扩散速度下没有和有氢陷阱时NILS氢浓度在加载过程的变化,无论有没有考虑氢陷阱,与图3a对比可知NILS氢几乎同时紧跟静水应力的大小和位置变化形成氢浓度峰值.快扩散速度下使用的扩散模型和参数与文献[18]的研究一致,图3a和c中也给出了其静水应力和NILS氢浓度分布,比较可知本文的计算结果和文献[18]的计算结果较为接近.当扩散较慢时,如图3e和f所示,分别对应没有和有氢陷阱的情况.没有氢陷阱影响的计算结果表明氢仍能较快地紧跟静水应力的变化在静水应力高的地方聚集,但是同一时间内,氢浓度(与快扩散速度情况下相比)低15%左右;当考虑氢陷阱时,尽管加载的前期NILS氢也能够跟随静水应力变化而变化,但是总体浓度比无氢陷阱低,而随着加载的继续,NILS氢浓度分布逐渐在靠近裂尖根部形成浓度低谷(低于表面氢浓度),在静水应力峰值位置仍有浓度峰,但较平缓且水平比无氢陷阱时低得多.慢扩散时陷阱氢浓度和氢陷阱的饱和程度(占据率)如图3b所示,说明陷阱氢主要分布在裂尖根部附近的塑性区内且同一位置随时间变化先快速增加后趋于稳定,其值是NILS氢浓度的几十倍;再看氢陷阱饱和度虽然跟随NILS氢浓度变化但是一直保持在99.6%以上,这表明氢陷阱浓度几乎和NILS氢浓度无关,这是因为氢陷阱激活能高达60 kJ/mol使得其常温陷阱饱和度几乎与NILS氢浓度无关.不同扩散速度时有无氢陷阱的氢浓度分布的差别可以使用图3b来解释:由于高的陷阱激活能使得新产生的氢陷阱必须消耗附近的NILS氢来填满陷阱位置,快扩散速度使得在静水应力梯度驱动下被消耗NILS氢立即从基体内部和外界获得补充,慢的扩散速度则无法及时获得补充.这种情况说明裂尖氢浓度在动态加载时不仅与加载速度有关[19],而且跟扩散速度有很大的关系,扩散速度越慢,不仅将导致氢在静水应力高的地方聚集时间增加,而且同时由于氢陷阱的作用会使得峰值浓度更低且裂尖附近塑性区的NILS氢含量大大下降并延缓氢在高静水拉应力附近的聚集. ...
... 中也给出了其静水应力和NILS氢浓度分布,比较可知本文的计算结果和文献[18]的计算结果较为接近.当扩散较慢时,如图3e和f所示,分别对应没有和有氢陷阱的情况.没有氢陷阱影响的计算结果表明氢仍能较快地紧跟静水应力的变化在静水应力高的地方聚集,但是同一时间内,氢浓度(与快扩散速度情况下相比)低15%左右;当考虑氢陷阱时,尽管加载的前期NILS氢也能够跟随静水应力变化而变化,但是总体浓度比无氢陷阱低,而随着加载的继续,NILS氢浓度分布逐渐在靠近裂尖根部形成浓度低谷(低于表面氢浓度),在静水应力峰值位置仍有浓度峰,但较平缓且水平比无氢陷阱时低得多.慢扩散时陷阱氢浓度和氢陷阱的饱和程度(占据率)如图3b所示,说明陷阱氢主要分布在裂尖根部附近的塑性区内且同一位置随时间变化先快速增加后趋于稳定,其值是NILS氢浓度的几十倍;再看氢陷阱饱和度虽然跟随NILS氢浓度变化但是一直保持在99.6%以上,这表明氢陷阱浓度几乎和NILS氢浓度无关,这是因为氢陷阱激活能高达60 kJ/mol使得其常温陷阱饱和度几乎与NILS氢浓度无关.不同扩散速度时有无氢陷阱的氢浓度分布的差别可以使用图3b来解释:由于高的陷阱激活能使得新产生的氢陷阱必须消耗附近的NILS氢来填满陷阱位置,快扩散速度使得在静水应力梯度驱动下被消耗NILS氢立即从基体内部和外界获得补充,慢的扩散速度则无法及时获得补充.这种情况说明裂尖氢浓度在动态加载时不仅与加载速度有关[19],而且跟扩散速度有很大的关系,扩散速度越慢,不仅将导致氢在静水应力高的地方聚集时间增加,而且同时由于氢陷阱的作用会使得峰值浓度更低且裂尖附近塑性区的NILS氢含量大大下降并延缓氢在高静水拉应力附近的聚集. ...
Hydrogen transport near a blunting crack tip
5
1999
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 本文采用的氢扩散模型是基于Krom等[19]的研究,同时考虑氢致局部软化效应和氢致晶格膨胀.该模型可分为扩散和弹塑性有限变形两部分.扩散部分基于LEM理论,同时考虑应力诱导扩散和应变对氢陷阱的影响.弹塑性有限变形计算基于各向同性硬化和Von-Mises J2流动法则. ...
... 式(7)中DL为晶格扩散常数,VH为氢的偏摩尔体积,σh = (σxx + σyy + σzz)/3为静水应力,∇为Hamilton算子.氢在氢陷阱的浓度变化率要同时考虑NILS氢浓度和陷阱数量随塑性变形的变化[19],故由微分链式法则有: ...
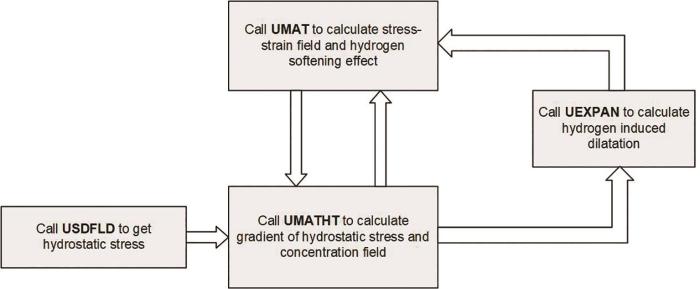
... 氢扩散是一个包含传质和力学响应的实时交互过程,所以其实现过程可分为两部分:扩散部分和弹塑性变形部分.有限元软件如Abaqus[33,36,37]或者MSC.MARC[19]的温度应力模块提供的二次开发接口可以实现本文的氢扩散模型而无需从头编制求解程序,本文采用Abaqus软件作为实现载体.扩散部分与传热过程类似,表1比较了传热和扩散的主要特征,可以发现两者在控制方程、传递质量或热量的规律和物理量等方面极为相似,都遵循守恒定律.由于Aabqus中传质模块不提供二次开发接口[38],考虑传热与传质的相似性,故可以使用Abaqus中提供的传热模块的子程序实现氢扩散.对于弹塑性部分可以使用UMAT接口实现氢致软化效应,使用UEXPAN定义氢致膨胀效应.扩散部分和弹塑性部分间的耦合响应可以借助Aabqus中Full Couple Temperature-Displacement模块提供的耦合求解器求解. ...
... 图3a给出低强度钢静水应力和塑性变形分布随加载时间的变化,可以看出随着加载时间增加静水应力的大小增加,位置内移且梯度降低,塑性变形由裂尖根部向内快速减小,但根部的最大值和塑性区尺寸随时间增加逐渐变大.图3c和d分别为快扩散速度下没有和有氢陷阱时NILS氢浓度在加载过程的变化,无论有没有考虑氢陷阱,与图3a对比可知NILS氢几乎同时紧跟静水应力的大小和位置变化形成氢浓度峰值.快扩散速度下使用的扩散模型和参数与文献[18]的研究一致,图3a和c中也给出了其静水应力和NILS氢浓度分布,比较可知本文的计算结果和文献[18]的计算结果较为接近.当扩散较慢时,如图3e和f所示,分别对应没有和有氢陷阱的情况.没有氢陷阱影响的计算结果表明氢仍能较快地紧跟静水应力的变化在静水应力高的地方聚集,但是同一时间内,氢浓度(与快扩散速度情况下相比)低15%左右;当考虑氢陷阱时,尽管加载的前期NILS氢也能够跟随静水应力变化而变化,但是总体浓度比无氢陷阱低,而随着加载的继续,NILS氢浓度分布逐渐在靠近裂尖根部形成浓度低谷(低于表面氢浓度),在静水应力峰值位置仍有浓度峰,但较平缓且水平比无氢陷阱时低得多.慢扩散时陷阱氢浓度和氢陷阱的饱和程度(占据率)如图3b所示,说明陷阱氢主要分布在裂尖根部附近的塑性区内且同一位置随时间变化先快速增加后趋于稳定,其值是NILS氢浓度的几十倍;再看氢陷阱饱和度虽然跟随NILS氢浓度变化但是一直保持在99.6%以上,这表明氢陷阱浓度几乎和NILS氢浓度无关,这是因为氢陷阱激活能高达60 kJ/mol使得其常温陷阱饱和度几乎与NILS氢浓度无关.不同扩散速度时有无氢陷阱的氢浓度分布的差别可以使用图3b来解释:由于高的陷阱激活能使得新产生的氢陷阱必须消耗附近的NILS氢来填满陷阱位置,快扩散速度使得在静水应力梯度驱动下被消耗NILS氢立即从基体内部和外界获得补充,慢的扩散速度则无法及时获得补充.这种情况说明裂尖氢浓度在动态加载时不仅与加载速度有关[19],而且跟扩散速度有很大的关系,扩散速度越慢,不仅将导致氢在静水应力高的地方聚集时间增加,而且同时由于氢陷阱的作用会使得峰值浓度更低且裂尖附近塑性区的NILS氢含量大大下降并延缓氢在高静水拉应力附近的聚集. ...
Distribution of hydrogen concentration near notch tip under mode I loading
1
1990
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
I型载荷下缺口前端氢浓度分布的研究
1
1990
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
Mechanics and thermodynamics on the stress and hydrogen interaction in crack tip stress corrosion: experiment and theory
1
1998
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
Investigation of deformation field and hydrogen partition around crack tip in fcc single crystal
1
1995
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
An example of the effect of hydrogen trapping on hydrogen embrittlement
1
1981
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
Hydrogen trap states in ultrahigh-strength AERMET 100 steel
5
2004
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... 陷阱激活能和陷阱密度是表征氢陷阱的主要参数,然而对于位错氢陷阱的激活能,不同文献报道的值相差较大[24,25,32,41,42].Pressouyre[43]认为位错陷阱的平均激活能在28.6~35.5 kJ/mol之间.Oriani[17]利用电化学渗透法测出位错陷阱的激活能为27.6 kJ/mol.Kumnick和Johnson[31]通过冷轧形变的纯铁的电化学渗透则给出60 kJ/mol的值,他们推测对应的陷阱可能为位错核及割阶.Hirth[41]分析了以上数据后认为60 kJ/mol的激活能对应于混合位错核及刃型位错核,而20~30 kJ/mol的激活能则对应螺型位错核,0~20 kJ/mol对应位错的弹性应力场.Taketomi等[42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
... [24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
... 由以上计算结果可知,氢陷阱的激活能对氢浓度分布具有决定性的影响,因此精确鉴别氢陷阱类型、测定结合能和陷阱密度十分重要[13].本文只考虑到单一陷阱模型,实际上金属内存在多种陷阱都有可能对氢脆产生重要影响,例如Li等[24]在研究AERMET 100钢中氢陷阱对氢脆机制的作用时发现被M2C碳化物捕获的氢会导致碳化物颗粒附近的基体发生解理开裂,而Novak等[25]则认为位错氢陷阱是AISI 4130钢氢脆的主要原因. ...
A statistical, physical-based, micro-mechanical model of hydrogen-induced intergranular fracture in steel
4
2010
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 以上分析表明对于低强度钢,即使初始NILS氢浓度很高其稳态浓度分布仍由氢陷阱控制,而对于高强度钢,在初始浓度高于4.24 × 10-9时可以采用无氢陷阱模型计算,如果进一步考虑到高强度钢裂尖或者缺口的塑性应变通常较低[4],则无氢陷阱的模型的使用范围将扩大.稳态氢浓度分布通常与氢致滞后断裂有关[29,30].Wang等[30]研究了AISI4130高强度钢缺口试样在初始氢浓度为6 × 10-8~3 × 10-7 (质量分数)的氢致滞后断裂,采用无氢陷阱模型计算氢扩散并对比实验结果,表明计算结果与实验吻合程度较好,对比本文计算的浓度范围可知其计算结果与本文符合.中低强度钢的裂尖和缺口根部附近不仅有较大的塑性变形同时也存在高的氢浓度,其裂纹易在此范围内萌生.如Olden等[28]研究了屈服强度为600 MPa的25%Cr双相不锈钢的氢致滞后断裂发现裂纹在缺口根部和近缺口处的铁素体相形核而并非静水应力最大处.对高强钢,裂尖或者缺口的塑性变形量较小,但其静水应力却很大,故裂纹易在静水应力附近形核,如Novak等[25]在研究AISI4130高强钢四点弯缺口试样在79 MPa氢气中热充氢后的氢致滞后断裂时表明裂纹在最大静水应力处附近萌生. ...
... 陷阱激活能和陷阱密度是表征氢陷阱的主要参数,然而对于位错氢陷阱的激活能,不同文献报道的值相差较大[24,25,32,41,42].Pressouyre[43]认为位错陷阱的平均激活能在28.6~35.5 kJ/mol之间.Oriani[17]利用电化学渗透法测出位错陷阱的激活能为27.6 kJ/mol.Kumnick和Johnson[31]通过冷轧形变的纯铁的电化学渗透则给出60 kJ/mol的值,他们推测对应的陷阱可能为位错核及割阶.Hirth[41]分析了以上数据后认为60 kJ/mol的激活能对应于混合位错核及刃型位错核,而20~30 kJ/mol的激活能则对应螺型位错核,0~20 kJ/mol对应位错的弹性应力场.Taketomi等[42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
... 由以上计算结果可知,氢陷阱的激活能对氢浓度分布具有决定性的影响,因此精确鉴别氢陷阱类型、测定结合能和陷阱密度十分重要[13].本文只考虑到单一陷阱模型,实际上金属内存在多种陷阱都有可能对氢脆产生重要影响,例如Li等[24]在研究AERMET 100钢中氢陷阱对氢脆机制的作用时发现被M2C碳化物捕获的氢会导致碳化物颗粒附近的基体发生解理开裂,而Novak等[25]则认为位错氢陷阱是AISI 4130钢氢脆的主要原因. ...
Dependence of hydrogen-induced lattice defects and hydrogen embrittlement of cold-drawn pearlitic steels on hydrogen trap state, temperature, strain rate and hydrogen content
2
2014
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 陷阱激活能和陷阱密度是表征氢陷阱的主要参数,然而对于位错氢陷阱的激活能,不同文献报道的值相差较大[24,25,32,41,42].Pressouyre[43]认为位错陷阱的平均激活能在28.6~35.5 kJ/mol之间.Oriani[17]利用电化学渗透法测出位错陷阱的激活能为27.6 kJ/mol.Kumnick和Johnson[31]通过冷轧形变的纯铁的电化学渗透则给出60 kJ/mol的值,他们推测对应的陷阱可能为位错核及割阶.Hirth[41]分析了以上数据后认为60 kJ/mol的激活能对应于混合位错核及刃型位错核,而20~30 kJ/mol的激活能则对应螺型位错核,0~20 kJ/mol对应位错的弹性应力场.Taketomi等[42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
A quantum-mechanically informed continuum model of hydrogen embrittlement
4
2004
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... [27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
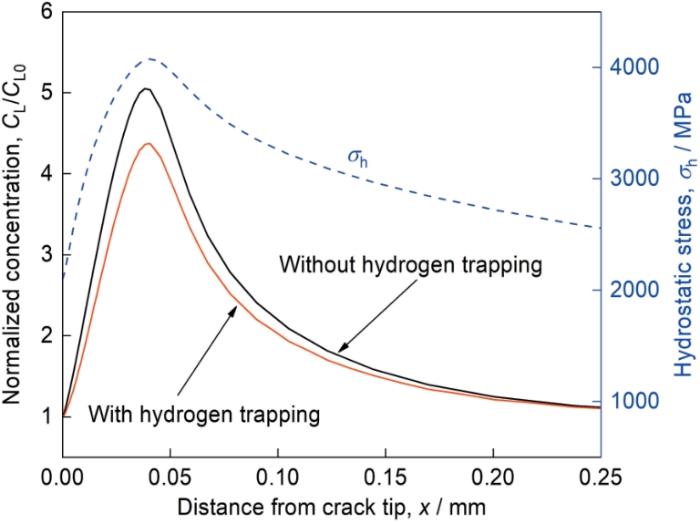
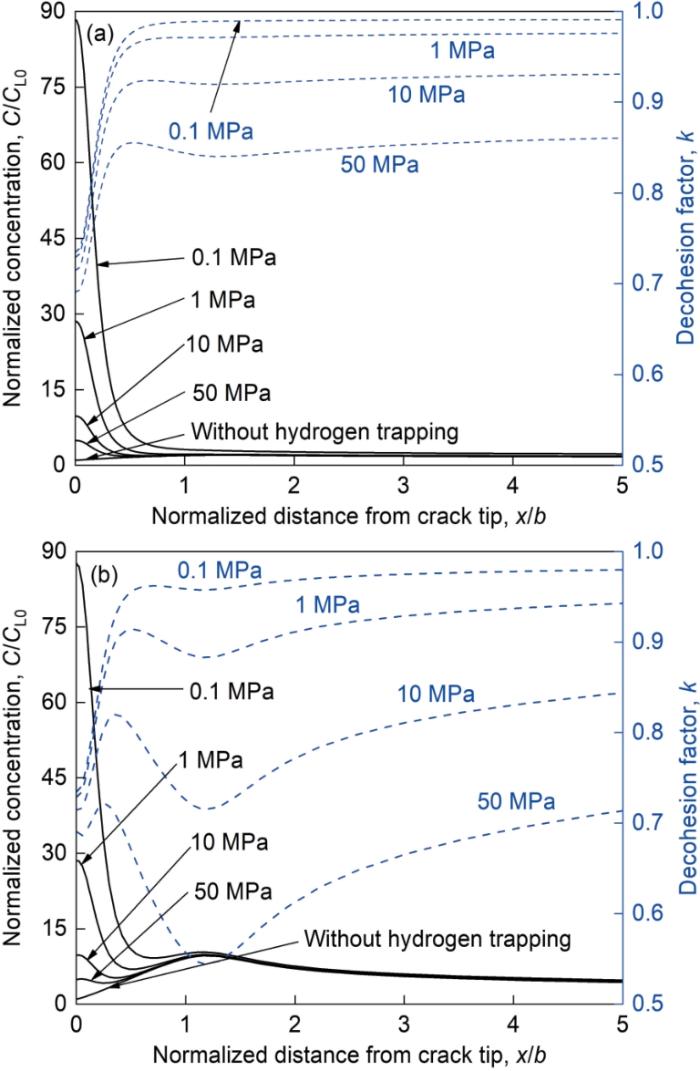
... 为了考察初始氢浓度对氢扩散的影响,本文选取0.1~50 MPa的初始环境氢活度进行研究,根据 式(16)得对应的初始NILS氢浓度CL0范围是4.2 × 10-10~9.5 × 10-9 (质量分数,下同).第一性原理计算表明氢会降低Fe和bcc钢的原子键合力,降低的程度与氢覆盖率θ有关[27],如 式(18)所示,k表示存在氢时的原子键合力与无氢时的比值.Serebrinsky等[27]建议采用Langmuir-McLean等温方程关联氢浓度与氢覆盖率,即 式(19),其中∆g为氢与材料表面的界面结合能,对于bcc钢取30 kJ/mol.稳态氢浓度分布和k值结果如图5所示,两种强度的钢的总氢浓度(C = CL + CT)与初始NILS氢浓度CL0之比均随着初始浓度升高而降低,对低强度钢总氢浓度一直由氢陷阱浓度所主导,而高强度钢则逐步变为静水应力主导.这种现象也反映在原子键合力降低的程度上,低强度钢的原子键合力下降最大的部位始终在裂尖根部附近,但是高强度钢则随初始氢浓度增加其原子键合力最低的位置由裂尖根部逐渐变为静水应力峰值位置. ...
... [27]建议采用Langmuir-McLean等温方程关联氢浓度与氢覆盖率,即 式(19),其中∆g为氢与材料表面的界面结合能,对于bcc钢取30 kJ/mol.稳态氢浓度分布和k值结果如图5所示,两种强度的钢的总氢浓度(C = CL + CT)与初始NILS氢浓度CL0之比均随着初始浓度升高而降低,对低强度钢总氢浓度一直由氢陷阱浓度所主导,而高强度钢则逐步变为静水应力主导.这种现象也反映在原子键合力降低的程度上,低强度钢的原子键合力下降最大的部位始终在裂尖根部附近,但是高强度钢则随初始氢浓度增加其原子键合力最低的位置由裂尖根部逐渐变为静水应力峰值位置. ...
Influence of hydrogen from cathodic protection on the fracture susceptibility of 25%Cr duplex stainless steel-Constant load SENT testing and FE-modelling using hydrogen influenced cohesive zone elements
2
2009
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 以上分析表明对于低强度钢,即使初始NILS氢浓度很高其稳态浓度分布仍由氢陷阱控制,而对于高强度钢,在初始浓度高于4.24 × 10-9时可以采用无氢陷阱模型计算,如果进一步考虑到高强度钢裂尖或者缺口的塑性应变通常较低[4],则无氢陷阱的模型的使用范围将扩大.稳态氢浓度分布通常与氢致滞后断裂有关[29,30].Wang等[30]研究了AISI4130高强度钢缺口试样在初始氢浓度为6 × 10-8~3 × 10-7 (质量分数)的氢致滞后断裂,采用无氢陷阱模型计算氢扩散并对比实验结果,表明计算结果与实验吻合程度较好,对比本文计算的浓度范围可知其计算结果与本文符合.中低强度钢的裂尖和缺口根部附近不仅有较大的塑性变形同时也存在高的氢浓度,其裂纹易在此范围内萌生.如Olden等[28]研究了屈服强度为600 MPa的25%Cr双相不锈钢的氢致滞后断裂发现裂纹在缺口根部和近缺口处的铁素体相形核而并非静水应力最大处.对高强钢,裂尖或者缺口的塑性变形量较小,但其静水应力却很大,故裂纹易在静水应力附近形核,如Novak等[25]在研究AISI4130高强钢四点弯缺口试样在79 MPa氢气中热充氢后的氢致滞后断裂时表明裂纹在最大静水应力处附近萌生. ...
Numerical simulation of hydrogen induced delayed fracture of AISI4135 high strength steel using cohesive zone modeling
2
2011
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 以上分析表明对于低强度钢,即使初始NILS氢浓度很高其稳态浓度分布仍由氢陷阱控制,而对于高强度钢,在初始浓度高于4.24 × 10-9时可以采用无氢陷阱模型计算,如果进一步考虑到高强度钢裂尖或者缺口的塑性应变通常较低[4],则无氢陷阱的模型的使用范围将扩大.稳态氢浓度分布通常与氢致滞后断裂有关[29,30].Wang等[30]研究了AISI4130高强度钢缺口试样在初始氢浓度为6 × 10-8~3 × 10-7 (质量分数)的氢致滞后断裂,采用无氢陷阱模型计算氢扩散并对比实验结果,表明计算结果与实验吻合程度较好,对比本文计算的浓度范围可知其计算结果与本文符合.中低强度钢的裂尖和缺口根部附近不仅有较大的塑性变形同时也存在高的氢浓度,其裂纹易在此范围内萌生.如Olden等[28]研究了屈服强度为600 MPa的25%Cr双相不锈钢的氢致滞后断裂发现裂纹在缺口根部和近缺口处的铁素体相形核而并非静水应力最大处.对高强钢,裂尖或者缺口的塑性变形量较小,但其静水应力却很大,故裂纹易在静水应力附近形核,如Novak等[25]在研究AISI4130高强钢四点弯缺口试样在79 MPa氢气中热充氢后的氢致滞后断裂时表明裂纹在最大静水应力处附近萌生. ...
基于内聚力模型的AISI4135高强钢氢致滞后断裂数值模拟
2
2011
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 以上分析表明对于低强度钢,即使初始NILS氢浓度很高其稳态浓度分布仍由氢陷阱控制,而对于高强度钢,在初始浓度高于4.24 × 10-9时可以采用无氢陷阱模型计算,如果进一步考虑到高强度钢裂尖或者缺口的塑性应变通常较低[4],则无氢陷阱的模型的使用范围将扩大.稳态氢浓度分布通常与氢致滞后断裂有关[29,30].Wang等[30]研究了AISI4130高强度钢缺口试样在初始氢浓度为6 × 10-8~3 × 10-7 (质量分数)的氢致滞后断裂,采用无氢陷阱模型计算氢扩散并对比实验结果,表明计算结果与实验吻合程度较好,对比本文计算的浓度范围可知其计算结果与本文符合.中低强度钢的裂尖和缺口根部附近不仅有较大的塑性变形同时也存在高的氢浓度,其裂纹易在此范围内萌生.如Olden等[28]研究了屈服强度为600 MPa的25%Cr双相不锈钢的氢致滞后断裂发现裂纹在缺口根部和近缺口处的铁素体相形核而并非静水应力最大处.对高强钢,裂尖或者缺口的塑性变形量较小,但其静水应力却很大,故裂纹易在静水应力附近形核,如Novak等[25]在研究AISI4130高强钢四点弯缺口试样在79 MPa氢气中热充氢后的氢致滞后断裂时表明裂纹在最大静水应力处附近萌生. ...
Determination of the critical hydrogen concentration for delayed fracture of high strength steel by constant load test and numerical calculation
4
2006
... 氢扩散的研究由来已久.早期使用经典Fick定律研究氢扩散[4,7,13],然而随着研究的深入Fick定律无法解释变形后钢的氢扩散通量降低现象.1948年Darken和Smith[14]首先提出氢陷阱的概念.氢陷阱(Hydrogen Traps,HT)是指,除了普通晶格间隙溶氢位置(Normal interstitial lattice sites,NILS)外,其他可溶解额外氢的晶体缺陷,如空位、杂质原子、位错、晶界、基体与第二相颗粒界面和孔洞等[8,13~15].1963年McNabb和Foster[16]根据实验现象首次提出考虑氢陷阱的非平衡氢扩散方程,但由于该方程参数难以测量且陷阱氢浓度与晶格氢浓度是隐性关系,导致该方程难以求解.在此基础上,Oriani[17]假设氢在NILS和氢陷阱间存在局部平衡(Local equilibrium model,LEM),得到了氢在陷阱中的浓度和NILS处氢浓度的显式关系.Sofronis和McMeeking[18]应用LEM理论并考虑静水应力的影响实现了裂纹尖端处氢扩散的模拟,之后Krom等[19]考虑了应变速率对氢扩散的影响.同一时期,吴世丁等[20]、Mao和Li[21]以及Sun等[22]利用离子探针研究裂纹尖端氢浓度分布发现裂尖前方有两个氢浓度峰,分别由塑性变形和高静水应力引起.Anand[5]在热动力学的框架下导出了大变形下考虑氢陷阱的氢扩散方程而构建氢扩散的热力学基础.氢陷阱除了影响氢扩散,在氢脆机制上也有重要作用[23].Li等[24]认为可逆氢陷阱可以作为局部裂纹萌发的氢源.Novak等[25]研究表明AISI4340钢的氢脆是由陷于位错中的氢控制而不是由碳化物界面和晶界处的氢控制.Doshida和Takai[26]研究表明陷于空位的氢增加了高强度珠光体钢的氢脆敏感性.然而不考虑氢陷阱的氢扩散模型也被常采用[27~30],如Serebrinsky等[27]、Olden等[28]和王艳飞等[29]采用应力诱导扩散计算出氢浓度并将其作为内聚力模型的变量研究氢环境下的裂纹扩展,研究表明所得结果与实验较一致.Wang等[30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... [30]认为高强度AISI4135钢缺口处的氢浓度主要由静水应力控制而不是由与塑性应变量有关的氢陷阱控制,据此他们也采用了只考虑应力诱导的氢扩散模型. ...
... 以上分析表明对于低强度钢,即使初始NILS氢浓度很高其稳态浓度分布仍由氢陷阱控制,而对于高强度钢,在初始浓度高于4.24 × 10-9时可以采用无氢陷阱模型计算,如果进一步考虑到高强度钢裂尖或者缺口的塑性应变通常较低[4],则无氢陷阱的模型的使用范围将扩大.稳态氢浓度分布通常与氢致滞后断裂有关[29,30].Wang等[30]研究了AISI4130高强度钢缺口试样在初始氢浓度为6 × 10-8~3 × 10-7 (质量分数)的氢致滞后断裂,采用无氢陷阱模型计算氢扩散并对比实验结果,表明计算结果与实验吻合程度较好,对比本文计算的浓度范围可知其计算结果与本文符合.中低强度钢的裂尖和缺口根部附近不仅有较大的塑性变形同时也存在高的氢浓度,其裂纹易在此范围内萌生.如Olden等[28]研究了屈服强度为600 MPa的25%Cr双相不锈钢的氢致滞后断裂发现裂纹在缺口根部和近缺口处的铁素体相形核而并非静水应力最大处.对高强钢,裂尖或者缺口的塑性变形量较小,但其静水应力却很大,故裂纹易在静水应力附近形核,如Novak等[25]在研究AISI4130高强钢四点弯缺口试样在79 MPa氢气中热充氢后的氢致滞后断裂时表明裂纹在最大静水应力处附近萌生. ...
... [30]研究了AISI4130高强度钢缺口试样在初始氢浓度为6 × 10-8~3 × 10-7 (质量分数)的氢致滞后断裂,采用无氢陷阱模型计算氢扩散并对比实验结果,表明计算结果与实验吻合程度较好,对比本文计算的浓度范围可知其计算结果与本文符合.中低强度钢的裂尖和缺口根部附近不仅有较大的塑性变形同时也存在高的氢浓度,其裂纹易在此范围内萌生.如Olden等[28]研究了屈服强度为600 MPa的25%Cr双相不锈钢的氢致滞后断裂发现裂纹在缺口根部和近缺口处的铁素体相形核而并非静水应力最大处.对高强钢,裂尖或者缺口的塑性变形量较小,但其静水应力却很大,故裂纹易在静水应力附近形核,如Novak等[25]在研究AISI4130高强钢四点弯缺口试样在79 MPa氢气中热充氢后的氢致滞后断裂时表明裂纹在最大静水应力处附近萌生. ...
Deep trapping states for hydrogen in deformed iron
6
1980
... 式中,β是平均每个溶剂原子对应的间隙位置数量;α是每个陷阱位置可容纳的氢原子数,用来描述氢陷阱的饱和性;θL和θT分别指氢占据的间隙位置和陷阱位置的比例(率).NL = NA/VM,NA = 6.023 × 1023 atoms·mol-1,为Avogadro常数,VM是溶剂金属的摩尔体积.氢陷阱密度与塑性变形量有关.Kumnick和Johnson[31]通过实验建立了纯铁中NT与等效塑性应变εp的关系,即 式(3).当无直接的NT实验数据时,通过假设位错线中每个原子平面含有一个陷阱位置,氢陷阱密度也可根据 式(4)由位错密度ρ估算[15,32],式中a为晶格常数. ...
... 上式表明氢浓度演化与塑性变形速率有关.其中,氢陷阱数量随塑性变形的变化关系由Kumnick和Johnson[31]的实验拟合给出.联立 式(1)与(2)和(5)~(8)并去掉积分符号,可得: ...
... 鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... 陷阱激活能和陷阱密度是表征氢陷阱的主要参数,然而对于位错氢陷阱的激活能,不同文献报道的值相差较大[24,25,32,41,42].Pressouyre[43]认为位错陷阱的平均激活能在28.6~35.5 kJ/mol之间.Oriani[17]利用电化学渗透法测出位错陷阱的激活能为27.6 kJ/mol.Kumnick和Johnson[31]通过冷轧形变的纯铁的电化学渗透则给出60 kJ/mol的值,他们推测对应的陷阱可能为位错核及割阶.Hirth[41]分析了以上数据后认为60 kJ/mol的激活能对应于混合位错核及刃型位错核,而20~30 kJ/mol的激活能则对应螺型位错核,0~20 kJ/mol对应位错的弹性应力场.Taketomi等[42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
... [31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
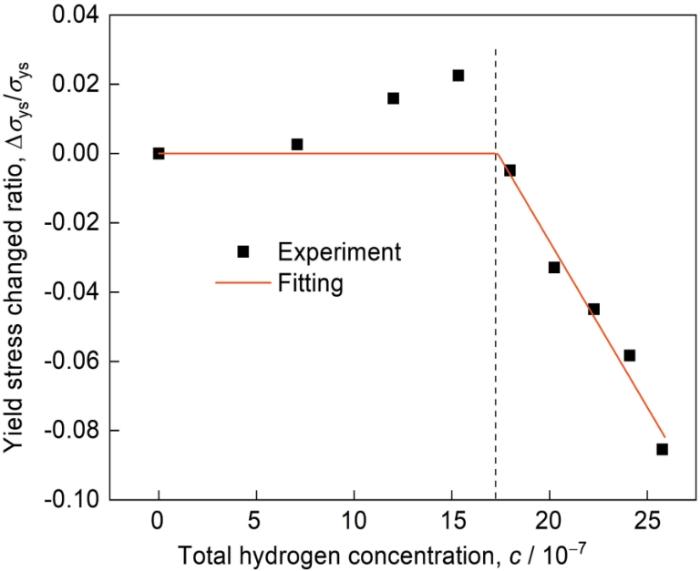
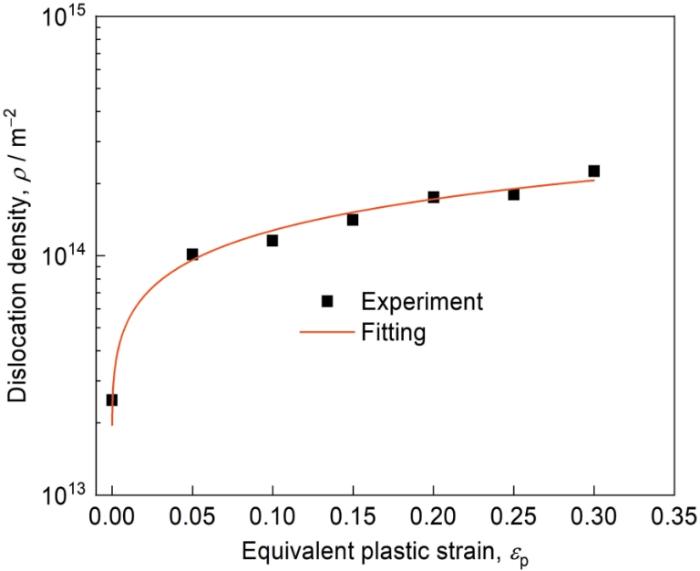
... 氢致软化和硬化存在一些争议,而最近研究表明这两种效应与氢和位错的相互作用有关[44]:随着氢浓度的增加,位错线附近被捕获的氢浓度增加,因位错拖拽氢导致的硬化受到了占据位错线的氢的屏蔽,将导致氢致硬化转为软化.这与Wang等[45]实验吻合:纯铁在氢含量低于3.21 × 10-7 (质量分数)时氢会导致微弱的硬化现象,而当氢含量大于3.57 × 10-7(质量分数)时则体现出明显的软化行为,如图7所示.通过拟合图7本文获得了氢致软化随浓度变化的关系,如 式(20)所示,由于氢致硬化现象极为微弱,故不考虑硬化效应,当总氢浓度大于3.09 × 10-7(质量分数)时氢致软化随氢浓度增加而线性增强,这与Sofronis等[35]建议的线性软化一致.同时本文根据Wang等[45]测得的位错密度用Taylor近似关系拟合其与塑性变形量的关系,如图8和 式(21)所示,说明在塑性变形的初始阶段,位错密度增加很快,之后缓慢增加,这与Kumnick和Johnson[31]的实验结果在数量级上一致且趋势也相同,Wang等[45]取氢陷阱结合能为30 kJ/mol.根据Wang等[45]的实验结果本节将只考虑纯铁的软化效应,取初始氢浓度为2.67 × 10-7(质量分数)以限制软化区域为裂尖附近. ...
A coupled diffusion and cohesive zone modelling approach for numerically assessing hydrogen embrittlement of steel structures
3
2017
... 式中,β是平均每个溶剂原子对应的间隙位置数量;α是每个陷阱位置可容纳的氢原子数,用来描述氢陷阱的饱和性;θL和θT分别指氢占据的间隙位置和陷阱位置的比例(率).NL = NA/VM,NA = 6.023 × 1023 atoms·mol-1,为Avogadro常数,VM是溶剂金属的摩尔体积.氢陷阱密度与塑性变形量有关.Kumnick和Johnson[31]通过实验建立了纯铁中NT与等效塑性应变εp的关系,即 式(3).当无直接的NT实验数据时,通过假设位错线中每个原子平面含有一个陷阱位置,氢陷阱密度也可根据 式(4)由位错密度ρ估算[15,32],式中a为晶格常数. ...
... 鉴于文献中报道的室温下铁和钢的氢扩散速度从1 × 10-2 mm2/s到1 × 10-6 mm2/s不等[24,32],为了研究扩散速度对氢扩散的影响,本文选取纯铁的扩散速度(1.27 × 10-2 mm2/s)作为快扩散速度及慢100倍的扩散速度(1.27 × 10-4 mm2/s)作为慢扩散速度进行研究,两种材料都置于1 MPa的氢气中,氢陷阱采用Kumnick和Johnson[31]的模型,其陷阱结合能WB = 60 kJ/mol.加载结束后低强度钢和高强度钢的裂尖张开位移分别为0.045和0.022 mm,裂尖根部的塑性变形分别为1.76和0.93,塑性区半径(εp > 10-3)分别为0.47和0.22 mm.相比于模型的尺寸,塑性区的尺寸要小两个数量级,依据Irwin的小范围屈服理论,当塑性区足够小时,远离屈服区的各点应力和位移可用基于弹性断裂力学的解来描述,因此采用 式(17)的弹性位移解作为模型的位移边界条件是合理的[18]. ...
... 陷阱激活能和陷阱密度是表征氢陷阱的主要参数,然而对于位错氢陷阱的激活能,不同文献报道的值相差较大[24,25,32,41,42].Pressouyre[43]认为位错陷阱的平均激活能在28.6~35.5 kJ/mol之间.Oriani[17]利用电化学渗透法测出位错陷阱的激活能为27.6 kJ/mol.Kumnick和Johnson[31]通过冷轧形变的纯铁的电化学渗透则给出60 kJ/mol的值,他们推测对应的陷阱可能为位错核及割阶.Hirth[41]分析了以上数据后认为60 kJ/mol的激活能对应于混合位错核及刃型位错核,而20~30 kJ/mol的激活能则对应螺型位错核,0~20 kJ/mol对应位错的弹性应力场.Taketomi等[42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
Coupled hydrogen diffusion simulation using a heat transfer analogy
2
2016
... 氢扩散驱动力为化学式梯度,不仅浓度会影响化学势,静水应力也会对化学势产生作用[18].同时考虑浓度梯度和静水应力梯度对扩散的驱动,且认为扩散通量仅由NILS中氢的扩散贡献,忽略陷阱之间的扩散[33],扩散通量为: ...
... 氢扩散是一个包含传质和力学响应的实时交互过程,所以其实现过程可分为两部分:扩散部分和弹塑性变形部分.有限元软件如Abaqus[33,36,37]或者MSC.MARC[19]的温度应力模块提供的二次开发接口可以实现本文的氢扩散模型而无需从头编制求解程序,本文采用Abaqus软件作为实现载体.扩散部分与传热过程类似,表1比较了传热和扩散的主要特征,可以发现两者在控制方程、传递质量或热量的规律和物理量等方面极为相似,都遵循守恒定律.由于Aabqus中传质模块不提供二次开发接口[38],考虑传热与传质的相似性,故可以使用Abaqus中提供的传热模块的子程序实现氢扩散.对于弹塑性部分可以使用UMAT接口实现氢致软化效应,使用UEXPAN定义氢致膨胀效应.扩散部分和弹塑性部分间的耦合响应可以借助Aabqus中Full Couple Temperature-Displacement模块提供的耦合求解器求解. ...
Lattice strains due to hydrogen in metals
1
1978
... 上式中顶标∇指Jaumann应力速率,G和v分别为剪切模量和Poisson比,δij 为Kronecker记号,Sij = σij -δijσh为应力偏量,σe = 3 Sij Sij /2为等效应力,h = dσe/dεp是单轴真应力和真塑性应变曲线的斜率,Dkl= D+ D+ D为总应变速率张量,D为氢致晶格膨胀贡献的变形速率,Peisl[34]假设氢致晶格膨胀为球对称的,并将名义体积应变转化为真应变,则有: ...
Hydrogen induced shear localization of the plastic flow in metals and alloys
5
2001
... 其中,Δv = VH/NA为金属中单个氢原子导致的平均体积应变,VA为单个金属原子占有平均体积.Sofronis等[35]通过在材料硬化模型中引入氢浓度来描述氢对屈服应力的影响,即: ...
... 式中,c为总氢的原子分数浓度;σ0为初始屈服应力;ε0为初始屈服应力对应的应变;n为硬化指数,假设其不受氢的影响[35];φ(c)为软/硬化系数,是c的函数,当0 < φ(c) < 1时表示软化,当φ(c) > 1时表示硬化.尽管HELP理论指出氢致软化是由于氢与位错的交互作用所致,引入 式(14)和(15)是为了能够以连续介质力学的角度考虑氢致软化问题而不是由其物理基础直接推导出[35],因此, 式(15)中的φ(c)一般根据实验现象拟合而得. ...
... [35],因此, 式(15)中的φ(c)一般根据实验现象拟合而得. ...
... 氢致软化和硬化存在一些争议,而最近研究表明这两种效应与氢和位错的相互作用有关[44]:随着氢浓度的增加,位错线附近被捕获的氢浓度增加,因位错拖拽氢导致的硬化受到了占据位错线的氢的屏蔽,将导致氢致硬化转为软化.这与Wang等[45]实验吻合:纯铁在氢含量低于3.21 × 10-7 (质量分数)时氢会导致微弱的硬化现象,而当氢含量大于3.57 × 10-7(质量分数)时则体现出明显的软化行为,如图7所示.通过拟合图7本文获得了氢致软化随浓度变化的关系,如 式(20)所示,由于氢致硬化现象极为微弱,故不考虑硬化效应,当总氢浓度大于3.09 × 10-7(质量分数)时氢致软化随氢浓度增加而线性增强,这与Sofronis等[35]建议的线性软化一致.同时本文根据Wang等[45]测得的位错密度用Taylor近似关系拟合其与塑性变形量的关系,如图8和 式(21)所示,说明在塑性变形的初始阶段,位错密度增加很快,之后缓慢增加,这与Kumnick和Johnson[31]的实验结果在数量级上一致且趋势也相同,Wang等[45]取氢陷阱结合能为30 kJ/mol.根据Wang等[45]的实验结果本节将只考虑纯铁的软化效应,取初始氢浓度为2.67 × 10-7(质量分数)以限制软化区域为裂尖附近. ...
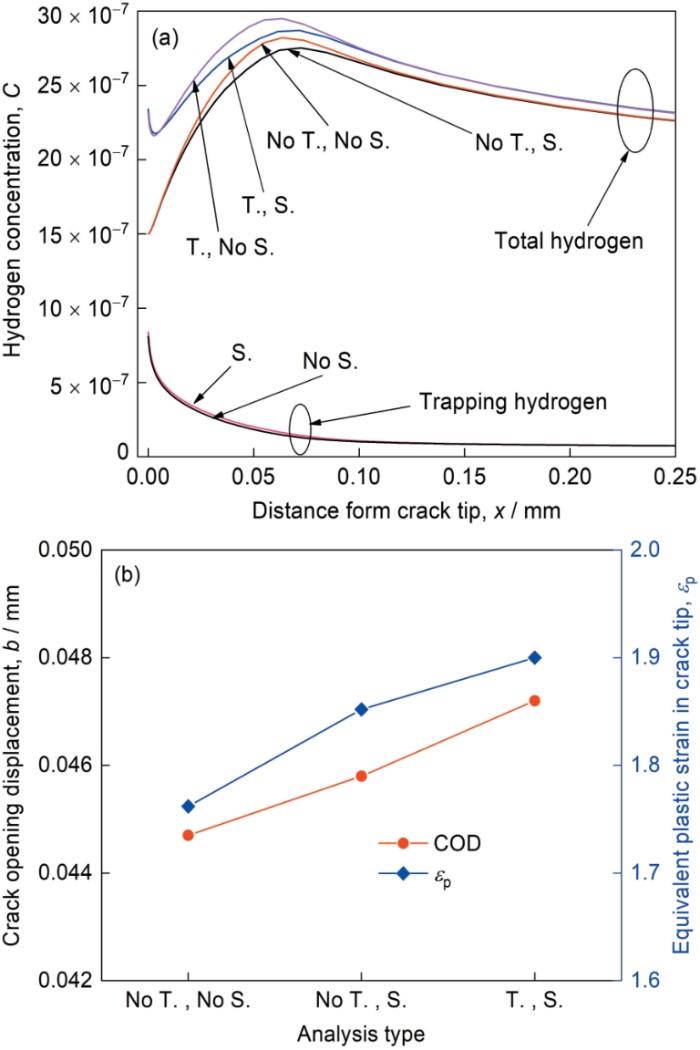
... 氢浓度分布如图10a所示,无论是否考虑氢陷阱,氢致软化都将导致氢浓度降低;但是考虑氢陷阱其静水应力附近的浓度降低较没有考虑氢陷阱的明显,同时在裂尖根部考虑软化作用的氢浓度比没有考虑软化作用的高,因为发生软化后,在同一应力强度因子下,裂尖附近的塑性变形量增加,提高了氢陷阱的密度,从而提升了裂尖附近的氢浓度,但由于使用的氢陷阱结合能较低,因此裂尖附近氢浓度的提升较小.进一步分析裂尖张开位移(COD)和裂尖根部等效塑性应变可以发现,如图10b所示,存在氢致软化时的COD和裂尖根部塑性应变量比没有考虑软化的高6%~8%,提升的数值并不大,从图9b可以看出这是因为本文考虑的初始氢浓度最高仅能导致11%的屈服应力的降低,而Sofronis等[35]指出氢致软化最高可以导致31%屈服应力的下降.考虑到COD是非线性的断裂参数,即使是微小的COD增加也可能会带来裂纹的扩展.此外氢与位错的相互作用是氢致软化或者硬化的本质,所以考虑氢致软化作用时必须采用有氢陷阱的扩散方程. ...
Numerical analysis of hydrogen transport using a hydrogen-enhanced localized plasticity mechanism
1
2012
... 氢扩散是一个包含传质和力学响应的实时交互过程,所以其实现过程可分为两部分:扩散部分和弹塑性变形部分.有限元软件如Abaqus[33,36,37]或者MSC.MARC[19]的温度应力模块提供的二次开发接口可以实现本文的氢扩散模型而无需从头编制求解程序,本文采用Abaqus软件作为实现载体.扩散部分与传热过程类似,表1比较了传热和扩散的主要特征,可以发现两者在控制方程、传递质量或热量的规律和物理量等方面极为相似,都遵循守恒定律.由于Aabqus中传质模块不提供二次开发接口[38],考虑传热与传质的相似性,故可以使用Abaqus中提供的传热模块的子程序实现氢扩散.对于弹塑性部分可以使用UMAT接口实现氢致软化效应,使用UEXPAN定义氢致膨胀效应.扩散部分和弹塑性部分间的耦合响应可以借助Aabqus中Full Couple Temperature-Displacement模块提供的耦合求解器求解. ...
Coupled analysis of hydrogen transport using ABAQUS
1
2010
... 氢扩散是一个包含传质和力学响应的实时交互过程,所以其实现过程可分为两部分:扩散部分和弹塑性变形部分.有限元软件如Abaqus[33,36,37]或者MSC.MARC[19]的温度应力模块提供的二次开发接口可以实现本文的氢扩散模型而无需从头编制求解程序,本文采用Abaqus软件作为实现载体.扩散部分与传热过程类似,表1比较了传热和扩散的主要特征,可以发现两者在控制方程、传递质量或热量的规律和物理量等方面极为相似,都遵循守恒定律.由于Aabqus中传质模块不提供二次开发接口[38],考虑传热与传质的相似性,故可以使用Abaqus中提供的传热模块的子程序实现氢扩散.对于弹塑性部分可以使用UMAT接口实现氢致软化效应,使用UEXPAN定义氢致膨胀效应.扩散部分和弹塑性部分间的耦合响应可以借助Aabqus中Full Couple Temperature-Displacement模块提供的耦合求解器求解. ...
10-User Subroutines Reference Manual
1
6
... 氢扩散是一个包含传质和力学响应的实时交互过程,所以其实现过程可分为两部分:扩散部分和弹塑性变形部分.有限元软件如Abaqus[33,36,37]或者MSC.MARC[19]的温度应力模块提供的二次开发接口可以实现本文的氢扩散模型而无需从头编制求解程序,本文采用Abaqus软件作为实现载体.扩散部分与传热过程类似,表1比较了传热和扩散的主要特征,可以发现两者在控制方程、传递质量或热量的规律和物理量等方面极为相似,都遵循守恒定律.由于Aabqus中传质模块不提供二次开发接口[38],考虑传热与传质的相似性,故可以使用Abaqus中提供的传热模块的子程序实现氢扩散.对于弹塑性部分可以使用UMAT接口实现氢致软化效应,使用UEXPAN定义氢致膨胀效应.扩散部分和弹塑性部分间的耦合响应可以借助Aabqus中Full Couple Temperature-Displacement模块提供的耦合求解器求解. ...
Effect of transient trapping on hydrogen transport near a blunting crack tip
1
2021
... 其中,s为溶解度系数;p (MPa)为环境氢活度,近似等于环境氢压(当环境氢压较小时).由于本文研究对象为钢,不考虑钢中微量合金元素对溶解度系数的影响,s取为定值6.53 × 1012 atoms H·mm-3·MPa-1/2 [18].力学边界条件为裂纹对称线取对称边界条件,半圆弧处的位移边界条件使用I型裂纹弹性位移场以恒定应力强度因子加载130 s后保载1.3×104 s(由试算知该时间可以达到99%的稳态浓度分布),加载位移场和应力强度因子如 式(17)[39]: ...
On the synergy of diffusible hydrogen content and hydrogen diffusivity in the mechanical degradation of laboratory cast Fe-C alloys
2
2016
... 对于快扩散速度,尽管氢陷阱激活能高达60 kJ/mol,钢的强度对NILS氢的聚集几乎没有影响,如果只需要NILS氢浓度结果,则两种氢扩散模型均可;对于慢扩散速度,塑性区新产生的强陷阱将导致有氢陷阱的模型NILS氢浓度结果比无陷阱的低且浓度分布也不同,此效应对于低强度钢不可忽略,而对于高强度钢影响不大.可扩散氢即NILS氢在动态加载的HIC中起主要作用[40],以上计算结果表明无论有无氢陷阱,扩散速度越快则相同时间内NILS氢聚集在裂纹附近的浓度越高,则其HIC敏感性随着扩散速度增加而增加.Depover等[40]的实验便表明纯铁、马氏体和贝氏体钢预充氢缺口拉伸试样的HIC敏感性依次升高是由于扩散速度的增加导致的. ...
... [40]的实验便表明纯铁、马氏体和贝氏体钢预充氢缺口拉伸试样的HIC敏感性依次升高是由于扩散速度的增加导致的. ...
Effects of hydrogen on the properties of iron and steel
5
1980
... 陷阱激活能和陷阱密度是表征氢陷阱的主要参数,然而对于位错氢陷阱的激活能,不同文献报道的值相差较大[24,25,32,41,42].Pressouyre[43]认为位错陷阱的平均激活能在28.6~35.5 kJ/mol之间.Oriani[17]利用电化学渗透法测出位错陷阱的激活能为27.6 kJ/mol.Kumnick和Johnson[31]通过冷轧形变的纯铁的电化学渗透则给出60 kJ/mol的值,他们推测对应的陷阱可能为位错核及割阶.Hirth[41]分析了以上数据后认为60 kJ/mol的激活能对应于混合位错核及刃型位错核,而20~30 kJ/mol的激活能则对应螺型位错核,0~20 kJ/mol对应位错的弹性应力场.Taketomi等[42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
... [41]分析了以上数据后认为60 kJ/mol的激活能对应于混合位错核及刃型位错核,而20~30 kJ/mol的激活能则对应螺型位错核,0~20 kJ/mol对应位错的弹性应力场.Taketomi等[42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
... [41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
... [41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
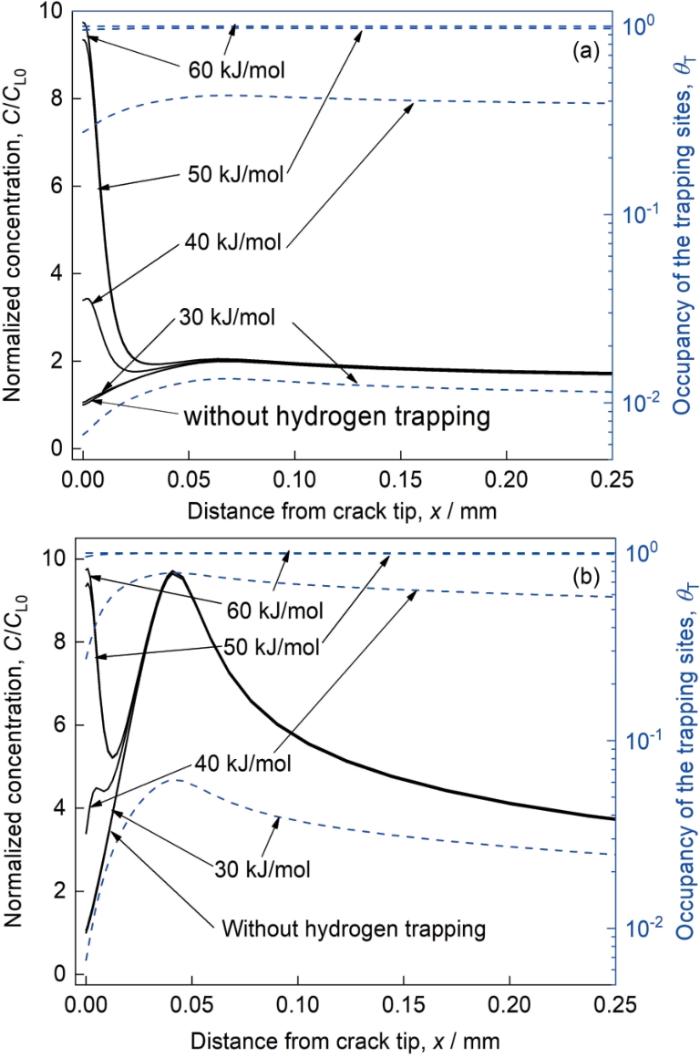
... 根据Hirth[41]的研究,20 kJ/mol的激活能只有在NILS氢浓度极高的情况下才需要考虑,而通常α-Fe的氢溶解度很低,故本文不考虑位错弹性场陷阱.为研究平均位错陷阱激活能对氢浓度演化的影响,根据以上分析选取30~60 kJ/mol的范围进行研究,初始氢环境氢压为10 MPa,陷阱密度采用 式(3)计算,结果如图6所示.首先可以发现对于低强度钢,当陷阱激活能小于30 kJ/mol时,含氢陷阱模型与只考虑静水应力结果几乎无差别;当陷阱激活能较高时,陷阱氢浓度处于主导地位,裂尖附近集聚的氢远高于静水应力峰值处集聚的氢.对于高强度钢只有在陷阱激活能高于40 kJ/mol时才能够对氢浓度分布产生影响,且其裂尖氢浓度与静水应力峰值附近氢浓度相当.这说明两种钢对于氢陷阱的敏感程度不同,低强度钢更易受到氢陷阱的影响.其次考察陷阱的氢占据率θT可以观察到,陷阱氢占据率随着激活能增加,在激活能较小时快速增加,激活能较大时则变化不大,其分布形状与NILS氢浓度分布形状类似,这可由 式(5)解释;当激活能高于50 kJ/mol时,两种钢中的氢陷阱几乎被饱和,而激活能为30 kJ/mol其陷阱占据率仅约为1%. ...
Atomistic study of hydrogen distribution and diffusion around a {112}<111> edge dislocation in alpha iron
2
2008
... 陷阱激活能和陷阱密度是表征氢陷阱的主要参数,然而对于位错氢陷阱的激活能,不同文献报道的值相差较大[24,25,32,41,42].Pressouyre[43]认为位错陷阱的平均激活能在28.6~35.5 kJ/mol之间.Oriani[17]利用电化学渗透法测出位错陷阱的激活能为27.6 kJ/mol.Kumnick和Johnson[31]通过冷轧形变的纯铁的电化学渗透则给出60 kJ/mol的值,他们推测对应的陷阱可能为位错核及割阶.Hirth[41]分析了以上数据后认为60 kJ/mol的激活能对应于混合位错核及刃型位错核,而20~30 kJ/mol的激活能则对应螺型位错核,0~20 kJ/mol对应位错的弹性应力场.Taketomi等[42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
... [42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
A classification of hydrogen traps in steel
1
1979
... 陷阱激活能和陷阱密度是表征氢陷阱的主要参数,然而对于位错氢陷阱的激活能,不同文献报道的值相差较大[24,25,32,41,42].Pressouyre[43]认为位错陷阱的平均激活能在28.6~35.5 kJ/mol之间.Oriani[17]利用电化学渗透法测出位错陷阱的激活能为27.6 kJ/mol.Kumnick和Johnson[31]通过冷轧形变的纯铁的电化学渗透则给出60 kJ/mol的值,他们推测对应的陷阱可能为位错核及割阶.Hirth[41]分析了以上数据后认为60 kJ/mol的激活能对应于混合位错核及刃型位错核,而20~30 kJ/mol的激活能则对应螺型位错核,0~20 kJ/mol对应位错的弹性应力场.Taketomi等[42]利用分子动力学计算了α-Fe{112}<111>位错的陷阱激活能,研究表明刃型位错核的激活能为42 kJ/mol,而其弹性应力场的激活能随着离位错核距离增大而变小,最大18 kJ/mol,这与Hirth[41]的推测结果类似.最近Doshida和Takai[26]测量珠光体钢的陷阱激活能时认为37 kJ/mol是位错核、渗碳体界面、空位和空位团激活能的平均值.综上所述,一方面氢陷阱的种类众多,其密度与激活能各不相同,而实验测量陷阱激活能是建立在单一陷阱理论的基础上,并未考虑多陷阱效应[41],故实验测量值一般为平均值;另一方面由于材料成分、热处理[24]和变形方式[31]的不同,其各种陷阱类型和比例也会有所区别,这就导致了实验测量平均值必然存在差异. ...
Solid solution softening and hardening by mobile solute atoms with special focus on hydrogen
1
2012
... 氢致软化和硬化存在一些争议,而最近研究表明这两种效应与氢和位错的相互作用有关[44]:随着氢浓度的增加,位错线附近被捕获的氢浓度增加,因位错拖拽氢导致的硬化受到了占据位错线的氢的屏蔽,将导致氢致硬化转为软化.这与Wang等[45]实验吻合:纯铁在氢含量低于3.21 × 10-7 (质量分数)时氢会导致微弱的硬化现象,而当氢含量大于3.57 × 10-7(质量分数)时则体现出明显的软化行为,如图7所示.通过拟合图7本文获得了氢致软化随浓度变化的关系,如 式(20)所示,由于氢致硬化现象极为微弱,故不考虑硬化效应,当总氢浓度大于3.09 × 10-7(质量分数)时氢致软化随氢浓度增加而线性增强,这与Sofronis等[35]建议的线性软化一致.同时本文根据Wang等[45]测得的位错密度用Taylor近似关系拟合其与塑性变形量的关系,如图8和 式(21)所示,说明在塑性变形的初始阶段,位错密度增加很快,之后缓慢增加,这与Kumnick和Johnson[31]的实验结果在数量级上一致且趋势也相同,Wang等[45]取氢陷阱结合能为30 kJ/mol.根据Wang等[45]的实验结果本节将只考虑纯铁的软化效应,取初始氢浓度为2.67 × 10-7(质量分数)以限制软化区域为裂尖附近. ...
Activation volume and density of mobile dislocations in hydrogen-charged iron
4
2013
... 氢致软化和硬化存在一些争议,而最近研究表明这两种效应与氢和位错的相互作用有关[44]:随着氢浓度的增加,位错线附近被捕获的氢浓度增加,因位错拖拽氢导致的硬化受到了占据位错线的氢的屏蔽,将导致氢致硬化转为软化.这与Wang等[45]实验吻合:纯铁在氢含量低于3.21 × 10-7 (质量分数)时氢会导致微弱的硬化现象,而当氢含量大于3.57 × 10-7(质量分数)时则体现出明显的软化行为,如图7所示.通过拟合图7本文获得了氢致软化随浓度变化的关系,如 式(20)所示,由于氢致硬化现象极为微弱,故不考虑硬化效应,当总氢浓度大于3.09 × 10-7(质量分数)时氢致软化随氢浓度增加而线性增强,这与Sofronis等[35]建议的线性软化一致.同时本文根据Wang等[45]测得的位错密度用Taylor近似关系拟合其与塑性变形量的关系,如图8和 式(21)所示,说明在塑性变形的初始阶段,位错密度增加很快,之后缓慢增加,这与Kumnick和Johnson[31]的实验结果在数量级上一致且趋势也相同,Wang等[45]取氢陷阱结合能为30 kJ/mol.根据Wang等[45]的实验结果本节将只考虑纯铁的软化效应,取初始氢浓度为2.67 × 10-7(质量分数)以限制软化区域为裂尖附近. ...
... [45]测得的位错密度用Taylor近似关系拟合其与塑性变形量的关系,如图8和 式(21)所示,说明在塑性变形的初始阶段,位错密度增加很快,之后缓慢增加,这与Kumnick和Johnson[31]的实验结果在数量级上一致且趋势也相同,Wang等[45]取氢陷阱结合能为30 kJ/mol.根据Wang等[45]的实验结果本节将只考虑纯铁的软化效应,取初始氢浓度为2.67 × 10-7(质量分数)以限制软化区域为裂尖附近. ...
... [45]取氢陷阱结合能为30 kJ/mol.根据Wang等[45]的实验结果本节将只考虑纯铁的软化效应,取初始氢浓度为2.67 × 10-7(质量分数)以限制软化区域为裂尖附近. ...
... [45]的实验结果本节将只考虑纯铁的软化效应,取初始氢浓度为2.67 × 10-7(质量分数)以限制软化区域为裂尖附近. ...