基于物理引导的集输管道内腐蚀速率预测及可解释性分析

doi:10.11902/1005.4537.2024.121

基于物理引导的集输管道内腐蚀速率预测及可解释性分析

陈潜¹, 黄伟^,¹, 张昌会², 管奥成¹, 张宸³, 叶晓芃⁴

1.长江大学石油工程学院武汉 430100

2.中国石油西南油气田分公司川中油气矿遂宁 629000

3.中国石油西南油气田分公司重庆气矿重庆 400707

4.中国西南油气田分公司川中北部采气管理处遂宁 629000

Physics-guided Prediction of Corrosion Rate Inside Gathering and Transportation Pipelines and Explanatory Analysis

CHEN Qian¹, HUANG Wei^,¹, ZHANG Changhui², GUAN Aocheng¹, ZHANG Chen³, YE Xiaopeng⁴

1.School of Petroleum Engineering, Yangtze University, Wuhan 430100, China

2.Central Sichuan Oil and Gas Mine, PetroChina Southwest Oil and Gas Field Company, Suining 629000, China

3.Chongqing Division, PetroChina Southwest Oil & Gasfield Company, Chongqing 400707, China

4.Central and Northern Sichuan Gas Production Management Office of Southwest Oil and Gas, Field Company, Suining 629000, China

通讯作者: 黄伟，E-mail：cjhuangwei@foxmail.com，研究方向为腐蚀信息化

收稿日期: 2024-04-12 修回日期: 2024-06-02

基金资助:

中国石油西南油气田公司博士后基金. 20220305-18

Corresponding authors: HUANG Wei, E-mail:cjhuangwei@foxmail.com

Received: 2024-04-12 Revised: 2024-06-02

作者简介 About authors

陈潜，男，1993年生，博士，讲师

摘要

由于恶劣的服役环境，集输管道的腐蚀问题愈发严重，亟需提出一种准确的模型来预测集输管道的内腐蚀速率。本文首先提出了一种基于物理引导神经网络(PGNN)与改进粒子群算法(IPSO)相结合的管道腐蚀预测方法。通过分析电化学腐蚀机理，总结不同腐蚀因素变化对腐蚀速率的普适性影响规律。然后基于这些普适性规律提出损失函数表征方法，构建物理引导的内腐蚀速率预测模型。使用改进粒子群算法优化模型的超参数。最后结合电化学腐蚀机理和部分依赖图、SHAP算法对预测模型进行可解释性分析。结果表明，PGNN-IPSO方法可以避免模型学习到与物理相悖的错误规律，提升模型预测准确度。该研究对集输管道的腐蚀防护、可靠性评估和维修决策具有重要意义。

关键词： 集输管道 ; 内腐蚀 ; 物理引导神经网络 ; 可解释性 ; 改进粒子群算法 ; SHAP算法 ; 部分依赖图

Abstract

Due to the harsh operating environment, the corrosion problem of gathering and transportation pipelines has become increasingly severe, necessitating the development of an accurate model to predict the internal corrosion rate of such pipelines. Herein, a pipeline corrosion prediction method that combines physics-guided neural networks (PGNN) with an improved particle swarm optimization (IPSO) algorithm is proposed. By analyzing the electrochemical corrosion mechanism, the universal impact of variations in different corrosion factors on the corrosion rate is summarized. Subsequently, based on these universal laws, a loss function characterization method is proposed to construct a physics-guided internal corrosion rate prediction model. The model's hyperparameters are optimized using a particle swarm algorithm improved through reverse learning, nonlinear weight adjustment mechanisms, and cosine algorithm enhancements. Finally, the predictive model is subjected to interpretability analysis using electrochemical corrosion mechanisms, partial dependence plots, and the SHAP algorithm. The accuracy of the model is evaluated using four metrics: mean absolute error (MAE), root mean square error (RMSE), mean absolute percentage error (MAPE), and R-squared (R²), while its reliability is assessed based on its consistency with corrosion mechanisms. Results demonstrate that the PGNN-IPSO method can avoid learning erroneous patterns contradicting physical principles, thereby enhancing prediction accuracy. This research holds significant implications for corrosion protection, reliability assessment, and maintenance decision-making regarding gathering and transportation pipelines.

Keywords： gathering pipeline ; internal corrosion ; physics-guided neural network ; interpretability analysis ; improved particle swarm optimization ; shapley additive explanations ; partial dependence plot

PDF (3780KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈潜, 黄伟, 张昌会, 管奥成, 张宸, 叶晓芃. 基于物理引导的集输管道内腐蚀速率预测及可解释性分析. 中国腐蚀与防护学报[J], 2025, 45(3): 720-730 DOI:10.11902/1005.4537.2024.121

CHEN Qian, HUANG Wei, ZHANG Changhui, GUAN Aocheng, ZHANG Chen, YE Xiaopeng. Physics-guided Prediction of Corrosion Rate Inside Gathering and Transportation Pipelines and Explanatory Analysis. Journal of Chinese Society for Corrosion and Protection[J], 2025, 45(3): 720-730 DOI:10.11902/1005.4537.2024.121

石油和天然气作为全球范围内至关重要的能源，在其输送方式中，管道运输被认为是最安全、经济的方法之一，被广泛应用于油气输送^[1]。然而，天然气和原油通常含有许多腐蚀性杂质，包括游离水、H₂S和CO₂等^[2~4]。这些杂质与管壁直接接触会引起管内壁腐蚀，严重时还会引发管道泄漏、破裂和断裂等事故，造成经济损失、环境破坏和人员伤亡等后果^[5~7]。准确评估管道腐蚀状况，进行预防性维护可以有效预防这些事故的发生^[8,9]。而管道腐蚀速率预测是评估其腐蚀状况的关键要素，对管道的风险评价和完整性管理具有重要意义^[10]。

传统的管道内腐蚀速率预测模型通常基于实验数据和腐蚀机理开发，这些模型大致可以分为3类：经验模型、半经验模型和机理模型^[1]。经验模型主要基于若干现场或实验数据进行回归或拟合得到，如挪威国家石油公司引入的Norsok M-506模型^[11,12]和Adams等^[13]提出的线性多元回归模型。相比于经验模型，半经验模型考虑了更广泛的因素和部分化学机制，如经过迭代改进以适应各种腐蚀影响因素的De Waard模型^[14~16]。而机理模型则是根据腐蚀电化学反应原理构建而成的。例如，NESIC等^[17]于1998年首创的电化学腐蚀机制模型及其后续迭代版本，如KSC模型等^[18~20]。这些模型影响机制清晰，可解释性强，被广泛应用于工程实际。但由于实际集输管道的腐蚀过程是多物理场作用耦合引起的，现有的大部分基于机理的管道内腐蚀预测模型未能充分考虑不同影响因素之间的促进或抑制作用，并且大多数模型采用参数化的近似方式来表征复杂的化学、电化学过程，因此往往与实际腐蚀过程存在一定偏差。

随着数据驱动方法的日益发展和成熟^[9,21,22]，近年来许多学者在管道腐蚀领域开展了基于数据驱动模型的预测方法研究^[23]。Xu等^[24]提出一种集成了完全集成经验模态分解与自适应噪声(CEEMDAN)和支持向量回归(SVR)的管道内腐蚀速率预测模型，并使用改进的粒子群优化算法(IPSO)进行超参数优化。Li等^[25]将核主成分分析(KPCA)和贝叶斯正则化人工神经网络相结合用于管道内腐蚀速率预测。Li等^[26]提出了一种融合主成分分析(PCA)、SVR和人工蜂群算法(ABC)的腐蚀速率预测方法。此外，Fang等^[27]应用随机森林(RF)和CatBoost两种集成学习算法(EL)对腐蚀速率进行预测，获得了较高准确度。这些研究在腐蚀速率预测方面取得了较好的应用效果。但为了获得强拟合能力，这些模型结构往往较为复杂，可解释能力差^[28~30]。同时，这些模型对腐蚀机理不可知，仅从训练数据中捕捉腐蚀规律，但由于管道内腐蚀数据集规模往往较小，数据驱动模型容易学习到与腐蚀机理相悖的错误规律，这些错误规律在该数据集上可能有较好表现，但外泛化性能差，难以指导实际的生产过程^[21,31~33]。

综上所述，现有内腐蚀速率预测模型的局限性可以概括为：(1) 机理驱动模型往往是在预设多个假设条件的理想情况下建模得到的，同时，也受到先验参数化的过度约束，因此与实际过程存在一定偏差，准确度有限。(2) 数据驱动模型为追求高准确度，往往具有复杂的结构，影响了其可解释性。(3) 复杂的数据驱动模型完全摒弃了腐蚀机理，可能会产生与物理相悖的结果，外泛化性能不足。

近年来许多学者试图将物理知识引入数据驱动模型，引导模型学习物理规律，以提高数据驱动模型的泛化能力和可解释性。物理知识可以通过多种方法与数据驱动模型相结合，例如将偏微分方程或常微分方程作为限制加入到数据驱动模型之中，使其训练得到的结果满足先验知识，从而构建物理信息神经网络(PINN)^[34~36]。但PINN在没有具体物理控制方程或控制方程不够精确的问题中适用性较为有限，因此学者们将更普适的定性规律融入数据驱动模型，构建了适用范围更广的物理引导神经网络(PGNN)。例如Daw等^[33]使用PGNN建立湖泊温度模型，其中添加了对温度，密度和水深之间定性关系的物理约束，以指导模型训练过程。Zhang等^[21]考虑中间变量影响建立PGNN对原油管道能耗进行预测。这些研究在物理知识与数据驱动模型相结合方面取得了较大的成果，但在集输管道内腐蚀速率预测方面暂无数据机理混合驱动模型的构建及应用，同时上述研究仍是基于预测误差对PGNN的有效性进行验证，但该方法无法有效验证物理规律的约束效果。

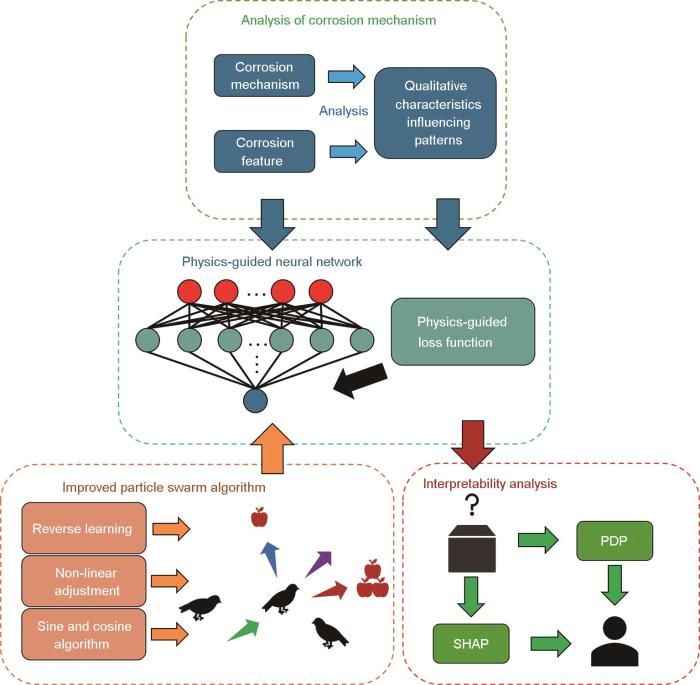
本文结合PGNN和IPSO构建管道腐蚀速率预测模型，通过多种可解释性方法定量分析了各腐蚀特征对腐蚀速率的影响。研究首先对腐蚀机制进行全面分析，得到各腐蚀特征对腐蚀速率影响的定性结论。随后，基于这些定性结论设计损失函数来构建PGNN，建立输入腐蚀特征变量与内腐蚀速率之间的映射关系。模型的超参数使用IPSO算法进行优化。最后，结合腐蚀电化学机理和部分依赖图、SHAP算法这些可解释性方法定量解析各个特征对内腐蚀速率的影响，在得到模型中各腐蚀因素对管道腐蚀速率作用机理的同时，证实了将腐蚀机制整合到神经网络模型训练过程中的有效性。本研究整体流程如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 总体框架图

Fig.1 Overall framework diagram

1 数据收集及分析

本研究收集了油气集输管道内腐蚀速率的数据集。该数据集包含从我国某地区集输管道中收集的200个样本。每组数据涵盖了6个影响腐蚀的特征，包括H₂S占比(X1)、CO₂占比(X2)、温度(X3)、pH(X4)、液体流速(X5)以及缓蚀剂注入量(X6)。

基于上述特征对集输管道内腐蚀规律进行分析，可知以下关系：(1) H₂S占比(X1)的增加会改变硫化物薄膜的组成，从FeS和FeS₂变为Fe₉S₈，增加了晶粒大小并削弱了阻止铁离子扩散的能力，从而提高腐蚀速率。(2) CO₂占比(X2)的增加会导致碳酸和氢离子浓度上升，进而使腐蚀速率增大。(3) 温度(X3)的升高加速了电化学和化学反应速率，从而提高腐蚀速率。然而，过高的温度可能影响溶解度并提高沉淀速率，有利于保护膜的形成，进而降低腐蚀速率。一般认为60~100 ℃间存在临界点，在温度低于该临界范围时，腐蚀速率随温度升高而增大，高于该临界点时随温度升高而下降。(4) pH (X4)与腐蚀速率成反比，即随着pH的升高，溶液中的氢离子浓度降低，腐蚀速率随之降低。(5) 较高的流速(X5)易冲刷破坏腐蚀产物形成的保护膜，导致腐蚀速率增大。(6) 随着缓蚀剂注入量(X6)的增加，腐蚀速率呈下降趋势。

表1展示了所收集数据集的描述性统计信息，定量描述了其中变量的分布特征。其中，变异系数用于衡量数据的离散程度，X6和V_corr较高的变异系数表明了缓蚀剂加注量和腐蚀速率分布的广泛性。峰度描述了数据分布的尖锐度或平坦度，V_corr较高的峰值表明腐蚀速率分布更尖锐。偏度反映了数据分布的对称性，X4和V_corr显著的偏度值表明pH值和腐蚀速率数据分布的不对称性。第5和第95百分位数(P5和P95)展示了各个特征的集中分布范围。

表1 采集数据的统计指标

Table 1 Statistical indicators of collected data

Feature	Mean	Min	Max	Std	Median	CV	Kurtosis	Skewness	P5	P95
X1 (%)	1.520	0.425	3.355	0.509	1.595	33.460	1.496	0.423	0.667	2.163
X2 (%)	2.476	0.514	6.774	0.943	2.579	38.067	4.731	1.161	1.000	3.472
X3 (℃)	39.075	20.820	59.423	8.693	38.636	22.246	0.044	0.302	24.329	56.052
X4	5.180	4.184	7.997	0.654	4.941	12.617	4.797	2.039	4.614	6.596
X5 (m/s)	1.937	0.592	2.967	0.483	1.964	24.923	0.193	-0.512	0.929	2.650
X6 (kg)	582.056	33.413	1474.000	364.668	497.383	62.652	-0.092	0.965	126.968	1304.858
V_corr (mm/a)	0.009	0.001	0.040	0.006	0.009	63.800	10.660	2.606	0.001	0.017

新窗口打开| 下载CSV

2 基础方法

2.1 预测模型

PGNN是一种融合传统机器学习算法与物理学原理的先进模型。它通过引入物理定律或已知的科学原理，提高了模型预测的准确性、可靠性和可解释性。PGNN主要通过在传统损失函数之外构建基于物理规律的损失项，使得模型在最小化预测值与真实值之间偏差的同时，保证其生成与物理规律一致的预测结果，实现模型预测准确性及物理一致性的双重保证。

通过第一节的分析可知，在数据集范围内，当其它特征不变时，若液体流速、CO₂占比、H₂S占比、温度(低于60 ℃)中任何一个特征增大，或者pH、缓蚀剂注入量、温度(高于100 ℃)中任何一个特征减小，都会导致腐蚀速率增大。为了确保数据模型学习到这一基于机理的知识，在预测模型训练的每个周期(epoch)中，当模型完成正常预测后，随机选择一个特征进行调整。若选择液体流速、CO₂占比、H₂S占比，则增大该特征值；若选择pH、缓蚀剂注入量，则减小该特征值；若选择温度，则增大其小于60 ℃的部分，减小其大于100 ℃的部分。使用调整后的特征进行二次预测。两次预测值应满足式(1)结果小于零，若其大于零，则式(1)被视为基于物理的损失项加入到损失函数(式(2))中。整体流程如图2所示。

Δ P H Y = \frac{1}{n} \sum_{i = 1}^{n} ({\hat{y}}_{i} - y_{i}^{'})

(1)

L o s s = \frac{1}{n} \sum_{i = 1}^{n} ({\hat{y}}_{i} - y_{i})^{2} + λ m a x (0, Δ P H Y)

(2)

式中，ΔPHY为物理差异项；n为样本总数； ${\hat{y}}_{i}$ 为模型在第i个样本上的预测值，y $_{i}^{'}$ 为模型在修改特征后的第i个样本上的预测值；y_i 为第i个样本的真实值；λ为物理损失项的权重。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 物理引导神经网络示意图

Fig.2 Schematic diagram of a physics-guided neural network

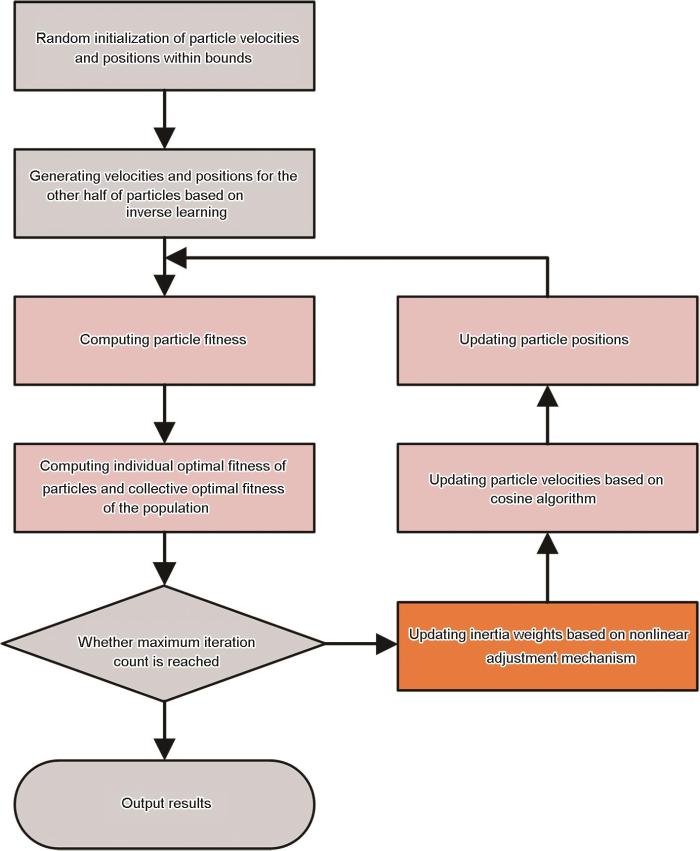
2.1.1 超参数优化

本研究中采用IPSO来解决PGNN模型的网络结构超参数优化问题。粒子群优化算法(PSO)作为一种先进的群体智能优化技术，通过模拟鸟类的集体觅食行为，寻找优化问题的最优解，具有较好的优化性能，但是也存在着难以兼顾全局搜索能力和收敛速度的缺点。基于此问题，本研究对PSO算法加以改进，提出兼顾这两者的IPSO算法。IPSO算法的关键改进处在于初始种群生成方式、动态调整的权重以及速度更新机制。采用反向学习生成方式来生成初始种群(式(3))，采用非线性调整机制来调整权重(式(4))，并采用正余弦算法来调整速度(式(6))，其流程图如图3所示。反向学习的初始种群生成方式可以有效增强初始种群的多样性，避免陷入局部最优解。引入正弦余弦因子后，学习因子的变化呈现一种震荡衰减性的搜索移动，震荡性搜索增加了粒子探索方向的多样性，拓宽了粒子的探索空间，而衰减性保证了算法的收敛速度。较大的惯性权重使算法全局搜索能力较强，较小的惯性权重则会增强算法的收敛速度，因此，非线性递减的惯性权重可以使算法在全局搜索能力和收敛速度上实现更好的平衡。在本研究中，以PGNN模型在测试集上的平均绝对百分比误差(MAPE)作为适应度函数，通过IPSO的迭代优化过程找到最佳的网络结构设置。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 改进粒子群算法流程图

Fig.3 Improved particle swarm algorithm flowchart

x_{j}^{'} = a_{j} + b_{j} - x_{j}

(3)

ω (t) = ω_{s t a r t} - (ω_{s t a r t} - ω_{e n d}) \times [\frac{2 t}{T_{m a x}} - {(\frac{t}{T_{m a x}})}^{2}]

(4)

r_{1} = 2 - 2 \times \frac{t}{T_{m a x}}

(5)

\{\begin{matrix} V_{i, j}^{t + 1} = ω (t) \times V_{i, j}^{t} + r_{1} \times s i n r_{2} \times (p b e s t_{i, j}^{t} - x_{i, j}^{t}) + \\ \begin{matrix} \begin{matrix} r_{1} \times s i n r_{2} \times (g b e s t_{j}^{t} - x_{i, j}^{t}) r_{3} < 0.5 \\ V_{i, j}^{t + 1} = ω (t) \times V_{i, j}^{t} + r_{1} \times c o s r_{2} \times (p b e s t_{i, j}^{t} - x_{i, j}^{t}) + \end{matrix} \\ r_{1} \times c o s r_{2} \times (g b e s t_{j}^{t} - x_{i, j}^{t}) r_{3} ⩾ 0.5 \end{matrix} \end{matrix}

(6)

式中，x $_{j}^{'}$ 为反向学习生成粒子的第j维的值；a_j 和b_j 分别为第j维的上下限；x_j 为随机生成粒子第j维的值；ω(t)为第t代时的惯性权重；ω_start为起始惯性权重；ω_end为最终惯性权重；t为当前迭代次数；T_max为最大迭代次数；x $_{i, j}^{t}$ 和V $_{i, j}^{t}$ 分别为t代第i个粒子在第j维的位置和速度分量；pbest $_{i, j}^{t}$ 为t代第i个粒子在第j维上的个体最优位置分量；gbest $_{j}^{t}$ 为t代整个种群在第j维上的最优位置分量；r₂为[0，2]间的随机数，与r₁(由式(5)计算)及r₃([0，1]间的随机数)一同辅助正余弦因子调整粒子速度。

2.1.2 模型性能评价指标

为了评估所提出模型的预测精度，本研究引入了平均绝对误差(MAE)、均方根误差(RMSE)、MAPE和决定系数(R²)来评估模型的预测性能。

M A E = \frac{1}{n} \sum_{i = 1}^{n} |y_{i} - {\hat{y}}_{i}|

(7)

R M S E = \sqrt[]{\frac{1}{n} \sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2}}

(8)

M A P E = \frac{1}{n} \sum_{i = 1}^{n} | \frac{y_{i} - {\hat{y}}_{i}}{y_{i}} | \times 100 %

(9)

R^{2} = 1 - \sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2} / \sum_{i = 1}^{n} (y_{i} {- \bar{y_{i}})}^{2}

(10)

式中，n为样本总数；y_i 为第i个样本的真实值； ${\hat{y}}_{i}$ 为第i个样本的预测值， $\bar{y_{i}}$ 为真实值的平均值。

2.2 模型可解释性分析

了解各腐蚀特征如何影响预测结果对于理解腐蚀预测模型的决策逻辑至关重要。这些结论一方面可以帮助衡量模型可信度，另一方面也可以为腐蚀防护提供有效理论支持。

本研究中，PDP被用来获得腐蚀速率预测结果随目标特征变化的变化趋势。它的核心思想是通过控制其它特征变量不变，计算目标特征对预测结果的边际贡献，其定义及计算方法如下：

{\hat{f}}_{x_{S}} (x_{S}) = E_{x_{C}} [{\hat{f}}_{x_{S}} (x_{S}, x_{C})] = \int {\hat{f}}_{x_{S}} (x_{S}, x_{C}) d P (x_{C})

(11)

{\hat{f}}_{x_{S}} (x_{S}) = \frac{1}{m} \sum_{i = 1}^{m} {\hat{f}}_{x_{S}} (x_{S}, x_{C}^{i})

(12)

式中，x_S为其部份依赖函数应被绘制的特征，x_C为在模型中使用的其它特征，m为特征总数。

SHAP算法被用来为模型预测提供更深入的解释，包括评估各特征的重要程度和解释各样本中的各个特征对预测结果的作用机制。SHAP算法将所有特征视为模型预测中的“贡献者”，对于每个样本，SHAP算法计算出每个特征对预测结果的贡献，该贡献即为该样本中该特征的SHAP值，平均绝对SHAP值反映了特征对预测影响的总体影响，因此它可以作为特征重要性的衡量标准。总体计算公式为：

β_{M} = \frac{| M |! (m - | M | - 1)!}{m!}

(13)

s h a p (x_{i, j}) = \sum_{M} β_{M} (y_{M \cup {x_{i, j}}} - y_{M})

(14)

y_{i} = y_{b a s e} + \sum_{j = 1}^{s} s h a p (x_{i, j})

(15)

α (x_{j}) = \frac{\sum_{i = 1}^{n} | s h a p (x_{i, j}) |}{n}

(16)

式中，β_M 为特征子集M的权重；M为不包括特征j的特征子集；m为特征数量；shap(x_i_,_j )为第i个样本的第j个特征的SHAP值；y_M 为模型在子集M下的预测值；y_i 为第i个样本的预测值；y_base为第i个样本预测值的期望值；α(x_j )为平均绝对SHAP值；n为样本总数。

3 结果与讨论

3.1 模型验证

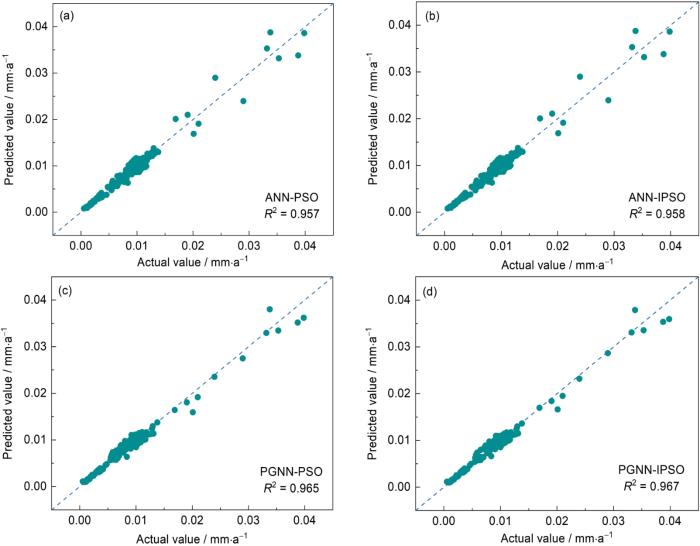
为了验证PGNN-IPSO模型的准确性，本研究将所提出的模型与改进前的模型进行比较，参与比较的模型包括ANN-PSO、ANN-IPSO、PGNN-PSO和PGNN-IPSO。采用五折交叉验证方法，以保证准确评估模型的预测性能，由于所有模型测试集均相同，图4展示了测试集上预测值相对于真实值的分布。各模型预测结果中均存在异常值，但相较于ANN，PGNN的异常值明显更少，且偏离程度更低，这可能是由于其具有腐蚀机理引导的原因。表2反映了该数据集上模型性能的差异。可以观察到，所提出的模型在预测性能方面显著优于其他模型，并且采用IPSO算法的模型比采用PSO算法的模型具有更高的预测精度。相较于其它3个模型，PGNN-IPSO模型的MAPE分别降低了0.5%、0.44%和0.03%。这表明引入物理规律引导可以有效提升模型捕捉腐蚀数据中复杂多元关系的能力，且IPSO算法具有更强的搜索性能。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 测试集上不同模型的预测结果

Fig.4 Results of different model predictions on the test set: (a) ANN-PSO, (b) ANN-IPSO, (c) PGNN-PSO, (d) PGNN-IPSO

表2 各模型误差

Table 2 Error of each model

Model	MAE / mm	RMSE / mm	MAPE / %	R²
ANN-PSO	0.000712	0.00106	7.71	0.957
ANN-IPSO	0.000706	0.00106	7.65	0.958
PGNN-PSO	0.000614	0.000897	7.24	0.965
PGNN-IPSO	0.000598	0.000865	7.21	0.967

新窗口打开| 下载CSV

3.2 模型解释和因素分析

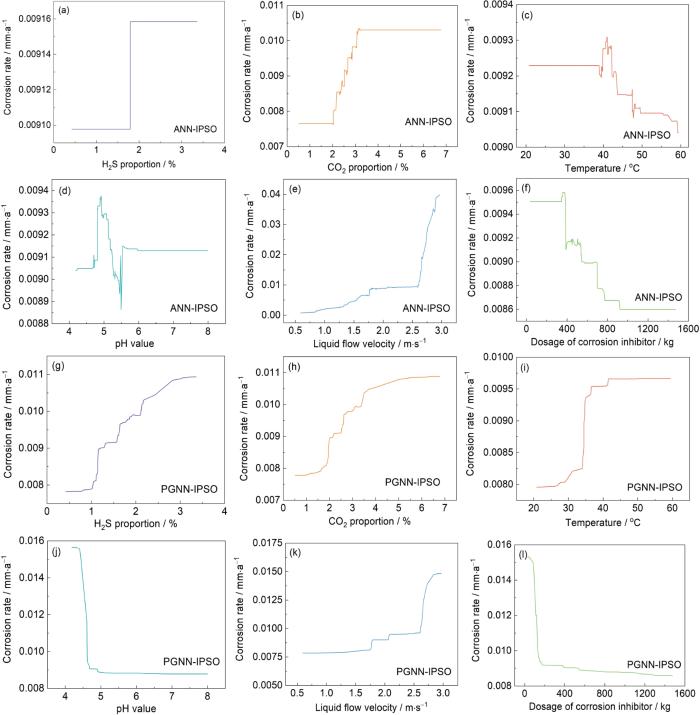
探索不同特征对预测结果的影响是理解模型的核心任务。图5展示了每个特征与管道腐蚀速率之间的关系。由图可知，未引入腐蚀机理的ANN-IPSO显示出的温度、pH等特征对腐蚀速率的影响呈复杂的非单调变化，表明模型学到了错误规律(与第1节的特征影响分析相悖)，导致实质上的过拟合。尽管在该数据集上误差较小，但外泛化能力差，难以获得信任，也无法用来分析腐蚀规律帮助腐蚀防护。相比之下，引入腐蚀机理的PGNN-IPSO模型清晰展现出各特征对腐蚀速率的影响，并与腐蚀机理相符。因此，其呈现的许多定量规律对于腐蚀防护具有较高的价值，下面进行详尽的分析。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 特征的部分依赖图

Fig.5 Partial dependence plot for the features: (a) H₂S proportion (ANN-IPSO), (b) CO₂ proportion (ANN-IPSO), (c) temperature (ANN-IPSO), (d) pH value (ANN-IPSO), (e) liquid flow velocity (ANN-IPSO), (f) dosage of corrosion inhibitor (ANN-IPSO), (g) H₂S proportion (PGNN-IPSO), (h) CO₂ proportion (PGNN-IPSO), (i) temperature(PGNN-IPSO), (j) pH value (PGNN-IPSO), (k) liquid flow velocity (PGNN-IPSO), (l) dosage of corrosion inhibitor (PGNN-IPSO)

CO₂占比是导致腐蚀的重要因素，先前的研究表明，当CO₂占比较小时，覆盖率较低，CO₂占比对腐蚀速率的影响不显著^[37]。随着CO₂占比增加，碳酸浓度增大导致阴极去极化反应速率加快，从而加速腐蚀，直到超过某一临界值时，形成致密的FeCO₃产物膜，阻止腐蚀继续加剧，使腐蚀速率趋于稳定^[38]。如图5所示，可以观察到CO₂占比对腐蚀速率的影响可分为3部分。首先，在CO₂占比达到2%之前，随着CO₂占比增加，腐蚀速率缓慢增加，表明此时CO₂占比尚未达到临界水平。当CO₂占比超过2%时，管道腐蚀速率急剧增加，但在CO₂占比达到4%时减缓，此时开始形成稳定且致密的FeCO₃钝化膜。这验证了经腐蚀机理引导的PGNN-IPSO模型成功地学习到了管道腐蚀速率受CO₂占比影响的规律。

温度对腐蚀的影响机制非常复杂，可视为腐蚀反应的活化能、成膜机制、pH和H₂S/CO₂溶解度的相互作用^[39,40]。温度升高为腐蚀反应提供足够的活化能，加速腐蚀反应，然而，温度的升高降低了H₂S及CO₂的溶解度。此外，温度还影响腐蚀产物的成膜机制，有可能抑制腐蚀。综合上述原因，管道腐蚀速率起初随着温度的升高而急剧增加，随后增势逐渐放缓，直至达到某一临界温度点(60~100 ℃)，在此之后腐蚀速率开始出现下降趋势^[41,42]。由图5中PGNN-IPSO的温度对腐蚀速率影响的PDP图可知在40 ℃前，预测得到的腐蚀速率随着温度的升高而明显上升，但超过40 ℃时增速显著放缓。相较于ANN-IPSO模型，PGNN-IPSO模型未显示出提前到达温度临界点的现象，这反映了加入机理引导后的模型在遵循腐蚀基本机制上的稳定性，避免了过度拟合数据噪声。不过，由于数据的分布不均和噪声干扰，PGNN-IPSO模型在描述高温区域的腐蚀规律时仍然不够理想。

在H₂S占比较低时，少量水相H₂S吸附在钢表面，干扰了电化学反应，使腐蚀速率增幅不明显^[20]。然而，随着H₂S占比增加，其对腐蚀总体还原作用的贡献超过了前述影响，促使Fe快速溶解，进而增加腐蚀速率^[43]。但当H₂S占比过高时，将形成保护性的硫化铁腐蚀产物层，使腐蚀速率上升趋势逐渐放缓^[42,44]。PGNN-IPSO模型也成功捕捉到这一规律。

一般认为较高流速会使腐蚀性介质扩散并破坏产物膜，进一步加剧腐蚀，因此腐蚀速率随流速增加而增大。图5中展示的腐蚀速率随流速变化的规律也符合该趋势。

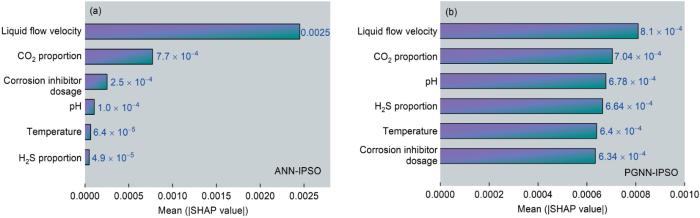
Nesic等^[37]的研究表明，当pH低于4时，H⁺还原反应占主导地位，而pH大于5时，主要反应为碳酸的还原反应。在这个反应机制过渡期间，腐蚀速率发生较大变化，过渡完成后，pH对腐蚀速率的影响趋于平缓^[20,45]。PGNN-IPSO模型很好地诠释了这一规律。

缓蚀剂注入量可以在几乎不存在起始阈值的情况下快速降低管道的腐蚀速率。低浓度的缓蚀剂虽无法产生均匀致密的保护膜，但仍在一定程度上起到缓蚀作用。随着缓蚀剂浓度提高，钢铁表面的缓蚀剂吸附量逐渐达到饱和，同时由于缓蚀剂分子间的位阻效应，使腐蚀速率下降幅度逐渐减小^[44,46]。这也与PGNN-IPSO模型学习到的规律一致。

为了更全面地了解各个特征对预测结果的影响，本研究进行了SHAP研究。SHAP被用于量化特征对模型输出的影响，平均绝对SHAP值也用于描述特征的重要性，但需注意的是，该特征重要性仅相对于本数据集的数据分布而言。如图6所示，在ANN-IPSO及PGNN-IPSO中，液体流速展现出最高的重要性，平均绝对SHAP值分别为0.0025和0.00081。这表明，平均而言，液体流速使数据集中所有样本的腐蚀速率预测值增加或减小了0.0025和0.00081。差异较大的原因是在ANN-IPSO中，预测结果对其他特征的依赖过小，可能是该模型学习到了错误规律导致过拟合的结果。相比之下，PGNN-IPSO模型的预测结果对各特征的依赖更加平衡，各特征的平均绝对SHAP值相近，说明各特征对预测结果都产生了较大的影响。然而，平均绝对SHAP值不能区分特征对腐蚀速率影响的方向。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 特征的平均绝对SHAP值

Fig.6 Mean SHAP value of features: (a) ANN-IPSO, (b) PGNN-IPSO

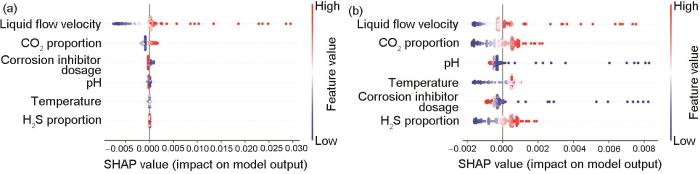
因此，图7展示了所有样本中各特征的SHAP值的全局分布，负SHAP值表示特征对预测有负面影响，导致预测结果减小。相反，正的SHAP值表示正面的影响，导致更高的预测结果。这些特征已被缩放到相同的范围，颜色表示这些特征的值，蓝色和红色分别表示低和高的特征值。图案的宽度表示数据的集中程度。可以观察到，液体流速、CO₂占比、H₂S占比和温度越高，腐蚀速率越高。相比之下，较高水平的pH和缓蚀剂注入量显示出负的SHAP值，表明高pH和高缓蚀剂注入量能有效降低管道腐蚀速率，与腐蚀机理相符。而未引入腐蚀机理的ANN-IPSO模型对各特征的影响混乱，与腐蚀机理相悖。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 SHAP值摘要图

Fig.7 SHAP value summary plot: (a) ANN-IPSO, (b) PGNN-IPSO

4 结论与展望

本研究利用PGNN-IPSO模型和可解释性方法对管道腐蚀进行预测和分析。验证了改进模型的表现，并通过可解释性方法深入探究了预测逻辑，结合腐蚀机理进行了定量分析。得出以下结论：

(1) 相较于ANN模型，本研究建立的PGNN模型在预测腐蚀行为方面表现出更佳的性能。在相同的超参数优化算法(PSO)下，预测结果的MAPE降低了0.47%。

(2) 与PSO算法相比，本研究采用的IPSO优化算法表现出更强的寻优性能。在相同的预测模型(ANN)下，预测结果的MAPE降低了0.06%。

(3) 通过可解释性方法，分析了各腐蚀特征对腐蚀速率的影响，并与腐蚀机理相互映照。PGNN-IPSO模型捕捉到了正确的腐蚀规律，腐蚀特征对腐蚀速率的影响与腐蚀机理一致。而ANN-IPSO虽然在数据集上表现准确，但实际上学到了与腐蚀机理相悖的错误规律，外泛化能力不足。因此，在小规模数据集情况下，仅凭验证集上的准确度来评估模型性能的方法存在缺陷，应结合可解释性方法和先验知识进行分析。

本研究展示了物理引导神经网络预测模型在预测集输管道内腐蚀速率时的良好性能，特别是在其预测逻辑与腐蚀机理的契合程度方面。鉴于此模型能够深度融合先验物理知识与数据驱动的学习能力，其在未来科学研究与工程应用中的潜力较大，尤其是在那些物理现象复杂、难以直接准确建模的领域，如腐蚀科学、生物医学信号分析、能源系统优化等。然而，进一步优化物理规律与数据驱动学习的协同训练策略，以及定量评估物理引导对模型精度、鲁棒性与外泛化能力的提升效果，仍是该领域亟待解决的关键问题。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Wang

Q Y

, Song

Y H

, Zhang

X S

, et al.

Evolution of corrosion prediction models for oil and gas pipelines: from empirical-driven to data-driven

[J]. Eng. Fail. Anal., 2023, 146: 107097

[本文引用: 2]

[2]

Wang

B Q

, Mu

Y Q

, Shen

F M

, et al.

Identification of corrosion factors in blast furnace gas pipe network with corrosion big data online monitoring technology

[J]. Corros. Sci., 2024, 230: 111906