我国不同地区钢材大气腐蚀预测算法评估与筛选

doi:10.11902/1005.4537.2023.257

我国不同地区钢材大气腐蚀预测算法评估与筛选

沈坚¹^,², 吴柯娴^,¹^,²^,³, 何晓宇¹^,², 方兴龙⁴

1.浙江数智交院科技股份有限公司杭州 310006

2.综合交通运输理论交通运输行业重点实验室杭州 310006

3.浙江大学结构工程研究所杭州 310058

4.浙江海港内河港口发展有限公司杭州 310005

Evaluation and Screening of Atmospheric Corrosion Prediction Algorithms of Steels in Different Regions of China

SHEN Jian¹^,², WU Kexian^,¹^,²^,³, HE Xiaoyu¹^,², FANG Xinglong⁴

1. Zhejiang Institute of Communications Co., Ltd., Hangzhou 310006, China

2. Key Laboratory of Integrated Transportation Theory and Transportation Industry, Hangzhou 310006, China

3. Institute of Structural Engineering, Zhejiang University, Hangzhou 310058, China

4. Zhejiang Seaport River Port Development Co., Ltd., Hangzhou 310005, China

通讯作者: 吴柯娴，E-mail:wukexianzju@163.com，研究方向为结构性能评估、全寿命设计及优化

收稿日期: 2023-08-17 修回日期: 2023-10-23

基金资助:

浙江省交通运输厅科技计划项目.  2020003
浙江省交通运输厅科技计划项目.  2023007
交通运输行业重点科技项目.  2020-GT-010

Corresponding authors: WU Kexian, E-mail:wukexianzju@163.com

Received: 2023-08-17 Revised: 2023-10-23

Fund supported:

Science and Technology Plan Project of Zhejiang Provincial Department of Transportation.  2020003
Science and Technology Plan Project of Zhejiang Provincial Department of Transportation.  2023007
Transportation Industry Key Technology Project.  2020-GT-010

作者简介 About authors

沈坚，男，1969年生，正高级工程师

摘要

针对我国不同地区的各类钢材，提出了一种基于机器学习算法的钢材大气腐蚀深度预测方法，并对不同算法的适用程度进行评估。首先，收集了我国10个大气暴露站的腐蚀检测数据、环境特征和材料特征，采用规范公式与6种机器学习算法预测钢材腐蚀深度，分析预测误差，对比环境腐蚀性等级评估的准确率，筛选适用于我国钢材大气腐蚀的预测模型。进一步分析材料与环境特征敏感性，揭示影响钢材大气腐蚀的主要材料与环境因素。结果表明，相比于规范公式，应用随机森林(RF)和长短期记忆循环神经网络(LSTM)算法的预测模型精度大幅提升；除了规范公式中的温湿度、硫酸盐和氯盐沉积率外，有关雨水酸碱性和雨水腐蚀性离子浓度的特征对钢材腐蚀行为有较大影响，应予以考虑。

关键词： 钢材 ; 大气暴露站 ; 机器学习 ; 特征敏感性 ; 环境腐蚀性等级

Abstract

Atmospheric corrosion of steels is a universal problem. Improving the prediction accuracy of atmospheric corrosion rate of steels in China is of great significance for setting corrosion margin, preventing corrosion failure and reducing the corrosion induced economic loss. For different type of steels in different regions of China, a prediction method of corrosion depth for steels based on machine learning algorithm was proposed, including data acquisition and processing, model training and testing, model evaluation and screening, feature ranking and other steps. The applicability of different algorithms was evaluated and the optimal algorithm of the corrosion prediction for steels was selected. Firstly, the corrosion data, environmental- and materials-features of 10 atmospheric exposure stations in China were collected. The corrosion depth of steels was predicted by using standard formulas and 6 machine learning algorithms. The grades of environmental corrosivity of atmospheric exposure stations were evaluated. Then, the prediction errors were analyzed, the accuracy of environmental corrosivity grade assessment was compared, and the prediction model suitable for steel corrosion was screened. Moreover, the sensitivity of materials- and environmental-features were analyzed, revealing the main factors of environments and materials affecting the atmospheric corrosion of steels. The results show that compared with the standard formula, the accuracy of the prediction models is greatly improved by RF and LSTM algorithms. In addition to the terms such as temperature, humidity, sulfate- and chloride-deposition rates mentioned in standard formulas, the acidity, alkalinity and rainwater corrosive ion concentration of rainwaters have a great impact on the corrosion of steels, which should be considered.

Keywords： steel ; atmospheric exposure stations ; machine learning ; feature sensitivity ; environmental corrosive grade

PDF (2940KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

沈坚, 吴柯娴, 何晓宇, 方兴龙. 我国不同地区钢材大气腐蚀预测算法评估与筛选. 中国腐蚀与防护学报[J], 2024, 44(4): 939-948 DOI:10.11902/1005.4537.2023.257

SHEN Jian, WU Kexian, HE Xiaoyu, FANG Xinglong. Evaluation and Screening of Atmospheric Corrosion Prediction Algorithms of Steels in Different Regions of China. Journal of Chinese Society for Corrosion and Protection[J], 2024, 44(4): 939-948 DOI:10.11902/1005.4537.2023.257

钢材大气腐蚀是指暴露在大气中的钢材表面与周围环境发生化学、电化学或物理作用，从而造成材料失厚或失重，性能下降乃至失效的过程，其普遍存在于制造业、建筑业、交通运输业等领域^[1]。准确认识并预测钢材的腐蚀行为和失厚速率对于设定腐蚀裕量、预防腐蚀失效、降低腐蚀成本具有重要意义。以往研究多采用室内加速实验或室外暴露实验数据开展钢材腐蚀研究，重点分析钢材大气腐蚀的环境因素、材料因素和时间因素^[2]。为了进一步获得具有地方腐蚀特性的长期室外暴露腐蚀数据，中国科技部国家材料环境腐蚀野外科学观测研究平台^[3]自1984年在全国多个具有典型气候特征的地方建立大气腐蚀站点，并在每个站点开展了多种金属材料的大气挂片实验，目前已经积累了大量的腐蚀数据。

近年来，随着人工智能的兴起，机器学习、深度学习等技术为处理高维数据、挖掘特征关系、精准预测腐蚀速率提供了新的思路^[4~6]。支元杰^[7]以17种低合金钢在6个大气站共409项大气腐蚀数据为样本，采用线性回归、人工神经网络(ANN)、随机森林(RF)、支持向量机(SVM)和基于加权Ｋ近邻的随机森林动态集成选择算法(RF-WKNNs)进行分析，给出了大气环境特征对腐蚀速率影响的定量分析，进一步提出全连接级联动集成选择森林算法(DCCF-WKNNs)并预测腐蚀失厚率。结果表明，改进后的模型对于大气环境下的小样本低合金钢腐蚀数据预测具有较高准确性和泛化性，重要性较高的环境特征为雨水pH、SO₂浓度、Cl⁻浓度、年平均相对湿度(RH)、年平均温度(T)和降雨量(P_rain)。其另一篇论文^[8]对Q235钢的大气腐蚀数据分析表明贡献度较高的环境特征还包括NO₂和自然降尘量(水溶性和非水溶性)。

除了长周期的大气腐蚀数据外，一些学者采用腐蚀监测仪获取了大量短周期大气腐蚀数据。杨小佳^[9]采用大气腐蚀传感器获取了含Cr低合金钢在琼海站12个月的环境特征和腐蚀电流，通过ANN、RF、SVM和深度神经网络模型挖掘环境、材料成分及结构特征对低合金钢耐蚀性的影响。结果表明，含Cr低合金钢腐蚀的主要环境特征为RH、T、P_rain、CO和SO₂等，材料成分特征中Cr的影响大于Mo和Sn，微观组织结构中的M-A组元比例、晶粒平均取向差等也对腐蚀速率有较大影响。Li等^[10]收集了碳钢在青岛站12个月的环境特征和腐蚀电量，通过RF预测表明锈层、风速、P_rain、RH和Cl⁻浓度对碳钢腐蚀有较大的影响，且风速在腐蚀初期的影响最大。Pei等^[11]进一步明确了RF模型在预测瞬时大气腐蚀方面表现出比ANN和SVM更高的精度。张明等^[12]收集了45号钢在5个大气站1个月的环境特征和腐蚀电流，基于RF、BP神经网络(BPNN)和梯度提升回归树(GBRT)的多模型集成重要变量选择算法(MEIVS)，量化不同地区钢材早期大气腐蚀过程中环境变量的重要性，结果表明重要的环境特征为RH、P_rain、T和臭氧浓度等。

大气腐蚀监测仪获得的数据量大，可达到百万级，但实验周期短，现有数据集主要是针对某个或某几个大气站的短期数据，无法反映长期腐蚀趋势，无法确定腐蚀预测模型对其他地区、其他型号钢材的适应度。大气站传统腐蚀检测方法所得数据的实验周期跨度大，目前最长腐蚀周期为16年，实验数据能够真实反映不同地区、不同时期、不同型号钢材的腐蚀速率。但以往研究中采用的大气站腐蚀检测数据量较小，考虑的环境和材料特征相对较少，未采集具有特殊气候大气站的腐蚀数据(如万宁、拉萨等)。此外，对于深度学习算法，如循环神经网络(RNN)、卷积神经网络(CNN)的应用尚未开展。

针对以上不足，本文收集了我国10个大气站的腐蚀检测数据、环境特征以及材料组成特征，采用6种机器学习算法对我国大气站环境腐蚀性等级与钢材腐蚀速率进行评估与预测，分析我国规范公式与各类机器学习算法对腐蚀深度预测的误差，明确泛化性更强、准确度更高的腐蚀深度预测模型，揭示影响腐蚀的主要环境与材料组成特征。

1 数据采集与处理

机器学习的核心在于数据支持与驱动，必须收集到充足的、能够覆盖大部分应用场景的数据集，才可能训练出精度较高、泛化能力较强的模型^[13]。本节描述了腐蚀数据集和环境数据的采集和处理过程，进一步基于时间、材料、环境特征与腐蚀深度的相关性进行特征降维，为模型训练提供数据集。

1.1 数据采集

采集我国10个大气站1984~2016年的腐蚀数据与环境特征，数据来源为中国腐蚀与防护网数据管理系统^[14]。其中，10个大气站分别为万宁(WN)、江津(JJ)、青岛(QD)、琼海(QH)、广州(GZ)、北京(BJ)、武汉(WH)、沈阳(SY)、敦煌(DH)和拉萨(LS)。

腐蚀数据共1364组，每组包括钢材牌号、钢材类别、实验地点、实验开始时间、实验结束时间、实验周期t/month和腐蚀失厚率r_corr / (μm·a^-1)。钢材牌号共34种，可分为9类，分别为碳素结构钢(273组)、优质碳素结构钢(103组)、低合金钢(411组)、不锈钢(107组)、耐候钢(348组)、普通冷轧钢(37组)、细晶粒结构钢(37组)、弹簧钢(27组)和稀土结构钢(21组)。其中，低合金钢、耐候钢、碳素结构钢约占总体数据量的76%。经统计，10个大气站的腐蚀数据箱型图见图1。可以看出，腐蚀失厚率变化幅度较大，万宁站、青岛站、琼海站和沈阳站离群值较多。其中，万宁站和沈阳站腐蚀失厚率的变异系数达到0.95以上，不确定性较高。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 大气站腐蚀数据箱型图

Fig.1 Box plot of atmospheric station corrosion data

环境数据共21768个，包括实验地点、实验时间、海拔H/m、温度T/℃、湿度RH/%、降水量P_rain/_{mm、海盐粒子沉积率D_seasalt/_{10^-2 mg·cm^-2·d^-1、硫酸盐化速率D_sulfation/_{10^-2 mg·cm^-2·d^-1、NH₃沉积率D $_{N H_{3}}$ /_{10^-2 mg·cm^-2·d^-1、NO₂沉积率D $_{N O_{2}}$ /_{10^-2 mg·cm^-2·d^-1、H₂S沉积率D $_{H_{2} S}$ /_{10^-2 mg·cm^-2·d^-1、雨水pH值R_pH、雨水SO $_{4}^{2 -}$ 浓度R $_{S O_{4}^{2 -}}$ _{/_{mg·m^-3、雨水Cl^-浓度R_Cl⁻/_{mg·m^-3、自然降尘量D_dust/_{g·cm^-2·month^-1、日照时数t_sun/_{h和平均风速V_wind/_m·s^-1。}}}}}}}}}}}

1.2 数据处理

处理腐蚀数据和环境数据，得到可用于机器学习算法的数据集。首先，提取腐蚀数据中的钢材牌号，使用化学元素含量来表示各牌号钢材之间的差异，化学成分包括：Fe、C、P、S、Si、Ni、Cr、Cu、Mn、Mo、Al、V、Ti和Nb。其次，提取腐蚀数据的实验开始时间和结束时间，在环境数据中寻找对应时间范围的15项环境数据，按月平均值统计。计算该时间范围内环境数据月平均值的指数移动平均值(β = 0.9)作为环境参数输入量。另外，将腐蚀失厚率乘以实验周期得到腐蚀深度D_corr/μm作为输出量进行训练和测试。进一步计算皮尔逊相关系数矩阵以明确输入量与输出量的相关关系，其中，时间特征(实验周期)与输出量的相关系数为0.36，材料特征、环境特征与输出量的相关系数矩阵热力图见图2。可以看出，Fe与Cr、Ni相关系数较高，可达0.97，降水量与温度、湿度相关系数较高，可达0.93。为了提高输入量的质量，应剔除数据集中相关性过高的特征，因此删除Fe含量与降水量这两项输入特征。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 腐蚀深度与特征的相关系数矩阵热力图

Fig.2 Heat maps of corrosion depth and characteristic correlation coefficient matrix: (a) material features, (b) environment features

经过上述处理，可构建一个包含1364条腐蚀样本的数据集，每个样本包含1项时间特征(实验周期)、13项材料特征(化学成分含量)、14项环境特征，共计28维特征作为输入量，1项腐蚀深度作为输出量。

2 预测模型与方法

传统钢材腐蚀深度预测模型一般采用幂函数^[15]形式。而机器学习算法则直接挖掘样本输入量与输出量之间的映射关系，计算精度更高。本节介绍规范公式，给出公式参数取值，并介绍机器学习算法架构，明确超参数设定，为钢材大气腐蚀深度预测提供具体模型。

2.1 规范公式

依据《金属和合金的腐蚀大气腐蚀性第1部分：分类、测定和评估》(GB/T 19292.1-2018)^[16]中的规定，碳钢腐蚀深度与暴露时间、化学成分含量、环境参数等12维数据有关。碳钢大气腐蚀深度D_corr为

D_{c o r r} = r_{c o r r, 1} \cdot t^{(0.569 + \sum b_{i} w_{i} + 0.0845 S_{d}^{0.26})}

(1)

r_{c o r r, 1} = 1.77 \cdot P_{d}^{0.52} \cdot e x p (0.020 \cdot R H + f_{s t}) +

0.102 \cdot S_{d}^{0.62} \cdot e x p (0.033 \cdot R H + 0.040 \cdot T)

(2)

式中：D_corr为碳钢腐蚀深度，μm；t为暴晒时间，a；r_corr,1为第一年腐蚀速率，μm/a；T为年平均温度，℃；RH为年平均湿度，%；P_d为年平均SO₂沉积率，mg·m^-2·d^-1；S_d为年平均Cl^-沉积率，mg·m^-2·d^-1；w_i 为第i个化学元素的质量百分比；b_i 为第i个化学元素的影响系数^[17]，见表1； f_st为碳钢相关系数，可采用下式计算：

f_{s t} = \{\begin{matrix} 0.150 \cdot (T - 10) & T \leq 10^{o} C \\ - 0.054 \cdot (T - 10) & T > 10^{o} C \end{matrix}

(3)

表1 化学元素的影响系数

Table 1 Influence coefficients of chemical elements

Chemical element	b_i
C	-0.084
P	-0.490
S	+1.440
Si	-0.163
Ni	-0.066
Cr	-0.124
Cu	-0.069

新窗口打开| 下载CSV

根据GB/T 19292.2-2018^[17]规定，暴露20 a之后的腐蚀速率是线性的，总腐蚀深度为

D_{c o r r} (t > 20) = r_{c o r r, 1} \cdot [20^{b} + b (20^{b - 1}) \cdot (t - 20)]

(4)

式中，b为碳钢环境特性参数。

2.2 机器学习算法

本文涉及的机器学习算法为有监督学习算法(回归)，包括SVM、RF、径向基函数神经网络(RBFNN)、BPNN、长短期记忆循环神经网络(LSTM)和CNN。基本建模步骤如下：首先，划分训练集与测试集。打乱数据集，将数据划分为用于训练算法模型的训练集和用于评估模型性能的测试集，划分比例取70%和30%。将测试集和训练集数据归一化到区间[0, 1]，避免数据的尺度效应。由于万宁站腐蚀失厚率高，远大于其他大气站，因此将万宁站与其他大气站数据集分开训练。其次，训练模型。选择对应的机器学习算法，分别确定万宁站和其他大气站数据的最优超参数。采用训练集训练机器学习算法模型，得到训练集的预测值。接下来，测试模型。采用测试集仿真测试，反归一化后得到测试集的预测值。计算预测值的误差评价指标，即决定系数(R²)、均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对误差率(MAPE)。最后，分析敏感性。采用平均影响值(MIV)法评估各类模型特征的敏感性。将归一化后的特征数值增大20%，输入训练好的模型中计算预测值。同时，将归一化后的特征数值减小20%计算得到预测值，两组预测值之差的平均值即为MIV。将MIV除以原预测值得到平均相对影响值，进一步计算得到28维特征的平均相对影响值百分比，确定敏感性较大的特征。另外，依据GB/T 19292.1-2018^[16]评估大气环境的腐蚀性等级，与实际等级对比，分析不同模型的准确性大小以及误差来源。

接下来分别介绍这6类算法的原理和超参数设定：

(1) SVM^[18]是用于分类和回归问题的有监督学习模型，其回归原理是将训练样本映射到高维特征空间，并在该空间中找到一个回归超平面使所有样本到该平面的距离最近。映射过程可采用不同的核函数。本文选取径向基函数核映射样本数据，采用matlab中的svmtrain函数训练模型，径向基函数参数取0.8。训练万宁站数据时惩罚因子取1.2；训练其他大气站数据时惩罚因子取3。

(2) RF^[19]是一种用于分类、回归和其他任务的集成学习方法，其回归原理是通过随机抽取样本和特征，构建大量互不关联的决策树来训练模型，最终返回各个树的平均值。采用matlab中的TreeBagger函数训练模型，损失函数为MSE，决策树数目取500，最小叶子数取1，训练时计算特征的重要性。

(3) RBFNN^[20]是使用径向基函数作为激活函数的人工神经网络，RBFNN有3层，第1层为输入层，第2层为隐藏层，第3层为输出层。采用matlab中的newrbe函数构建网络并训练模型。训练万宁站数据时径向基函数的扩展速度取1200；训练其他大气站数据时径向基函数的扩展速度取300。

(4) BPNN是一种按误差反向传播算法训练的多层前馈网络^[21]，一般的3层BPNN包含输入层、隐藏层和输出层，每个神经元的输出由其输入之和的某种非线性函数计算。采用matlab中的train函数构建3层神经网络并训练模型，损失函数为MSE，迭代次数为1000，误差阈值为10^-6，学习率为0.01。训练万宁站数据时隐藏神经元个数取5；训练其他大气站数据时隐藏神经元个数取10。

(5) LSTM^[22]是一种适用于基于时间序列的数据分类、处理和预测RNN，可处理传统RNN中存在的梯度消失问题，在长序列训练中有更好的表现。训练前将数据集按照实验周期升序排列，采用matlab中的trainNetwork函数构建LSTM网络并训练数据，网络包括序列输入层、LSTM隐藏神经元层、ReLU激活层、全连接层和回归输出层，损失函数为MSE，优化器采用自适应矩估计(Adam)，隐藏神经元为20个，批处理样本为300个，最大迭代次数1200，初始学习率为0.01，经过800次训练后学习率降低为0.005。

(6) CNN^[23]是一种常用于视觉图像分析的人工神经网络，使用卷积运算来代替一般矩阵乘法。由于CNN可用于处理时序问题，本文对CNN也进行考虑。采用matlab中的trainNetwork函数构建CNN网络并训练数据，网络包括图像输入层、卷积层(卷积核大小为3 × 1，生成16张特征图)、批量归一化、ReLU激活层、最大池化层、卷积层(卷积核大小为3 × 1，生成32张特征图)、批量归一化、ReLU激活层、最大池化层、全连接层和回归输出层，损失函数为MSE。训练时优化器采用自适应矩估计(Adam)，初始学习率为0.01。训练万宁站数据时批处理样本为3个，最大训练次数为150，经过120次训练后学习率降低为0.005；训练其他大气站数据时批处理样本为50个，最大训练次数为600，经过400次训练后学习率降低为0.005。

3 预测结果与分析

不同机器学习算法有不同的应用场景，需要根据实际情况选择合适的算法^[13]。本节采用GB/T 19292规范公式与6种机器学习算法对钢材大气腐蚀深度进行预测，通过误差分析对比规范公式与机器学习算法在该问题上的适用性，确定最优预测方法。此外，计算特征的重要性与敏感性，分析对钢材腐蚀影响较大的材料特征与环境特征。进一步通过腐蚀性环境等级预测的准确率评估最优预测方法对规范公式预测性能的提升程度。

3.1 误差分析

规范公式和6种机器学习算法对钢材大气腐蚀深度的预测结果见图3，其中，D_real与D_pred分别为腐蚀深度的真实值和预测值，GB是指采用我国GB/T 19292规范公式计算得到的结果。训练集和测试集的散点越接近于y = x直线，预测效果越好。可以看出，规范公式对腐蚀深度较大的样本预测结果并不理想，远小于真实值，尤其是腐蚀深度离群样本误差极大。而机器学习算法的预测效果展现出明显的优势，尤其以FR、LSTM、BPNN的预测效果更优。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同方法对腐蚀深度预测结果

Fig.3 Prediction results of corrosion depth by GB (a), SVM (b), RF (c), RBFNN (d), BPNN (e), LSTM (f) and CNN (g)

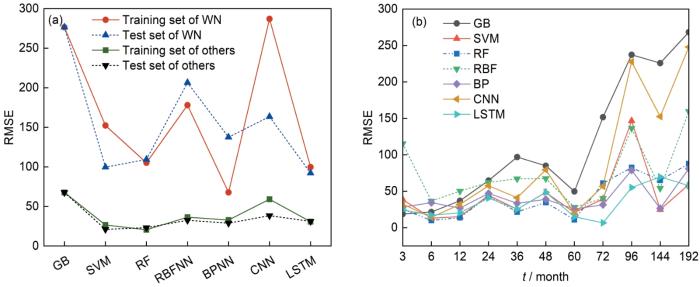
按照规范公式，万宁站数据预测误差指标R²为0.23，RMSE为276.50，MAE为127.56，MAPE为15.01；其他大气站数据预测误差指标R²为0.24，RMSE为67.65，MAE为43.14，MAPE为8.45。表2给出了应用不同机器学习算法对大气腐蚀深度预测结果的误差指标。图4a描述了规范公式与不同机器学习算法在不同地区数据集上的RMSE。通过对比可以看出，6种机器学习算法腐蚀深度预测结果的误差远小于规范公式的预测误差，可见采用数据驱动的机器学习算法可以提升腐蚀深度预测的准确性。但并非所有算法都适用于钢材腐蚀深度预测问题，CNN在万宁站数据集上的性能极差，并不适用于此类回归问题；RBFNN在万宁站数据集上的预测性能相对较差，误差远大于RF与LSTM的预测结果，因此应避免选择这两类算法进行腐蚀预测；BPNN与采用RBF核函数的SVM在训练万宁站数据集的过程中不确定性较高，输出结果与数据集的划分有关，模型鲁棒性较差；RF与LSTM在所有大气站数据集上预测结果的误差相对较低，模型具有较好的鲁棒性，其中，LSTM在万宁站数据集上的表现更好，能够准确预测极端值，而RF在其他大气站数据集上的表现更好，误差最低。

表2 不同机器学习模型预测结果的误差指标

Table 2 Error metrics of prediction outcomes for different machine learning models

Atmospheric station	Error indicator	Sample set	SVM	RF	RBFNN	BPNN	LSTM	CNN
WN	R²	Training set	0.81	0.91	0.70	0.95	0.91	0.33
	R²	Test set	0.74	0.65	0.48	0.85	0.87	0.38
	RMSE	Training set	152	105	178	68	100	287
	RMSE	Test set	100	109	206	137	92	163
	MAE	Training set	45	52	103	43	61	131
	MAE	Test set	59	69	140	75	58	94
	MAPE	Training set	265%	252%	521%	264%	254%	1511%
	MAPE	Test set	263%	272%	2220%	127%	1454%	304%
Others	R²	Training set	0.90	0.94	0.80	0.85	0.85	0.49
	R²	Test set	0.86	0.84	0.76	0.77	0.82	0.65
	RMSE	Training set	27	21	36	33	31	59
	RMSE	Test set	21	23	33	29	31	38
	MAE	Training set	10	7	20	19	15	28
	MAE	Test set	15	13	24	20	18	23
	MAPE	Training set	130%	29%	202%	215%	60%	569%
	MAPE	Test set	141%	57%	267%	156%	133%	237%

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 大气腐蚀深度预测结果的RMSE

Fig.4 RMSE of prediction results of atmospheric corrosion depth: (a) different regional datasets, (b) different experiment periods

图4b进一步描述了规范公式与不同机器学习算法在不同实验周期上的RMSE。整体上，RMSE随着实验周期的增长而逐步增大，规范公式在腐蚀初期(3~24个月)的预测精度较高，而在之后误差快速增长，预测精度小于机器学习算法的精度。当实验周期在60个月以内时，RF的预测效果更好，而当实验周期在60个月以上时，LSTM的预测效果更好。综合考虑以上内容，针对钢材大气腐蚀深度预测这一回归问题，推荐选择RF或LSTM进行模型训练与预测，对于需要考虑较多离群样本的长时间序列问题，采用LSTM更优。

3.2 敏感性分析

采用MIV法计算规范公式和机器学习算法对28维特征的平均相对影响值百分比，结果见表3。可以看出，不同预测方法的敏感性分析结果存在较大差异。若依据规范公式计算得到的敏感性排序，则前3项重要材料特征为：S>Si>P，前3项重要环境特征为：平均相对湿度>硫酸盐化速率>海盐粒子。若依据RF计算得到的敏感性排序，则前3项重要材料特征为：Si>C>P，前3项重要环境特征为：雨水pH>日照时数>海盐粒子。若依据LSTM计算得到的敏感性排序，则前3项重要材料特征为：Cr>Si>P，前3项重要环境特征为：雨水pH>平均相对湿度>平均温度。

表3 不同机器学习模型的特征敏感性指标

Table 3 Feature sensitivity metrics for different machine learning models

Features	GB	SVM	RF	RBFNN	BPNN	LSTM	CNN	RF importance
Experiment time	16.1%	6.8%	18.1%	5.5%	7.4%	17.6%	31.2%	15.0%
R_pH	-	18.1%	27.8%	22.2%	52.1%	14.5%	0.1%	9.6%
Cr	0.1%	6.5%	0.3%	2.5%	3.2%	8.1%	4.5%	8.1%
R $_{S O_{4}^{2 -}}$	-	3.9%	1.4%	5.5%	1.4%	1.5%	20.1%	5.6%
t_sun	-	2.7%	5.5%	3.2%	3.9%	0.5%	0.5%	5.5%
D_dust	-	1.5%	2.4%	0.5%	0.6%	1.8%	1.0%	5.2%
D_sulfation	10.3%	3.1%	0.1%	2.1%	0.4%	2.0%	0.2%	4.6%
T	4.7%	3.3%	2.5%	3.8%	3.9%	4.2%	9.8%	4.5%
D $_{N O_{2}}$	-	2.2%	0.9%	3.1%	0.5%	3.0%	0%	4.4%
C	0%	5.6%	6.7%	1.5%	0.5%	1.1%	0.1%	4.3%
Cu	0.1%	3.0%	0.6%	10.7%	1.9%	2.6%	0%	3.9%
Si	0.5%	1.0%	7.9%	4.5%	1.9%	5.5%	0.4%	3.3%
D_seasalt	7.1%	0.1%	4.9%	1.5%	2.0%	3.8%	0.1%	3.2%
D $_{N H_{3}}$	-	1.5%	1.2%	2.3%	2.9%	1.0%	0%	3.2%
RH	59.5%	13.8%	3.3%	6.5%	5.6%	13.6%	7.1%	2.9%
H	-	0.1%	0.5%	0.6%	0.4%	1.3%	13.2%	2.9%
Mn	-	2.5%	2.8%	6.7%	0.6%	1.4%	0.7%	2.7%
S	1.0%	0.6%	3.5%	6.9%	2.3%	2.3%	0%	2.3%
D $_{H_{2} S}$		1.3%	1.0%	0.8%	0.2%	2.5%	0%	2.3%
P	0.4%	7.1%	6.3%	1.5%	3.6%	5.4%	0%	2.1%
R_Cl⁻	-	0.6%	1.6%	4.7%	2.6%	2.5%	10.8%	1.7%
V_wind	-	1.3%	0.3%	1.6%	0.8%	1.8%	0%	1.7%
Ni	0.1%	2.8%	0%	0.1%	0%	0.1%	0.1%	1.5%
Mo	-	0.1%	0.2%	0.1%	1.1%	0.4%	0%	0.7%
Ti	-	5.5%	0%	0.2%	0.2%	0.1%	0%	0%
V	-	3.1%	0%	1.0%	0.1%	1.0%	0%	0%
Nb	-	1.2%	0%	0.2%	0%	0.6%	0%	0%
Al	-	0.8%	0.1%	0.2%	0.1%	0%	0%	0%

Note: The first 10 items in descending order of feature sensitivity or importance are bolded.

新窗口打开| 下载CSV

此外，还计算了RF重要性指标，若依据RF重要性指标排序，则前3项重要材料特征为：Cr>C>Cu，前3项重要环境特征为：雨水pH > 雨水SO $_{4}^{2 -}$ > 日照时数。综合各类机器学习算法排序，相对更重要的特征前10项分别为：雨水pH、实验周期、平均相对湿度、雨水SO $_{4}^{2 -}$ 、平均温度、Cr、P、Si、雨水Cl⁻、Cu。其中，有关雨水酸碱性和雨水腐蚀性离子浓度的指标未能被规范公式考虑。

将28维特征归类为时间、材料和环境3类特征，对每类特征平均相对影响值百分比求和得到图5。规范公式中材料特征的敏感性仅为2%，而机器学习算法大幅提升了材料特征的敏感性。观察RF、LSTM敏感性和RF重要性百分比，对钢材大气腐蚀深度影响的重要性排序为：环境特征>材料特征>时间特征。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同机器学习模型3类特征敏感性百分比

Fig.5 Sensitivity percentages of three types of features for different machine learning models

3.3 准确率分析

根据GB/T 19292.1-2018^[16]的规定，可采用钢材暴露第1 a的腐蚀深度评估大气环境的腐蚀性等级(C1~CX)。经统计，大气站数据集中实验周期为12个月的样本有364个，按照规范公式和机器学习模型预测的大气环境腐蚀性等级准确率见图6。按照规范公式评估的腐蚀性等级准确率仅为40.1%，而机器学习算法评估的腐蚀性等级准确率平均为59%。其中，RF模型评估的准确率远高于其他机器学习算法模型，可达81.3%。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 模型预测准确率雷达图

Fig.6 Radar chart of prediction accuracies for various models

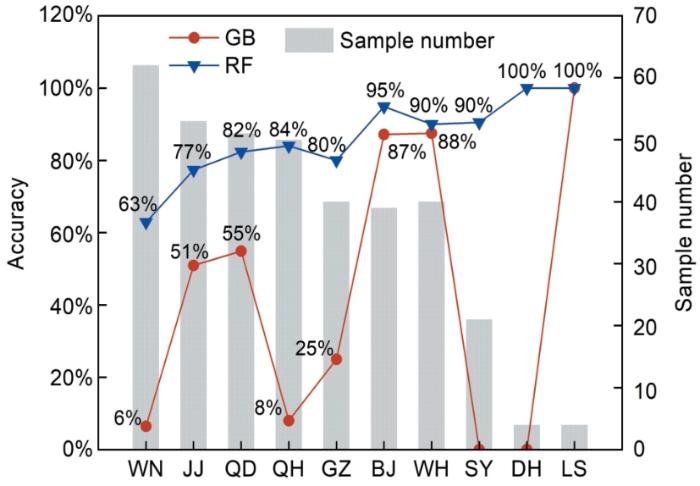
选择规范公式和RF模型评估误差来源进行详细分析，具体如图7和8所示。对于不同的钢材材料类型，按照规范公式评估的腐蚀性等级约有16.5%的评估等级小于实际等级，主要来源于对稀土结构钢、优质碳素结构钢、碳素结构钢的评估误差；约有43.4%的评估等级大于实际等级，主要来源于对不锈钢、弹簧钢和耐候钢的评估误差。而按照RF模型评估的腐蚀性等级约有4.7%的评估等级小于实际等级，主要来源于对普通冷轧钢和优质碳素结构钢的评估误差；约有14%的评估等级大于实际等级，主要来源于对弹簧钢和不锈钢的评估误差。对于不同的大气站，按照规范公式评估的腐蚀性等级在万宁站、琼海站、沈阳站和敦煌站的准确率极低，其中，98.54%的样本评估等级大于实际等级；在北京站、武汉站和拉萨站的准确率较高，误差主要来源于不锈钢。而不同大气站按照RF模型评估的腐蚀性等级准确率普遍高于规范公式，其中，万宁站评估的准确率略低，误差主要来源于耐候钢、不锈钢和低合金钢。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 大气环境腐蚀性等级评估准确率的材料类型差异

Fig.7 Differences in material types for assessing the accuracy of atmospheric corrosive grades: (a) GB, (b) RF

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 大气环境腐蚀性等级评估准确率的地区差异

Fig.8 Regional differences in the accuracy of atmospheric corrosive grade assessment

4 结论

(1) 针对钢材大气腐蚀深度预测问题，机器学习算法模型的预测精度高于规范公式，推荐选择RF或LSTM进行模型训练与预测。对于实验周期不超过60个月的预测问题，采用RF更优；而对于实验周期超过60个月或需要考虑极端值的长时间序列预测问题，采用LSTM更优。

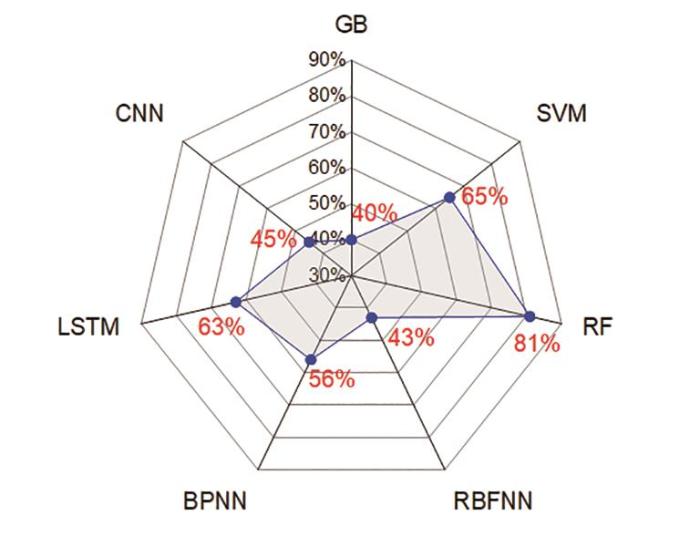
(2) 通过对所有预测模型的MIV分析和RF重要性分析，钢材大气腐蚀深度影响的特征排序为：环境特征>材料特征>时间特征。其中，重要的环境特征为：雨水pH、平均相对湿度、雨水SO $_{4}^{2 -}$ 浓度、平均温度和雨水Cl⁻浓度；重要的材料特征为：Cr、P、Si和Cu。有关雨水酸碱性和雨水腐蚀性离子浓度的指标尚未被现行规范考虑。

(3) 钢材暴露第1 a的腐蚀深度可作为大气环境腐蚀性等级的评估依据，按照规范公式评估的大气环境腐蚀性等级准确率仅为40.1%，而RF模型评估的准确率可达81.3%。对于不同钢材类型，不锈钢、弹簧钢和优质碳素结构钢的评估准确率较低；对于不同地区，万宁站的腐蚀样本数据不确定性较高，离群值多，评估准确率低。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Zhi

Y J

, Fu

D M

, Zhang

D W

, et al.

Prediction and knowledge mining of outdoor atmospheric corrosion rates of low alloy steels based on the random forests approach

[J]. Metals, 2019, 9(3): 383