纤维增强复合材料加固锈蚀箍筋混凝土梁的抗剪承载力计算模型分析

图1 试验梁尺寸及配筋示意图

Fig.1 Test beam size and reinforcement diagram (a) front elevation (b) cross section

表1 试验梁尺寸信息

Table 1 Size information of test beam

Beam	a_v / d	ƞ₀ / %	ƞ / %	Stirrup		FRP Stripe				V_u / kN
Beam	a_v / d	ƞ₀ / %	ƞ / %	R Area	UR Area	w_f / mm	t_f / mm	n	s_f / mm	V_u / kN
B1C	1	0	0	A6.5@120	B14@80	---	---	---	---	311.26
B1C5	1	5	4.86			---	---	---	---	313.56
B1C15	1	15	12.86			---	---	---	---	281.79
B1U	1	0	0			40	0.167	2	120	318.43
B1U5	1	5	5.62			40	0.167	2	120	321.67
B1U15	1	15	12.65			40	0.167	2	120	288.43
B2C	2	0	0			---	---	---	---	213.19
B2C5	2	5	5.56			---	---	---	---	212.28
B2C15	2	15	12.5			---	---	---	---	199.6
B2U	2	0	0			40	0.167	2	120	273.92
B2U5	2	5	4.81			40	0.167	2	120	280.63
B2U15	2	15	13.28			40	0.167	2	120	237.09
B3C	3	0	0			---	---	---	---	176.77
B3C5	3	5	4.96			---	---	---	---	177.01
B3C15	3	15	12.28			---	---	---	---	163.85
B3U	3	0	0			40	0.167	2	120	225.47
B3U5	3	5	5.08			40	0.167	2	120	230.71
B3U15	3	15	12.19			40	0.167	2	120	191.02

新窗口打开| 下载CSV

所采用的HPB300 (6.5 mm)、HPB335 (14 mm) 以及HRB400 (28 mm) 钢筋的屈服强度分别为200、475和410 MPa,弹性模量都为200 GPa。所采用的碳纤维增加复合材料(CFRP) 布厚度为0.167 mm,抗拉强度为3500 MPa,弹性模量为235 GPa。采用的建筑结构胶主要力学性能指标为抗拉强度55.5 MPa,拉伸弹性模量为3214.5 MPa,伸长率为2.2%。

所有试验梁的编号是根据剪跨比、箍筋锈蚀程度和加固方式来定的。B1、B2、B3分别表示剪跨比为1.0、2.0、3.0的试验梁；U表示U型加固梁,C表示未加固的控制梁；5、15分别表示箍筋设计锈蚀率为5%、15%。例如B1C,表示为剪跨比为1.0的控制梁 (箍筋没有发生锈蚀)；B2C5表示剪跨比为2.0、箍筋锈蚀率为5%的控制梁；B3U15表示剪跨比为3.0、箍筋锈蚀率为15%的U型加固梁。剪力荷载位移曲线如图2所示。

图2

图2 试验梁剪力-位移曲线

Fig.2 Shear-displacement curve of test beam

2 理论分析

2.1 箍筋屈服强度的折减

对于锈蚀钢筋,其屈服强度可用平均横截面积或最小横截面积计算。锈蚀钢筋通常在最小截面处发生破坏；因此,锈蚀钢筋的名义屈服强度因其非均匀分布而降低^[16,17]。正如公式 (1) 所示：

f_{y c} = (1 - η) f_{y v}

(1)

式中,f_yv和f_yc分别为锈蚀前后的箍筋屈服强度；η为实际的锈蚀率。而对于箍筋与混凝土之间的粘结暂不考虑,原因是试验证明箍筋锈蚀对箍筋与混凝土之间的界面影响较小,在锈蚀率较低的情况下,甚至能够提高粘结强度,从而提高梁的极限承载力,这与试验结果相符合。

2.2 梁截面面积的折减

钢箍锈蚀使梁截面发生混凝土保护层开裂、分层和剥落,在抵抗外部荷载时效果较差。El-Sayed等^[8]采用Higgins等^[9]提出的有效混凝土宽度模型。基于混凝土保护层厚度、箍筋直径和箍筋间距的模型表明：箍筋间距越近,腐蚀裂缝间的相互作用越强,且这种相互作用会导致剥落程度更加严重 (如图3所示),因此,混凝土梁的有效抗剪截面宽度表示为：

图3

图3 梁的横截面折减示意图

Fig.3 Diagram of beam cross-section reduction: (a) s<5.5c, (b) s=5.5c, (c) s>5.5c

b_{e f f} = b - 2 (c + d_{b}) s / 5.5 s < 5.5 c

(2)

b_{e f f} = b - 5.5 (c + d_{b})^{2} s / 5.5 s > 5.5 c

(3)

其中,b和b_eff分别为折减前后的梁横截面宽度,mm；c为梁的保护层厚度,mm；d_b为箍筋的直径,mm；s为箍筋的间距,mm。

Higgins等^[9]指出,公式 (2、 3) 适用于混凝土保护层失效的情况 (即一旦发现明显裂缝),一般来说,当锈蚀率大于10%的情况下,可以认为保护层已经全失效,这与文献^[2,10]的结果一致,从本文结果来看,也能看出这一规律,当箍筋锈蚀率大于10%时,抗剪承载力开始降低。值得注意的是,考虑到在锈蚀程度较大时,会对保护层进行凿除修复,但是钢筋依然会发生二次锈蚀,因此,在完成保护层的凿除修复后,对本公式的修正应该从锈蚀率为0开始重新定义锈蚀率大小,根据锈蚀率再次大于10%时才采用本公式进行计算。

2.3 FRP的抗剪承载力计算模型

如果FRP不受箍筋锈蚀的影响,则根据45°剪切裂缝穿过的FRP抗剪承载力公式计算：

ν_{f} = ϕ A_{f} E_{f} ε_{f} d_{f} / s_{f}

(4)

A_{f} = 2 n t_{f} w_{f}

(5)

其中,v_f为FRP抗剪贡献,kN； $ϕ$ 为FRP的加固折减系数,对于U型加固,取0.85,对于全包裹,取0.9；A_f为FRP条带的横截面积,mm²；E_f为FRP条带的弹性模量,GPa；ε_f为FRP条带的有效应变；d_f为FRP条带的有效高度,mm。

根据ACI 440.2R^[11]规范,FRP条带有效应变ε_f按照以下公式进行计算：

ε_{f} = k_{v} ε_{f u} \leq 0.004

(6)

k_{v} = k_{1} k_{2} L e / (11900 ε_{f u}) \leq 0.75

(7)

对于U型加固：

L_{e} = 23300 / (n t_{f} E_{f} 0.58)

(8)

k_{1} = (f_{c}^{'} {/ 27)}^{2 / 3}

(9)

k_{2} = (d_{f} - L_{e}) / d_{f}

(10)

对于全包裹：

ε_{f} = 0.004

(11)

其中,ε_fu为FRP的极限应变；k_v 为粘结折减系数；L_e为FRP条带的有效粘结强度,mm；k₁、k₂分别是混凝土强度和使用的加固类型的修正因子；f_c'为混凝土圆柱体抗压强度,kN。

2.4 SMCFT理论在FRP加固锈蚀箍筋混凝土梁的应用

SMCFT理论由Vecchio等^[12]和Bentz等^[13]提出的考虑未开裂混凝土中拉应力对RC构件的抗剪贡献的一种理论计算模型。其前身是修正压力场理论 (MCFT),MCFT理论假定主应力和主应变的方向一致,根据平衡条件、相容条件 (变形协调条件) 和物理条件 (混凝土和钢筋的应力-应变关系) 可以计算出RC构件在破坏时的斜裂缝倾角θ。SMCFT理论的主要的简化假设是无腹筋构件的抗剪强度是由骨料的咬合力控制的；同时还有另一个保守假设,即构件失效发生在箍筋屈服之前^[10]。通过限制应变,例如,箍筋屈服 (ε₂≥0.002)、混凝土压碎 (ε₂≈0.002) 以及将破坏时的纵向应变ε_x 限制在0.002,也可进一步简化。Bentz等^[13]研究表明,若RC构件在箍筋屈服前失效,可以假定此时RC梁的剪应力等于0.25f_c'；若RC梁失效时的剪应力低于这个值,可以推断出此时箍筋中的应力是等于其屈服强度的,即f_v =f_vy。简化修正压力场中的剪切力计算公式如下所示：

V为RC梁的抗剪承载力,其计算表达式为：

V = v b_{w} z

(12)

式中：v为RC梁横截面上的剪应力,Pa；b_w 为梁宽,mm；z为RC梁的内力臂高度,mm。

v = v_{c i} + ρ_{z} f_{y v} c o t θ v

(13)

v = f_{i} 1 c o t θ + ρ_{v} f_{y v} c o t θ

(14)

式中,ρ_v 为RC梁的配箍率,%。上述表达式 (13) 和 (14) 均可以写成：

v = β \sqrt[]{f_{c}^{'}} + ρ_{v} f_{y v} c o t θ

(15)

式中,v_c和v_s分别为混凝土和箍筋的抗剪贡献,kN；β为裂开混凝土中的拉应力系数,θ为平均裂缝角度。

那么此时计算RC梁的抗剪承载力的关键参数就剩下β和θ,Bentz等^[13]给出了它们的表达式为：

β = \frac{0.4}{1 + 1500 ε_{x}} \times \frac{1300}{1000 + s_{x e}}

(16)

θ = (29 + 7000 ε_{x}) (0.88 + \frac{s_{x e}}{2500}) \leq 75^{\circ}

(17)

式中,ε_x为纵向应变；s_xe为有效裂缝间距,mm。

在以上基础上,使用SMCFT理论计算RC梁抗剪承载力的步骤大致分为6步：即：(1) 估计纵向应变ε_x；(2) 计算有效裂缝间距s_xe；(3) 计算裂开混凝土中的拉应力系数β和平均裂缝角度θ；(4) 计算剪应力v；(5) 计算RC梁的抗剪承载力V；(6) 计算纵向应变ε_x',并根据所得结果返回去调整第 (1) 步的估计值,直至这两个结果收敛为止。

2.5 基于SMCFT理论的FRP加固锈蚀钢筋混凝土梁的计算模型

考虑箍筋锈蚀造成的箍筋屈服强度折减及混凝土梁保护层折减等因素。计算FRP加固锈蚀箍筋混凝土梁的计算模型及计算步骤如下所示：

(1) 给出纵向应变ε_x的一个估计值。

(2) 计算有效裂缝间距s_xe。

s_{x e} = \frac{35 s_{x}}{a_{g} + 16}

(18)

式中,s_x为纵向钢筋的垂直间距,mm；a_g为混凝土中的最大骨料粒径,mm。如果RC梁中的箍筋配置量超过规定的最小值,ρ_vf_yv>0.06 $\sqrt[]{f_{c}^{'}}$ ,则可视为裂缝的间距得到很好的控制,有效裂缝间距可保守地取值为s_xe=300 mm。若ρ_vf_yv<0.06 $\sqrt[]{f_{c}^{'}}$ ,有效裂缝间距s_xe按表达式 (18) 计算。

(3) 根据式 (16) 和 (17) 分别计算裂开混凝土中的拉应力系数β和平均裂缝角度θ。

(4) 根据式 (2) 和 (3) 计算有效截面宽度b_eff。

(5) 根据式 (19) 计算剪应力v_u。

\begin{array}{l} v_{u} = v_{c} + v_{s} + v_{f} = β \sqrt[]{f_{c}^{'}} + (1 - η) ρ_{v} f_{y v} c o t θ + \\ ρ_{f} f_{f} c o t θ \end{array}

(19)

其中,v_c和v_s分别为混凝土和箍筋的抗剪贡献,kN；f_f的计算需要考虑不同的加固方式,在全包裹加固时可直接采用有限应变ε_f=0.004时的有效应力进行计算；当U型加固时在达到其抗剪承载力时常发生以FRP剥离为主的破坏模式,此时FRP因达到与混凝土之间的最大粘结强度而剥离,因此,应该采用式 (6~ 10) 时的有效应变进行有效应力的计算。

(6) 根据式 (12) 计算RC梁的抗剪承载力V_u。

(7) 用式 (20) 计算纵向应变ε_x',并根据所得结果返回去调整第 (1) 步的估计值,直至这两个结果收敛为止。

ε_{x} = v \frac{1 + \frac{M}{V z}}{2 E_{s} ρ_{x}} = \frac{V + \frac{M}{z}}{2 E_{s} A_{s}}

(20)

式中,将纵向应变ε_x保守地取为RC梁底部纵筋受弯矩M和剪力V作用而产生的拉应变的一半；M为荷载在剪跨中部产生的弯矩,N·m,M=V·0.5a；ρ_x为纵筋的配筋率；E_s为纵筋的弹性模量,GPa；A_s为纵筋总的截面面积,mm²。

具体的计算步骤按照流程图4所示。

图4

图4 模型计算流程图

Fig.4 Flow chart of model

3 数据分析及讨论

3.1 现有FRP加固锈蚀箍筋混凝土梁抗剪理论模型

表2所示为现有文献中的FRP加固锈蚀箍筋混凝土梁的抗剪承载力计算模型。其中,a_cv为混凝土抗剪能力系数 (一般受弯构件)；f_t为混凝土抗拉强度,kN； $ϕ$ 为腐蚀对箍筋剪切能力贡献影响因子；A_v为箍筋截面面积,mm²；ρ_w为纵向受拉钢筋比,%；C_r为箍筋面积减少百分比,%；λ为影响混凝土密度的因子；A_w,eff为箍筋的有效面积,mm²；A_f,eff为FRP的有效截面积,mm²。

表2 现有文献中的计算模型汇总

Table 2 Summary of models in the existing literature

Model	V_c	V_s	V_f
Li et al^[14]	$a_{c v} f_{t} b h_{0}$	$ϕ f_{y v} A_{v} h_{0} / s$	$\frac{ϕ_{f} A_{f} E_{f} {ε_{f}}_{e} d_{f}}{s_{f}}$
EI-Maaddawy^[15]	2.2 ${(\frac{f_{c} ρ_{w} d}{a})}^{\frac{1}{3}} b_{w} d$	$(1 - 0.01 C_{r}) f_{y v} A_{v} h_{0}$	$\frac{ϕ_{f} A_{f} E_{f} ε_{f e} d_{f}}{s_{f}}$
AK. EL-SAYED^[12]	$0.17 λ \sqrt[]{f_{c}} b_{w, e f f} h_{0}$	$f_{y v} A_{w, e f f} h_{0}$	$\frac{ϕ_{f} A_{f, e f f} E_{f} ε_{f e} d_{f}}{s_{f}}$

新窗口打开| 下载CSV

上述研究虽尝试了各种不同的抗剪模型,但局限于自身试验数据的验证,或者试验数据有限,因此公式的适用性有待考证。并且认为混凝土、箍筋和FRP的抗剪贡献只是简单的叠加,从而忽略了FRP-箍筋-混凝土三者之间的相互影响。除此之外,试验数据仅限于细长梁,对于深梁的部分基本没有涉及。

3.2 不同模型之间的对比

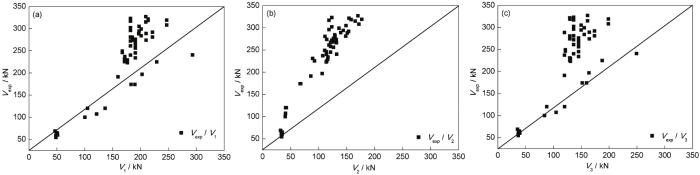
收集了现有的公开发表文献中关于FRP加固锈蚀箍筋混凝土梁共58组试验数据^[14-18],主要参数包括梁宽b,范围为119~250 mm；梁高h₀,范围为165~360 mm；剪跨比λ,范围为1.0~3.05；混凝土立方体抗压强度f_c',范围为20~40.5 MPa；梁的纵筋直径d的范围为18~28 mm；箍筋直径d_v的范围为6~10 mm；配箍率ρ_v为0.167~0.661%；FRP配布率ρ_f为0.053~1.829%；FRP的弹性模量E_f范围为95.8~235 GPa,利用试验数据对3.1中的3个计算模型进行了验证,结果显示上述提到的计算模型均严重低估了试验梁的承载力,如图5所示。

图5

图5 不同模型试验值与计算值对比

Fig.5 Test results of different models were compared with the calculated results: (a) V_exp/ V₁, (b) V_exp/ V₂, (c) V_exp/ V₃

利用本文得到的计算模型对试验数据进行计算后的结果如图6所示,表3列出了各模型的统计性结果。可以看出所收集的试验梁结果与本文计算模型的计算值比值的平均值更接近1,并且其方差最小,说明计算结果的离散性更小,因此进一步说明了本文计算模型的精确性和有效性。

图6

图6 本文模型计算值与试验值对比

Fig.6 Model results are compared with the test results

表3 不同模型离散指标对比

Table 3 Comparison of discrete indicators of different models

Model	EI- Maaddawy	Li	AK. EL-SAYED	Model of this paper
Average Value	1.33	2.15	1.77	1.04
Standard-Deviation	0.21	0.29	0.36	0.15
Coefficient of-Variation	0.16	0.13	0.20	0.15

新窗口打开| 下载CSV

4 结论

本文提出了基于简化修正压力场理论的FRP加固锈蚀箍筋混凝土梁的计算模型,并且收集了现有文献中的FRP加固锈蚀箍筋混凝土梁的试验数据以及现有的抗剪承载力计算模型,通过理论推导和计算分析,得出了以下结论：

(1) 本文基于简化修正压力场理论,考虑了截面面积损失、锈蚀箍筋的力学性能劣化等因素,建立了FRP加固的锈蚀箍筋混凝土梁的计算模型。

(2) FRP加固锈蚀箍筋混凝土梁的抗剪计算模型尚处于初步研究阶段,本文提出的模型相对于其他模型来说,能够更加准确地预测试验梁的抗剪承载力。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Zhu

, Cai

J S

, Hong

J X

, et al.

Effect of hydration response nanomaterials on corrosion resistance of reinforced concrete

[J]. J. Chin. Soc. Corros. Prot., 2021, 41: 732

朱哲, 蔡景顺, 洪锦祥等.

水化响应纳米材料对钢筋混凝土整体耐蚀性能影响

[J]. 中国腐蚀与防护学报, 2021, 41: 732

[2]

El-Sayed

A K

Shear capacity assessment of reinforced concrete beams with corroded stirrups

[J]. Constr. Build. Mater., 2017, 134: 176

DOI URL [本文引用: 2]

[3]

Zhao

Y X

State-of-art of corrosion-induced cracking of reinforced concrete structures

[J]. J. Southeast Univ. (Nat. Sci. Ed.), 2013, 43: 1122

赵羽习

钢筋锈蚀引起混凝土结构锈裂综述

[J]. 东南大学学报(自然科学版), 2013, 43: 1122

[4]

Chen

X D

, Zhang

, Gu

, et al.

Probability analysis on service life prediction of reinforced concrete structures

[J]. J. Chin. Soc. Corros. Prot., 2021, 41: 673

陈宣东, 章青, 顾鑫等.

基于概率分析的钢筋混凝土结构服役寿命预测研究

[J]. 中国腐蚀与防护学报, 2021, 41: 673

[5]

Huang

Z F

Coupling effect of shear failure modes and steel corrosion on shear behavior of RC beams shear-strengthened with EB-CFRP

[D]. Shenzhen: Shenzhen University, 2017

黄泽峰

不同剪切破坏模式下考虑箍筋锈蚀的CFRP加固梁的抗剪性能研究

[D]. 深圳: 深圳大学, 2017

[6]

Cairns

, Plizzari

G A

, Du

, et al.

Mechanical properties of corrosion-damaged reinforcement

[J]. ACI Mater. J., 2005, 102: 256

[7]

Zhang

W P

, Zhou

B B

, Gu

X L

, et al.

Probability distribution model for cross-sectional area of corroded reinforcing steel bars

[J]. J. Mater. Civ. Eng., 2014, 26: 822

DOI URL

[8]

El-Sayed

A K

, Hussain

R R

, Shuraim

A B

Influence of stirrup corrosion on shear strength of reinforced concrete slender beams

[J]. ACI Struct. J., 2016, 113: 1223

[9]

Higgins

, Farrow

W C III

, Potisuk

, et al.

Shear capacity assessment of corrosion-damaged reinforced concrete beams

[R]. Salem, Oregon: Oregon Department of Transportation, 2003

[10]

Zhao

Y X

, Jin

W L

Analysis on shearing capacity of concrete beams with corroded stirrups

[J]. J. Zhejiang Univ. (Eng. Sci.), 2008, 42: 19

赵羽习, 金伟良.

锈蚀箍筋混凝土梁的抗剪承载力分析

[J]. 浙江大学学报 (工学版), 2008, 42: 19

[11]

ACI Committee 440. Guide for the design and construction of externally bonded FRP systems for strengthening concrete structures

[R]. Farmington Hills, MI: American Concrete Institute, 2008

[12]

Vecchio

F J

, Collins

M P

The modified compression-field theory for reinforced concrete elements subjected to shear

[J]. ACI J. Proc., 1986, 83: 219

[13]

Bentz

E C

, Vecchio

F J

, Collins

M P

Simplified modified compression field theory for calculating shear strength of reinforced concrete elements

[J]. ACI Stuct. J., 2006, 103: 614

[本文引用: 3]

[14]

H M

, Wu

, Wang

Shear performance of reinforced concrete beams with corroded stirrups strengthened with carbon fiber-reinforced polymer

[J]. ACI Struct. J., 2016, 113: 51

[15]

El-Maaddawy

, Chekfeh

Shear strengthening of T-beams with corroded stirrups using composites

[J]. ACI Struct. J., 2013, 110: 779

[16]

Qin

S D

, Dirar

, Yang

, et al.

CFRP shear strengthening of reinforced-concrete T-Beams with corroded shear links

[J]. J. Compos. Constr., 2015, 19: 04014081

[17]

El-Sayed

A K

Shear capacity prediction for stirrup-corroded RC beams strengthened with FRP

[J]. Eng. Struct. Technol., 2019, 11: 32

[18]

Z W

, Zhang

W P

, Gu

X L

Modeling of shear behavior of reinforced concrete beams with corroded stirrups strengthened with FRP sheets

[J]. J. Compos. Constr., 2018, 22: 04018035