考虑应力比和门槛值的海水腐蚀疲劳裂纹扩展预测模型

doi:10.11902/1005.4537.2021.016

考虑应力比和门槛值的海水腐蚀疲劳裂纹扩展预测模型

刘冬¹^,², 刘静^,¹, 黄峰¹, 杜丽影², 彭文杰²

1.武汉科技大学省部共建耐火材料与冶金国家重点实验室武汉 430081

2.宝钢股份中央研究院武钢有限技术中心武汉 430080

Corrosion Fatigue Crack Growth Prediction Model Based on Stress Ratio and Threshold for Marine Engineering Steel DH36Z35 in Seawater

LIU Dong¹^,², LIU Jing^,¹, HUANG Feng¹, DU Liying², PENG Wenjie²

1.The State Key Laboratory of Refractories and Metallurgy, Wuhan University of Science and Technology, Wuhan 430081, China

2.R & D Center of Wuhan Iron & Steel Co. Ltd. , Baosteel Central Research Institute, Wuhan 430080, China

通讯作者: 刘静，E-mail：liujing@wust.edu.cn，研究方向为高性能钢铁材料及服役安全

收稿日期: 2021-01-22 修回日期: 2021-02-25 网络出版日期: 2021-11-05

基金资助:

国家自然科学基金. 51871172
中央指导地方科技发展专项. ZYDD2018026

Corresponding authors: LIU Jing, E-mail:liujing@wust.edu.cn

Received: 2021-01-22 Revised: 2021-02-25 Online: 2021-11-05

作者简介 About authors

刘冬，男，1985年生，博士生，高级工程师

摘要

采用自行改造的海水腐蚀疲劳试验机，研究了3 Hz频率、不同应力比R (0.1、0.3、0.5) 下，海洋工程用结构钢DH36Z35在空气和人造海水中疲劳裂纹扩展动力学行为。结果表明：相同裂纹尖端应力场强度因子幅值ΔK下，空气和海水环境中都显示疲劳裂纹扩展速率随着应力比R的增加而增加的规律，在近门槛值区间1×10^-7 mm/cycle≤da/dN≤1×10^-6 mm/cycle该现象尤其明显；在疲劳裂纹扩展速率da/dN＞1×10^-6 mm/cycle的中速区间，空气中和海水中疲劳裂纹扩展速率出现拐点，高于该拐点海水加速裂纹扩展，低于该拐点海水抑制裂纹扩展，且应力比R越大，拐点对应裂纹扩展速率越高。依据空气和海水中不同应力比和门槛值条件下疲劳裂纹扩展速率实验结果，提出了一种修正的Walker模型，可通过空气中疲劳裂纹扩展速率预测不同应力比下海水环境中疲劳裂纹扩展速率。

关键词： 海洋工程用结构钢 ; 腐蚀 ; 疲劳裂纹扩展速率 ; 应力比 ; 人造海水

Abstract

The fatigue crack growth rate of marine engineering structural steel DH36Z35 in air and artificial seawater are comparatively assessed by means of a home-made seawater corrosion fatigue machine by applied stress ratio of 0.1, 0.3 and 0.5 with a frequency of 3 Hz. The results show that the fatigue crack growth rate increases with the increase of stress ratio R under the same ΔK bothin air and artificial seawater, and this phenomenon is especially evident in the near threshold range 1×10^-7 mm/cycle≤da/dN≤1×10^-6 mm/cycle. When the fatigue crack growth rate (da/dN) is above 1×10^-6 mm/cycle, a flection point may emerge on the curve of fatigue crack growth rate measured both in air and seawater. For the case of testing in the seawater, above the flection point the crack growth is accelerated, whereas below which the crack growth is inhibited. The higher the stress ratio is, the higher the fatigue crack rate corresponding to the inflection point is. Based on the difference of test results in air and artificial seawater by different stress ratio and threshold, a modified Walker model for the prediction of corrosion fatigue crack growth rate is established. By the new prediction model, the fatigue crack growth rate by the applied different stress ratio in seawater can be predicted through the fatigue crack growth rate in air.

Keywords： marine engineering structural steel ; corrosion ; fatigue crack growth rate ; stress ratio ; artificial seawater

PDF (2197KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘冬, 刘静, 黄峰, 杜丽影, 彭文杰. 考虑应力比和门槛值的海水腐蚀疲劳裂纹扩展预测模型. 中国腐蚀与防护学报[J], 2022, 42(1): 163-168 DOI:10.11902/1005.4537.2021.016

LIU Dong, LIU Jing, HUANG Feng, DU Liying, PENG Wenjie. Corrosion Fatigue Crack Growth Prediction Model Based on Stress Ratio and Threshold for Marine Engineering Steel DH36Z35 in Seawater. Journal of Chinese Society for Corrosion and Protection[J], 2022, 42(1): 163-168 DOI:10.11902/1005.4537.2021.016

海洋工程结构如海洋钻井平台、海底油气管线等在长期服役过程中，除了经受到海水及海洋大气腐蚀^[1,2]外，还常受到风载、雪载、流载以及海浪冲击等动态载荷作用，产生疲劳损伤。腐蚀疲劳过程中疲劳裂纹扩展是主要的破坏形式，腐蚀疲劳裂纹扩展是一种十分复杂的物理行为，腐蚀环境、力学条件等诸多因素都会不同程度地影响腐蚀疲劳裂纹扩展和寿命评估。

Matlock等^[3]开展了海洋工程结构焊接接头海水腐蚀疲劳裂纹扩展特性影响因素研究，测试了ASTM A36钢焊接接头在0.3和30 Hz下裂纹扩展速率，低频率下裂纹扩展速率明显加速。Adedipe等^[4]比较了S355J2+N钢在海水环境下应力比R=0.1和0.5的腐蚀疲劳裂纹扩展速率，应力比越高裂纹扩展速率越快，并建立了不同应力比对应裂纹尖端张开时间模型。李新宇等^[5]研究了2B25铝合金在3.5%NaCl溶液和1%油箱积水溶液中的腐蚀疲劳性能，对比发现3.5% (质量分数) NaCl溶液对实验件腐蚀疲劳性能的影响更为显著。Meng等^[6]研究了7075铝合金腐蚀疲劳裂纹扩展速率影响因素，进行了铝合金在pH3、7、10的3种海水溶液中的腐蚀疲劳试验，结果显示，pH越高，裂纹扩展速率越慢。腐蚀环境中腐蚀成分、pH等对于腐蚀疲劳裂纹扩展影响也十分明显，可见，力学条件中频率、应力比等，以及腐蚀环境中化学成分、pH等对da/dN存在一定影响，针对某些特定钢种需要考虑服役环境和加载条件综合作用下的腐蚀疲劳动力学行为。

另外，疲劳裂纹扩展速率da/dN-ΔK曲线是工程结构损伤容限设计与分析过程中的重要依据。国内外不少专家学者做过深入探讨，最早采用的数学模型为Paris模型da/dN=C(ΔK)^m[7]。还有很多考虑其它影响因素的预测模型，譬如在空气介质中开展试验时，考虑门槛值ΔK_th影响的Trantina-Johnson模型da/dN=C(ΔK-ΔK_th)^m[8]，考虑应力比R影响的Walker模型da/dN=C(ΔK)^m $_{1}$ (1-R)^m $_{2}$ ^[9,10]，以及考虑R和平面应变断裂韧性K_c的Forman模型da/dN= $\frac{C {(Δ K)}^{m}}{(1 - R) K_{C} - Δ K}$ ^[11]。Wang等^[12-14]对铝合金进行腐蚀疲劳试验，提出了一种门槛值模型的多项式拟合模型(da/dN)_cf=Bcf(ΔK-ΔK_thcf)²。

以上这些模型考虑了诸多影响因素，可通过一种特定影响因素条件下的da/dN实验，预测影响因素变化后不同实验条件下的da/dN，可以大大减少开展这种实验难度大、检验费用昂贵的腐蚀疲劳实验的频次。但以上预测模型均是依据空气介质或者腐蚀介质某一影响因素变化提出的，如果通过研究腐蚀介质中da/dN与空气介质中差异，再考虑腐蚀环境或者力学条件等影响因素变化对da/dN速率的影响，提出一种依据空气介质中特定实验条件下da/dN预测相同条件下海水介质中da/dN的模型，则可以仅开展空气介质中da/dN实验，从而得到腐蚀介质中疲劳裂纹扩展动力学特征，这样更有利于开展腐蚀环境下da/dN研究，对于工程人员的损伤容限设计将提供更多便利条件。

本文以海洋工程结构用钢DH36Z35为研究对象，在GB/T6398-2017中提供的模仿真实海水环境的人造海水中开展不同应力比下da/dN，并与空气中相应结果进行对比分析，研究空气中和海水中应力比对da/dN的影响规律，以及与空气中da/dN差异规律。提出了一种新的与应力比和门槛值相关的预测da/dN修正walker模型，可以通过空气介质中da/dN-ΔK曲线预测海水腐蚀环境下的da/dN-ΔK曲线，为该钢种的应用和寿命预测提供理论依据和数据支持。

1 腐蚀疲劳裂纹扩展速率实验

实验材料选用DH36Z35钢，试样尺寸参照GB/T 6398-2017，如图1所示。实验用DH36Z35钢化学成分 (质量分数，%) 为：C 0.13，Si 0.20，Mn 1.10，P 0.015，Ni 0.025，Cr 0.01，S 0.003，Cu 0.01，Fe余量。力学性能为：R_eL=392 MPa，R_m=534 MPa，A=31.0%， $K_{V_{2}}$ =276 J。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 腐蚀疲劳裂纹扩展速率试样图

Fig.1 Schematic diagram of corrosion fatigue crack growth rate sample (mm)

da/dN测试在液压伺服材料试验机 (MTS810) 上按照GB/T6398-2017进行，频率为3 Hz，R选择0.1，0.3和0.5。采用降K控制，梯度K=-0.1，初始最大应力场强度因子为K_max=50 MPa·m^1/2，波形为正弦波，环境温度为 (20±3) ℃。实验环境包括空气介质和人造海水环境，人造海水化学成分 (g/L) 为：NaCl 24.5，Na₂SO₄ 4.1，MaCl₂·6H₂O 11.1，CaCl₂1.2，SrCl₂·6H₂O 0.042，KCl 0.69，NaHCO₃ 0.2，KBr 0.1，H₃BO₃ 0.027，NaF 0.003。为实现海水循环流动、流速可控、温度可控等实验模拟条件，实验在自行设计的海水循环模拟系统上进行。

2 结果与讨论

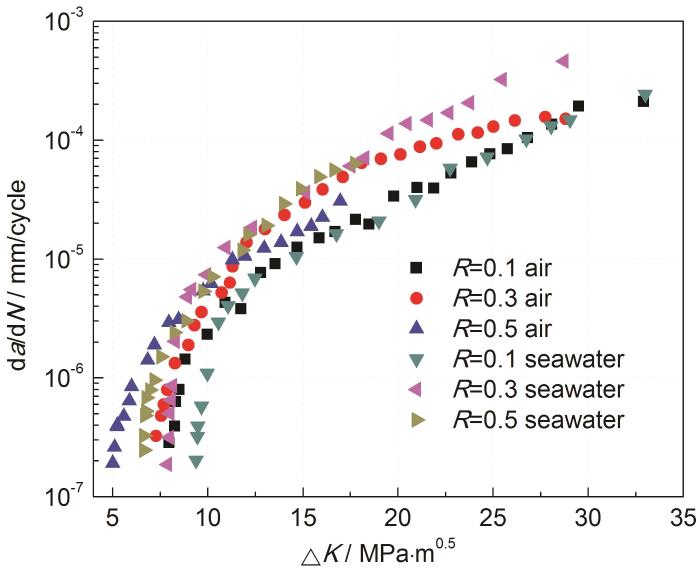
图2给出了DH36Z35钢在空气和人造海水中，不同R=0.1，0.3和0.5下疲劳裂纹扩展动力学曲线。在上述两种环境介质条件下，DH36Z35钢试样da/dN均随着应力比R的增加而增加，且该现象在近门槛值区间尤其明显。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 空气及海水中不同应力比下疲劳裂纹扩展速率

Fig.2 Fatigue crack growth rate test underdifferent stress ratios in air and in seawater

为了进一步确认海水腐蚀环境对疲劳裂纹扩展速率的影响，对比不同R下空气中和海水中da/dN如图3所示。图3a中，R=0.1时空气中和海水中da/dN曲线在1×10^-7 mm/cycle≤da/dN≤1×10^-6 mm/cycle近门槛值区间差别较大，空气中da/dN大于海水中，但在da/dN＞1×10^-6 mm/cycle的中速区间两种环境下曲线基本重合。随着应力比的不断增加，空气中和海水中中速区da/dN曲线差异越发明显，不再重合。

图3

新窗口打开| 下载原图ZIP| 生成PPT

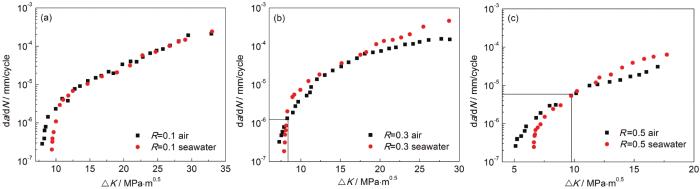
图3 R=0.1，0.3和0.5时空气和海水中da/dN-ΔK曲线

Fig.3 da/dN-ΔK curves under R =0.1 (a), 0.3 (b) and 0.5 (c) in air and seawater

图3b中，R=0.3时在da/dN＞1×10^-6 mm/cycle的中速区间，空气中和海水中da/dN曲线出现拐点，拐点da/dN约为5×10^-5 mm/cycle，低于该拐点，空气中da/dN高于海水中；高于该拐点，海水中da/dN高于空气中。图3c中，R=0.5时海水中与空气中曲线差异愈发明显，拐点da/dN约为3×10^-5 mm/cycle，R=0.5时空气中和海水中da/dN曲线出现拐点最为明显。低于该拐点速率，海水介质对da/dN起阻滞作用，高于该拐点速率，海水介质对da/dN起加速作用。

有些学者认为氢致开裂是高强钢材料腐蚀疲劳裂纹扩展的主要机制。韩恩厚等^[15]认为金属材料腐蚀疲劳过程中溶液中H⁺扩散至裂纹尖端前缘区域，发生还原反应，产生吸附H原子，H原子在裂纹尖端塑性区富集达到临界值后，裂尖原子结合力会减小导致局部裂纹萌生，加速外载荷作用下的疲劳裂纹扩展。Jones等^[16]认为塑性变形受裂纹增多的影响或者氧化膜和腐蚀产物的干扰，在循环拉伸过程中裂纹表面会提前接触发生闭合，导致实际有效ΔK_eff小于计算所得的ΔK，从而使裂纹扩展速率明显减低，这种现象在接近门槛值的低应力区间尤其明显。Elber^[17]已经通过实验证实了裂纹尖端塑性区对疲劳裂纹闭合现象的影响。由于裂纹闭合作用，裂纹扩展的驱动力由ΔK=K_max-K_min变为ΔK_eff=K_max-K_op，其中K_op为在裂纹闭合下，能使裂纹扩展的最小应力强度因子，只有当应力强度因子大于K_op时裂纹才能张开，使得裂纹发生扩展。李松梅等^[18]在开展AerMet100钢腐蚀疲劳裂纹扩展时也发现了在da/dN≥1×10^-5 mm/cycle时腐蚀环境会加速疲劳裂纹扩展，在da/dN＜1×10^-5 mm/cycle时由于裂尖闭合效应腐蚀环境会降低da/dN。进一步证明本文发现随裂尖应力场强度因子增加，腐蚀对疲劳裂纹扩展影响存在拐点的现象是存在的。

但本文通过不同应力比的实验，进一步提出了该拐点不是固定值，而是随应力比增加而提高的。裂纹闭合解除对应裂尖最小应力强度因子K_op一定，应力比越大，裂纹开始张开对应的K_max也越大，有效裂纹扩展的驱动力ΔK_eff也就越大，拐点对应的裂纹扩展速率也就越快，因此，拐点裂纹扩展速率是随应力比增加而提高的。

根据Paris模型拟合图3中各曲线方程如表1所示，其中r为拟合曲线方程相关性系数。曲线方程数据处理及门槛值ΔK_th的计算与GB/T6398-2017中推荐方法一致。

表1 Paris模型拟合曲线方程及门槛值ΔK_th

Table 1 Paris model fitting curve equation and the threshold value Δ K_th

No.	Environment	R	C	m	r	ΔK_th
S01	Air	0.1	4.313×10^-10	3.767	0.989	7.49
S02	Air	0.3	3.645×10^-10	4.054	0.986	6.54
S03	Air	0.5	4.088×10^-9	3.128	0.993	4.41
S04	Seawater	0.1	4.712×10^-10	3.733	0.972	9.15
S05	Seawater	0.3	2.631×10^-10	4.248	0.953	7.79
S06	Seawater	0.5	1.690×10^-10	4.538	0.961	6.07

新窗口打开| 下载CSV

如果考虑门槛值ΔK_th对疲劳裂纹扩展速率的影响，以裂纹尖端应力场强度因子幅值ΔK与门槛值ΔK_th的差值ΔK-ΔK_th为x轴，da/dN为y轴，构造不同应力比下空气和海水中da/dN变化曲线，如图4所示。采用Trantina-Johnson模型拟合各曲线方程如表2所示。对比表2中数据，考虑门槛值ΔK_th的影响后，不同应力比下拟合曲线的系数C更加统一，在相同环境下在同一数量级，且拟合曲线相关性系数r更高。

图4

新窗口打开| 下载原图ZIP| 生成PPT

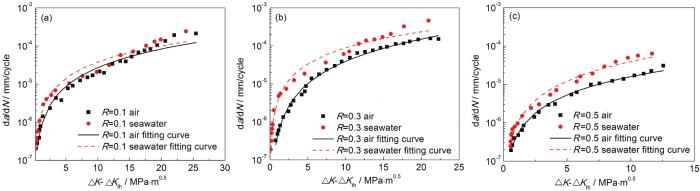
图4 R=0.1，0.3和0.5时空气和海水中da/dN-(ΔK-ΔK_th) 曲线

Fig.4 da/dN-(ΔK-ΔK_th) curves underr R=0.1 (a), 0.3 (b) and 0.5 (c) in air and seawater

表2 Trantina-Johnson模型拟合曲线方程

Table 2 Trantina-Johnson model fitting curve equation

No.	Environment	R	C	m	r
S01	Air	0.1	6.379×10^-7	1.628	0.986
S02	Air	0.3	4.051×10^-7	1.995	0.997
S03	Air	0.5	4.195×10^-7	1.581	0.996
S04	Seawater	0.1	1.480×10^-6	1.410	0.975
S05	Seawater	0.3	2.576×10^-6	1.425	0.993
S06	Seawater	0.5	8.343×10^-7	1.673	0.992

新窗口打开| 下载CSV

R对da/dN的影响在本研究中相对门槛值更加显著，若在考虑门槛值的基础上进一步考虑应力比的影响，并以空气介质中da/dN实验结果为依据，预测海水腐蚀环境下的da/dN，就必须将数学模型Trantina-Johnson模型和Walker模型合并考虑，得到新的修正后Walker模型：

{(\frac{d a}{d N})}_{c o r} = C_{R} \times C_{a i r} \times {(Δ K - Δ K_{t h})}^{m_{a i r}} {(1 - R)}^{n}

(1)

其中， ${(\frac{d a}{d N})}_{c o r}$ 为海水腐蚀环境下的疲劳裂纹扩展速率，C_air和m_air为空气介质中da/dN曲线方程的物理常数；假定R影响系数为f(R)=C_R(1-R)ⁿ，其中自变量为 (1-R)，C_R为幂函数系数，n为幂函数指数。分别计算了不同ΔK-ΔK_th下海水与空气中da/dN的比值f(R)，并求得了不同应力比下f(R) 的平均值。以f(R) 的平均值与 (1-R) 构造幂函数，通过幂函数拟合可以得到，C_R=1.368，n=-0.849。

依据空气中da/dN实验结果预测海水中da/dN的数学模型为：

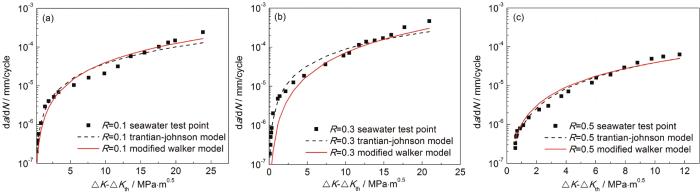
{(\frac{d a}{d N})}_{c o r} = 1.368 \times C_{a i r} \times {(Δ K - Δ K_{t h})}^{m_{a i r}} {(1 - R)}^{- 0.849}

(2)

图5分别为海水环境中不同R下da/dN实测值，以及采用Trantian-Johnson模型和修正后Walker模型计算的预测值的对比图。通过计算，R=0.1，0.3和0.5下，采用Trantian-Johnson模型的预测值与实测值相对偏差的平均值分别为4.82%，6.41%和1.21%。采用修正后Walker模型的预测值与实测值相对偏差的平均值分别为5.51%，8.82%和4.07%。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 R=0.1，0.3和0.5时海水中da/dN实测值与预测值比较图

Fig.5 Measured and predicted da/dN under R=0.1 (a), 0.3 (b) and 0.5 (c) in seawater

Trantian-Johnson模型预测基础数据为海水环境下某一门槛值条件下da/dN实验结果，相对传统Paris模型只能在考虑海水环境下门槛值不同时，提升海水环境中疲劳裂纹扩展精度。但本文提出的修正后Walker模型预测的基础数据为空气介质中的da/dN实验结果，再考虑了门槛值和应力比的综合影响，可依据空气介质中da/dN预测海水环境下不同应力比和门槛值条件下的da/dN。总体来看，修正后Walker模型的预测精度略低于已被证实的Trantian-Johnson模型，但应用价值更大，可节省大量海水环境下繁琐复杂da/dN实验的过程，加速工程结构损伤容限设计效率。且当在da/dN大于1×10^-6 mm/cycle时，R=0.1，0.3和0.5下，采用修正后Walker模型的预测值与实测值相对偏差的平均值仅为2.95%，3.17%和1.14%，修正后Walker模型比Trantian-Johnson模型与实测点相关性更好。

3 结论

(1) 空气和海水环境中，实验应力比范围内， DH36Z35钢da/dN均随着R的增加而增加；海水环境下，近门槛值区间应力比对裂纹扩展速率影响更加显著。

(2) 不同应力比下，海水与空气中da/dN存在拐点，低于该拐点，海水介质对da/dN起阻滞作用，高于该拐点，海水介质对da/dN起加速作用。而且该拐点是随R增加而提高的。

(3) 依据空气介质中da/dN实验结果，考虑R和ΔK_th对da/dN的影响，建立了一种修正的Walker模型。在R=0.1，0.3和0.5下，采用修正后Walker模型的预测值与实测值相对偏差的平均值分别为5.51%，8.82%和4.07%，与Trantian-Johnson模型精度相当，但可依据空气介质中da/dN预测海水环境下不同R和ΔK_th条件下的da/dN，比依据海水中某一特定条件下da/dN实验结果预测条件改变后海水da/dN的模型更具实用价值。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Liu

, Wang

Environmental impact of material corrosion research progress in marine splash zone

[J]. J. Chin. Soc. Corros. Prot., 2010, 30: 504