中国腐蚀与防护学报 2016 , 36 (4): 370-374 https://doi.org/10.11902/1005.4537.2015.152

研究报告

基于Gumbel极值I型分布埋地油气管道的剩余寿命预测

张新生, 曹乃宁, 李亚云

西安建筑科技大学管理学院西安 710055

Residual Life Prediction of Buried Oil and Gas Pipelines Based on Gumbel Extreme Value Type I Distribution

ZHANG Xinsheng, CAO Naining, LI Yayun

School of Management, Xi'an University of Architecture and Technology, Xi'an 710055, China

中图分类号: TE88

文献标识码: A

文章编号: 1005-4537(2016)04-0370-05

通讯作者: 通讯作者：张新生,E-mail：xinsheng.zh@outlook.com,研究方向为管道风险评估与管理及智能信息处理等

基金资助: 国家自然科学基金项目 (61271278),陕西省社会科学基金项目(2015R13)和陕西省自然科学基金项目 (2016JM6023) 资助

作者简介:

作者简介：张新生,男,1978年生,博士,副教授

展开

摘要

基于Gumbel极值I型分布,对在线检测原始数据进行处理,建立油气管道最大腐蚀深度预测模型,确定整条油气腐蚀管道可能存在的最大腐蚀深度;以此建立管道剩余壁厚模型,来预测油气管道的剩余寿命;最后以国内的某一管道为例,将该模型应用于整条管道的剩余寿命预测中,预测结果为19.95 a,表明该方法预测的结果是合理的。

关键词： 油气管道腐蚀 ; 最大腐蚀深度 ; 剩余寿命预测 ; Gumbel极值I型分布 ; Markov链Monte ; Carlo模拟

Abstract

Original corrosion data, which were acquired by online detecting a buried oil and gas pipeline, were processed in accord with the Gumbel extreme value type I distribution, then a model for predicting the maximum corrosion depth is built to determine the possible maximum corrosion depth of the whole pipeline with the above method, a model for predicting the residual thickness of pipe wall is established to predict the residual life of oil and gas pipelines. In the end, as an example, the model was used to predict the residual life of a domestic pipeline in service, it is ca 19.95 a, which indicates that the predict result is correct and reasonable.

Keywords： oil and gas pipeline corrosion ; maximum depth of corrosion pit ; residual life prediction ; Gumbel extreme value type I distribution ; Markov chain Monte Carlo simulation

PDF (2053KB) 元数据多维度评价相关文章收藏文章

本文引用格式导出 EndNote Ris Bibtex

张新生, 曹乃宁, 李亚云. 基于Gumbel极值I型分布埋地油气管道的剩余寿命预测[J]. , 2016, 36(4): 370-374 https://doi.org/10.11902/1005.4537.2015.152

ZHANG Xinsheng, CAO Naining, LI Yayun. Residual Life Prediction of Buried Oil and Gas Pipelines Based on Gumbel Extreme Value Type I Distribution[J]. 中国腐蚀与防护学报, 2016, 36(4): 370-374 https://doi.org/10.11902/1005.4537.2015.152

1 前言

近年,随着油气管道使用年限的增加,越来越多的油气管道带缺陷工作,特别是由于腐蚀造成的管道缺陷越来越严重,管道腐蚀失效引起的管道穿孔、泄漏事故频率也在不断上升,给社会和企业造成巨大的经济损失。因此,研究腐蚀对管道结构完整性的危害程度,预测油气管道剩余寿命确保管道安全运行具有重要的研究意义。

目前,国内外学者对油气管道剩余寿命的预测进行了研究,如国外学者Kleiner^[1]利用Markov模型建立了管道寿命预测模型;俞树荣等^[2]采用Monte Carlo方法计算以Shell-92确定性模型为基础所建立的管道腐蚀剩余寿命预测概率模型,计算出了管道剩余寿命;陈典斌等^[3]以灰色理论GM (1,1) 模型为基础,建立腐蚀管道可靠性模型并使用VB进行腐蚀管道剩余寿命分析。采用这些研究方法得到的结果与实际值较接近,但是仍存在不足。油气管道的腐蚀速率并不是固定的,而是随着时间变化的,因此,认为腐蚀速率为固定值预测出的管道剩余寿命还是存在较大误差的。

本文将基于Gumbel极值I型分布的统计方法构建油气管道剩余寿命预测模型,通过分析已知管道腐蚀在线检测数据,建立油气管道的最大腐蚀深度预测模型并进行预测,最终预测出油气管道剩余寿命。

2 极值I型分布

对于有腐蚀缺陷的管道,缺陷类型通常为均匀腐蚀、局部腐蚀和点蚀^[4]。而影响管道使用寿命的主要因素是点腐蚀,因为引起管道穿孔破坏的是最深的蚀孔,一旦管道穿孔,管道就发生泄漏失效事故,因此,最大的腐蚀坑深度是评定穿孔破坏的重要指标^[5]。由于油气管道工作环境复杂,其腐蚀过程的规律难以掌握,通过建立统一的数学公式来表示各腐蚀因素的影响规律是比较困难的^[6,7]。统计方法是通过统计分析管道最大腐蚀深度,通过计算腐蚀失效概率来预测管道剩余寿命^[8,9]。极值I型分布是观测值中最大值或最小值的概率分布,是概率统计方法中的一个重要分支,广泛应用于许多工程实际问题的分析、评估中。

对于观测值的最大值或最小值的集合进行统计的极值I型分布形式如下：

$\begin{matrix} F_{Ι} (y) = \exp (- \exp (- \frac{x - λ}{α})), x \in (- \infty, \infty); \end{matrix}$

$\begin{matrix} λ \in (- \infty, \infty); α > 0 \end{matrix}$ (1)

此即Gumbel极值I型分布中的最大值分布,又称为Gumbel极值I型分布,其中,F_I(y) 为最大值不超过x的概率,x为某一随机变量的最大值;α为尺度参数,λ为位置参数。

$\begin{matrix} F_{Ι} (y) = 1 - \exp (- \exp (- \frac{x - λ}{α})), x \in (- \infty, \infty); \end{matrix}$

$\begin{matrix} λ \in (- \infty, \infty); α > 0 \end{matrix}$ (2)

此即Gumbel极值I型分布中的最小值分布,其中F_I(y) 为最小值不超过x的概率,x为某一随机变量的最小值。

管道腐蚀缺陷的概率分布有一定的规律,例如,应力腐蚀破裂寿命符合Weibull分布,管道腐蚀增长量符合逆Gaussian分布,管道腐蚀点数符合Possion分布等^[5]。学者经过大量的实验数据分析^[10-13]认为,油气管道的局部腐蚀的最大腐蚀点的概率分布服从Gumbel极值I型分布函数。

3 基于极值I型分布的管道最大腐蚀深度预测

3.1 极值I型分布应用于埋地油气管道腐蚀剩余寿命的预测

极值I型分布用于油气管道腐蚀剩余寿命预测的基本步骤如下：(1) 获取腐蚀严重区段的管道腐蚀数据;(2) 将获得的数据通过数理统计方法计算最大腐蚀深度的分布概率利用图形检验的方法来检验最大腐蚀深度符合极值分布是否合理;(3) 若符合极值分布,则构造统计分析模型;(4) 利用Markov链Monte Carlo (MCMC) 仿真估计模型参数;(5) 基于极值I型分布获得整条管道可能的最大腐蚀深度;(6) 由APIRP579^[14]推荐的公式求出腐蚀管道的临界腐蚀深度;(7) 最终基于所得最大腐蚀深度和临界腐蚀深度建立剩余寿命预测模型来预测油气管道的剩余寿命。油气管道腐蚀剩余寿命预测的基本步骤如图1所示。

显示原图| 下载原图ZIP| 生成PPT

图1 剩余寿命预测步骤流程图

Fig.1 Flow chart of residual life prediction

3.2 油气管道最大腐蚀深度预测模型

管道的局部腐蚀最大值的概率分布符合Gumbel极值I型分布,其分布函数依据式 (1) 为：

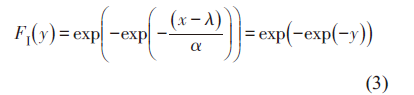
式中,F_I(y)为最大腐蚀深度不超过x的概率;x为最大腐蚀深度的随机变量;λ为统计参量,表示概率密度最大的腐蚀点深度;α为统计变量,表示腐蚀点深度的平均值;变量代换为y=(x-λ)/α。

由于油气管道埋在地下,在收集管道腐蚀坑深度数据时,不可能将整条管道开挖,采集所有腐蚀信息,这样工程量巨大难以实现且成本高。通常情况,工程上将管道外防腐层检测严重的区域进行开挖,进行取样收集数据。这样获得的最深的腐蚀深度存在很大的随机性,能够反映整个管道的腐蚀情况。将检测的数据进行统计处理,得到统计参量α和λ,然后根据式 (3) 计算最深的腐蚀深度不超过某一数值的概率。

假设有N个腐蚀深度x,这些腐蚀深度均是来自于处于相同环境的同一条管道的管段上的最大腐蚀深度点,将N个在同样条件下测得的最大腐蚀坑深度数据由小到大排序,标出序号i和对应的腐蚀坑深度值x_i,计算累积分布函数：

$\begin{matrix} F (y_{i}) = \frac{i}{N} + 1, (i = 1,2, 3, \dots, N) \end{matrix}$ (4)

将式 (3) 两端同时取2次对数,得：

$\begin{matrix} y = - \ln [- \ln \frac{1}{F_{Ι} (x)}] = \frac{(x - λ)}{α} \end{matrix}$ (5)

获得统计参量α和λ,代入到式 (3) 就可以求出最大腐蚀深度不超过某一数值的概率F(X≤x)。以x_i为横坐标, $\begin{matrix} - \ln [- \ln \frac{1}{F_{Ι} (x_{i})}] \end{matrix}$ 为纵坐标,将各点 ( $\begin{matrix} x_{i} \end{matrix}$ , $\begin{matrix} - \ln [- \ln \frac{1}{F_{Ι} (x {}_{i})}] \end{matrix}$ ) 画在直角坐标系中,如果这些点呈现线性关系,说明这些腐蚀数据服从Gumbel极值I型分布,然后进行统计参量估计。

回归周期T(x)与累计概率F_I(y) 的关系为：

$\begin{matrix} T (x) = \frac{1}{(1 - F_{I} (y))} \end{matrix}$ (6)

回归周期是某测定值x_i为观测顺序号的期待值。即抽取N个样本,其最大值意味着从少量小段的试样最大坑深推算出的整个局部段的坑深。

$\begin{matrix} T (x) = \frac{L}{N} \end{matrix}$ (7)

根据式 (7) 就可以得到整条L长管道大致的最大腐蚀坑深度。将式 (6) 求得的F(x)值代入式 (5) 可求得y值;最后将y值代入拟合直线方程可以求出最大局部腐蚀坑深度。管道腐蚀段L中的最大腐蚀点深度的预测值x_m为：

$\begin{matrix} x_{m} = x = λ + αy \end{matrix}$ (8)

3.3 预测模型参数的估计

利用MCMC模拟对油气管道最大腐蚀深度预测模型的参数进行估计,在无信息先验分布下,用MCMC专用软件包OpenBUGS对预测模型参数进行估计。

经过对大量的实验数据分析研究发现^[10-13],油气管道的局部腐蚀的最大腐蚀点服从Gumbel极值I型分布函数,即x~Gumbel(α,λ)。考虑到Gamma分布能够保证α和λ为正值且可以方便的作为一个无信息分布,本文选取Gamma分布作为α和λ的先验分布,即α~Gamma(p₁,q₁),λ~Gamma(p₂,q₂),其中,p₁(q₁)和p₂(q₂)分别表示α和λ的Gamma分布形状参数。

MCMC方法模拟的样本为10000个,对Gumbel极值I型分布进行Gibbs抽样,获得参数的Gibbs迭代轨迹 (trace) 和迭代历史 (history),根据大量的参数估计值的趋势收敛情况,确定估计参数的准确性。

3.4 腐蚀管道的临界腐蚀深度的计算

腐蚀管道的临界腐蚀深度的计算可由APIRP579^[14]推荐的公式求出：

$\begin{matrix} h_{\max} = \frac{PD}{2 F σ_{ys} E} \end{matrix}$ (9)

$\begin{matrix} Δh = h - h_{\max} \end{matrix}$ (10)

式中,h_max是管道临界腐蚀深度,mm;P是管道运行内压,MPa;D是管道公称直径,mm;F为设计系数,与管线所处地区类别相关;σ_ys是管材最小屈服强度,MPa;E是管材弹性模量,MPa;h是管道公称壁厚,mm; $\begin{matrix} Δ \end{matrix}$ h是管道允许腐蚀深度,mm。

4 油气管道腐蚀剩余寿命预测

实际油气管道的腐蚀并不是按照固定的腐蚀速度进行的,一般腐蚀程度会随着时间的增加而递增,但是腐蚀速率会随着腐蚀深度的增长而减小。根据腐蚀深度与使用年限的关系,利用工程上的经验公式来近似模拟管道最大腐蚀深度与使用年限的关系^[14],预测管道的使用寿命,从而确定管道的剩余寿命,如下式所示：

$\begin{matrix} t_{f} = {(\frac{Δh}{p})}^{\frac{1}{c}} t \end{matrix}$ (11)

式中,t_f为预测的管道设计使用寿命,a;t为管道服役时间,a;p为t时刻测到的最大腐蚀深度,mm;c为时间常数,由腐蚀体系等因素决定,只有一个时间测量值时,通常采用比较保守的值为0.5^[15]。

5 应用实例

辽宁某陆上油田集油管道已经运行了约10 a,管道规格为D273 mm×8(9) mm,油气管道材质为X52钢,管道外径D=273 mm,管道壁厚取较小值8 mm,屈服强度σ_ys=290 MPa,该管道工作压力P=0.85 MPa,不考虑地区类别,设计系数取1,即按照100%屈服强度计算,管材安全系数取1.1。该管道总长为3.6 km。工作者针对外防腐层检测腐蚀严重区域开挖,分段获取数据,检测时每km作为一个检测段,划分为21个段,每段随机检测60个点,在每个检测段上找出最深的腐蚀深度见表1。

表1 局部管道最大腐蚀深度

Table 1 Maximum partial corrosion depth

Intervals of maximumpartial corrosion depth	Number of maximumpartial corrosion depth / mm
(0.5, 1.0]	2
(1.0, 1.5]	10
(1.5, 2.0]	5
(2.0, 2.5]	3
(2.5, 3.0]	1

新窗口打开

5.1 油气管道最大腐蚀深度模型的验证

取到各段检测的最大腐蚀深度代入式 (5)~(7) 计算出各点的y,以x_i为横坐标,y_i为纵坐标,绘制直角坐标图并进行线性拟合,如图2所示。线性拟合度R²=0.982 (R²越接近1,说明越接近线性),说明局部腐蚀管道中所获取的最大腐蚀深度值与y有线性关系,这也正说明了腐蚀深度的概率服从Gumbel极值I型分布。

显示原图| 下载原图ZIP| 生成PPT

图2 最大腐蚀深度概率分布

Fig.2 Probability distribution of the maximum corrosion depth

5.2 油气管道剩余寿命预测

根据实例中提供的数据,采用MCMC方法来估计油气管道最大腐蚀深度预测模型的参数,MCMC估计参数结果α=1.323,λ=0.41。

MCMC方法对预测模型进行Gibbs抽样,得到预测模型参数的Gibbs迭代轨迹和迭代历史,其中,迭代轨迹随机选择第9800~10000个样本进行迭代,如图3~5所示。

显示原图| 下载原图ZIP| 生成PPT

图3 参数α和λ的迭代轨迹

Fig.3 Iterative trace of parameters α (a) and λ (b)

显示原图| 下载原图ZIP| 生成PPT

图4 参数α和λ的迭代历史

Fig.4 Iterative history of parameters α (a) and λ (b)

显示原图| 下载原图ZIP| 生成PPT

图5 参数α和λ的置信度

Fig.5 Confidencial level of parameters α (a) and λ (b)

显示原图| 下载原图ZIP| 生成PPT

图6 管道剩余寿命预测

Fig.6 Prediction of pipeline residual life

由图3和4所示获得的参数α和λ的迭代轨迹和迭代历史基本趋于稳定,认为迭代过程已经收敛。迭代收敛后,通过MCMC方法得到参数α和λ的置信度图形见图5。两个参数的分布区间与迭代历史区间基本符合,由此对两参数做出综合推断,从而估计出模型参数。

MCMC方法得到的模型参数α和λ的标准差分别为0.0977和0.0781,且迭代轨迹和迭代历史基本趋于稳定,可知MCMC估计参数是比较精确的。因此,通过软件模拟,估计参数α=1.323,λ=0.41,则由式 (8) 得管道最大腐蚀深度x_m=1.323+0.41y。

由式 (8)~(10) 得x_m=4.32 mm;由式 (9) 得管道临界腐蚀深度h_max=0.44 mm,由式 (10) 得最大允许腐蚀深度 $\begin{matrix} Δ \end{matrix}$ h =7.56 mm,将预测的最大腐蚀深度x_m和 $\begin{matrix} Δ \end{matrix}$ h 带入式 (11) 得管道的可使用寿命t_f=30.63 a;整条管道的腐蚀剩余寿命T=30.63-10.68=19.95 a。

国外油气管道的设计寿命一般为33 a^[16],显然以Gumbel极值I型分布预测出最大腐蚀深度为基础所计算出的管道使用时间30.63 a是合理的。说明通过利用概率统计的方法预测出油气管道的剩余寿命为19.95 a,与该油气管道的整个寿命期限比较,是合理的。

6 结论

(1) 依据管道局部挖坑在线检测数据所得的最大腐蚀深度概率分布,与Gumbel分布能够较好的拟合,油气管道的局部腐蚀的最大腐蚀深度的概率分布服从Gumbel极值I型分布函数。

(2) 用Gumbel极值I型分布预测出埋地油气管道的最大腐蚀深度,并估算出管道的剩余寿命。实例表明获取到的预测值确定的管道剩余寿命是合理的。

(3) Gumbel极值I型分布管道剩余寿命预测模型能够较精确的预测油气管道剩余寿命。

The authors have declared that no competing interests exist.

〈

〉