基于全局与局部误差融合的集成腐蚀速率预测模型：一种稳健优化策略

doi:10.11902/1005.4537.2024.242

基于全局与局部误差融合的集成腐蚀速率预测模型：一种稳健优化策略

郑文培¹^,²^,³, 刘迎正^,¹^,²^,³, 张娅茹¹^,²^,³, 周涛涛¹^,²^,³, 李兴涛⁴, 禹胜阳⁴, 蒋璐朦⁴

1.中国石油大学(北京) 安全与海洋工程学院北京 102249

2.油气生产安全与应急技术应急管理部重点实验室北京 102249

3.国家市场监督管理总局重点实验室(油气生产装备质量检测与健康诊断) 北京 102249

4.中国石油国际勘探开发有限公司北京 102100

An Integrated Corrosion Rate Prediction Model Based on Global and Local Error Fusion: A Robust Optimization Strategy

ZHENG Wenpei¹^,²^,³, LIU Yingzheng^,¹^,²^,³, ZHANG Yaru¹^,²^,³, ZHOU Taotao¹^,²^,³, LI Xingtao⁴, YU Shengyang⁴, JIANG Lumeng⁴

1.College of Safety and Ocean Engineering, China University of Petroleum (Beijing), Beijing 102249, China

2.Key Laboratory of Oil and Gas Safety and Emergency Technology, Ministry of Emergency Management, Beijing 102249, China

3.Key Laboratory of Oil and Gas Production Equipment Quality Inspection and Health Diagnosis, State Administration for Market Regulation, Beijing 102249, China

4.China National Oil and Gas Exploration and Development Corporation, Beijing 102100, China

通讯作者: 刘迎正，E-mail：liuyingzheng2024@126.com，研究方向为油气管道腐蚀预测

收稿日期: 2024-08-02 修回日期: 2024-12-06

基金资助:

中国石油天然气集团有限公司-中国石油大学(北京)战略合作科技专项：“一带一路”海外长输管道完整性关键技术研究与应用.  ZLZX2020-05
国家自然科学基金青年科学基金项目.  72301294
中国石油大学(北京)科研启动基金.  2462023BJRC016

Corresponding authors: LIU Yingzheng, E-mail:liuyingzheng2024@126.com

Received: 2024-08-02 Revised: 2024-12-06

Fund supported:

Strategic Cooperation Technology Projects of CNPC (China National Petroleum Corporation) and CUPB (China University of Petroleum, Beijing): Research and Application of Key Technologies for the Integrity of Overseas Long-distance Pipelines in the 'Belt and Road' Initiative.  ZLZX2020-05
National Natural Science Foundation of China.  72301294
Program for Youth Talents by the China University of Petroleum-Beijing.  2462023BJRC016

作者简介 About authors

郑文培，男，1981年生，博士，副教授

摘要

油气管道腐蚀速率的准确预测对维护管道安全至关重要，腐蚀速率预测模型的多样性和选择难度给实际应用带来了挑战。本文旨在改进传统的线性集成策略，首先综合全局与局部误差，提出了综合误差评价指标，并据此发展了一种新的线性集成策略，经5个标准测试函数的严格测试，证实了其广泛的适用性和优越性；将此策略应用于管道腐蚀速率预测，融合Fick定律(Fick's law algorithm，FLA)优化的BP神经网络(Backpropagation neural network)、克里金(Kriging)代理模型和极限学习机(Extreme learning machine，ELM)模型，成功构建了一个高效的集成预测模型。结果表明，与单一模型和传统集成模型相比，新策略在预测精度和稳定性上表现更优，当局部误差调节因子设定为0.5时，集成模型达到最佳性能；3个模型集成之后对比单个模型预测效果良好，预测效果有显著提升。该研究对于管道系统的可靠性评估和维护决策具有重要的工程应用价值。

关键词： 综合误差 ; 线性集成 ; 管道腐蚀 ; 速率预测

Abstract

Accurate prediction of the corrosion rate of oil and gas pipelines is crucial for maintaining pipeline safety, and the diversity and difficulty of choosing corrosion rate prediction models have brought challenges to practical applications. Herein, to improve the traditional linear integration strategy, firstly the global error and local error are synthesized and a comprehensive error evaluation index is postulated, then a novel linear integration strategy is established accordingly, its wide applicability and superiority are confirmed by rigorous testing with five standard test functions. By applying this strategy to the prediction of pipeline corrosion rate, an efficient integrated prediction model was successfully constructed via combining the FLA-optimized BP neural network, Kriging and ELM model. The results show that the new strategy performs better in terms of prediction accuracy and stability compared with the single model and the traditional integrated model, while the integrated model reaches the best performance when the local error adjustment factor is set to 0.5; In case the combination of the three models is adopted for prediction, it can produce better results rather than any single model, therefore the prediction effect is significantly improved. This study has important engineering application value for the reliability assessment and maintenance decision of pipeline systems.

Keywords： aggregate error ; linear integrated ; corrosion of pipeline ; rate prediction

PDF (1917KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

郑文培, 刘迎正, 张娅茹, 周涛涛, 李兴涛, 禹胜阳, 蒋璐朦. 基于全局与局部误差融合的集成腐蚀速率预测模型：一种稳健优化策略. 中国腐蚀与防护学报[J], 2025, 45(2): 523-532 DOI:10.11902/1005.4537.2024.242

ZHENG Wenpei, LIU Yingzheng, ZHANG Yaru, ZHOU Taotao, LI Xingtao, YU Shengyang, JIANG Lumeng. An Integrated Corrosion Rate Prediction Model Based on Global and Local Error Fusion: A Robust Optimization Strategy. Journal of Chinese Society for Corrosion and Protection[J], 2025, 45(2): 523-532 DOI:10.11902/1005.4537.2024.242

管道作为原油和天然气的主要运输方式，其安全性有着更高的标准和要求^[1]。而管道腐蚀是造成管道损伤的主要方式^[2]，其中CO₂腐蚀对管道的影响尤为显著^[3]。因此准确预测管道腐蚀速率对于管道的安全性有着十分重要的意义^[4]。

国内外学者针对管道腐蚀速率预测有了相关的研究。根据模型特点可分为物理模型和数据驱动模型,物理模型又可分为经验模型、半经验模型和机理模型。经验模型的代表是Norsok M-506模型^[5]，主要是依靠实验数据和现场数据拟合，适应性较差，难以广泛应用；半经验模型是考虑到腐蚀动力学和相关实验现场数据的模型，代表性的是DeWaard和Milliams^[6]于1975年提出的模型，预测结果较为保守；机理模型代表性的就是Nesic模型^[7]，尽管考虑了钢材表面电化学反应等因素，理论上具有一定优势，但由于相关模型参数难以从实验数据中获取，且影响管道腐蚀的因素及其相互作用机制十分复杂^[8]，导致其预测精度和适用性受到限制。

人工智能的快速发展使得相关学者渐渐热衷于机器学习算法的使用。机器学习算法对比传统物理模型有着“适应性”“处理大数据”“快速部署和实验”等优点^[9]。在管道腐蚀预测领域有着良好的应用。主要的方法如神经网络、支持向量机、灰色网络、深度学习等^[10~13]。周逸轩等^[14]利用核主成分分析法(Kernel principal component analysis，KPCA)进行腐蚀特征选择，利用遗传算法(Genetic algorithm，GA)进行BP神经网络的相关参数的优化，建立了KPCA-GA-BP模型，在集输管道内腐蚀预测取得了较好的准确性。张新生和常潆戈^[15]建立基于因子分析(Factor analysis，FA)和天牛须搜索算法(Beetle antennae search，BAS)的极限学习机(Extreme learning machine，ELM)腐蚀速率预测模型，以实海挂片试验为例，通过建模仿真评价模型的预测性能，并与其他模型进行对比分析，决定系数高达0.9949。郑度奎等^[16]为提升油田集输管道的CO₂腐蚀预测的准确性，使用了人工鱼群算法(AFSA)优化了广义回归神经网络(GRNN)模型，提升了模型的预测精度和收敛速度。Lee等^[17]利用支持向量机(Support vector machine，SVM)分类方法进行了油气管道腐蚀故障智能预测，实现了油气管道状态的连续监测。Bastian等^[18]使用卷积神经网络(Convolutional neural network，CNN)对管道腐蚀图像进行分类，准确率较高，但该方法更多的针对图像数据进行的预测分析。针对于管道腐蚀预测领域，虽然目前提出了众多的机器学习模型，并且也取得了较好的效果。但是不同模型在精度和稳定性方面的表现各有差异，在缺少先验知识的情况下，使得模型的选择变得困难。

集成学习模型通过整合多个独立的基本模型，利用他们各自的优势进行综合学习和预测。通过多模型投票或加权平均的方式，提高了整体预测的准确性和稳定性。常用的集成学习算法例如自适应增强算法(AdaBoost)、梯度提升决策树(Gradient boosting decision trees，GBDT)、极限梯度提升算法(XGBoost)等^[19]。张雪等^[20]利用集成学习预测了锈蚀RC梁抗弯承载力，对比了5种集成学习算法的预测性能，结果表明集成学习算法具有良好的预测性能。蔡宝泉^[21]利用集成学习算法预测海洋管道腐蚀，在3个单一的集成学习算法基础之上建立了堆叠(Stacking)融合模型，展现了Stacking融合模型的预测精度和稳定性。相关学者更多的是利用的是集成学习算法(如AdaBoost、Gradient boosting等)直接进行的相关模型测试，这类模型较为复杂，在数据量不足时会出现过渡拟合模型的情况^[22]。而手动融合模型有着灵活性高、适用性广泛和较强的解释性等优势，对于未知不同模型的探索有着重要意义。

模型的选择对于集成学习十分重要。预测模型除了前边提到过的机器学习模型之外还有插值模型等。将两种模型的结合是一个值得尝试的思路。机器学习代表性的就是BP神经网络^[23]，而引入优化算法可以使得神经网络寻找到更优化的参数。张娅茹^[24]研究表明，FLA优化的神经网络效果良好。此外，ELM在小数据量快速回归方面有着优异的表现。吕林林等^[25]利用ELM算法预测管道内腐蚀速率，确定了最优的ELM模型结构。对比其他插值模型中Kriging模型有着适应非均匀数据分布、强大的自适应能力等优点。周逸轩等^[26]利用拉丁超立方抽样(LHS)优化了克里金模型用于预测集输管道内腐蚀速率，模型误差相对较小。

算法优化的BP神经网络模型在捕捉非线性关系方面具有显著优势^[27]；Kriging模型则在处理空间相关性^[28]方面表现出色；而ELM模型以其快速的计算速度和优越的泛化能力而受到青睐^[29]。将这3种模型结合起来，充分发挥各自的特长，并融合到集成模型中，是一种创新性的尝试。

预测模型的评价指标可以反映模型的应用效果，而不同的评价指标关注的重心有所不同。在机器学习预测模型领域评价指标可分为全局误差和局部误差。全局误差侧重于整个数据集上模型预测与实际值之间的差异。局部误差则能反映数据集的特定区域或特定条件下的表现^[30]。目前大多数的预测模型采用的评价指标都是全局误差^[31~33]。局部误差使用较少，滕起^[34]利用局部误差和卷积神经网络结合，用于人体识别任务，较传统的全局误差，局部误差可逐层地训练卷积神经网络，性能有所提升。

本文提出了一种基于综合误差评价指标的集成模型。首先考虑了全局误差和局部误差，提出了基于综合误差的稳健集成预测策略，并采取5个测试函数对其优化性能进行验证，然后以FLA优化的BP神经网络算法、Kriging代理模型和ELM模型为算例，证明了集成模型的优越性，这对于管道的可靠性评估，剩余寿命评价以及管道的维修等，具有一定的工程意义。

1 基础理论模型

1.1 Kriging模型

Kriging模型由南非矿业工程师Krige提出^[35]，逐渐发展为统计学中的一种插值法。Kriging模型是利用样本和函数的相关关系，对被测样本的函数进行预测；换句话说，Kriging假设一个位置的变量值与附近位置的值相关，并利用这种关系对新的位置进行预测。

Kriging模型由线性回归和非参数部分组成，二者相互协作以实现模型的预测和插值^[36]，具体数学形式如下：

g (x) = F (β, x) + Z (x) = f^{T} (x) β + Z (x)

(1)

其中，F(β, x)为线性回归部分；f(x) = [f₁(x), f₂(x), …, f_n (x)]为回归函数；β为回归系数；Z(x)为服从标准正态分布的随机误差，其协方差为：

C o v (Z (x_{i}), Z (x_{j})) = δ^{2} R_{θ} (x_{i}, x_{j})

(2)

其中，θ为相关函数；R_θ (x_i, x_j )为样本点的相关函数^[37]，可表示为：

R_{θ} (x_{i}, x_{j}) = e x p (- \sum_{i = 1}^{m} θ_{k} (x_{i}^{k} - x_{j}^{k})^{2})

(3)

其中，m为输入样本空间的维数；k为θ、x_i 、x_j 的第k个分量。

设M个输入样本点为x = [x₁, x₂, …, x_m ]^T，它所对应的响应值为G = [g₁, g₂, …, g_M ]^T。设待测点为X₀，其响应值可表示为：

\hat{g} = C^{T} G

(4)

此时，Kriging模型的预测误差为

\hat{g} - g = C^{T} G - g = C^{T} Z - Z + {(F^{T} C - f)}^{T} β

(5)

其中，F由f(x)组成，为尽可能使建立的模型预测的偏差小，需要确保预测的误差均值为0，方差也要尽量小，即:

F^{T} C - f = 0

(6)

φ (x_{0}) = δ^{2} (1 + C^{T} R C - 2 C^{T} r)

(7)

其中：R为不同输入变量相关函数组成的矩阵；r为待测点与输入变量之间的相关矩阵；

采用Lagrange乘子法，联立上面的两个式子，求出φ(x₀)的最小值；

当 $\tilde{λ}$ = -λ/2δ²时，Kriging模型的预测值可表示：

\hat{g} = {(r - F \tilde{λ})}^{T} R^{- 1} G = f^{T} \hat{β} + r^{T} R^{- 1} (Y - F \hat{β})

(8)

其中， $\hat{β}$ 为回归系数β的广义最小二乘解。

待测点预测值的均方差为：

{\hat{δ}}_{\hat{g}}^{2} (x_{0}) = δ^{2} (1 + u^{T} {(F^{T} R^{- 1} F)}^{- 1} u - r^{T} R^{- 1} r)

(9)

其中，u = F^TR^-1 - f。

1.2 极限学习机

ELM是一种前馈神经网络，它通过随机初始化输入权重和偏置参数，避免了传统神经网络训练中的过拟合、局部最优和收敛速度缓慢的问题。

对于任意的N个不同样本(x_j, y_j )，其中x_j = (x₁_j, x₂_j, …, x_nj )^T∈Rⁿ，y_j = (y₁_j, y₂_j, …, y_mj )^T∈R^m，有两条重要的定理：(1) 在隐藏层节点数等于样本数时，输入权重和偏置的选择方式对模型性能影响不大。当隐藏层输出矩阵H是满秩且可逆时，存在唯一的输出权重||Hβ- $\hat{Y}$ || = 0。(2) 隐含层神经元个数小于训练样本数时，给定任意小的误差ε > 0，总存在一组输入权重和偏置，使得||Hβ- $\hat{Y}$ || < ε，此时可以使用最小二乘法求出权重β。

\hat{β} = H^{+} \hat{Y}

(10)

其中，H⁺ 为隐含层输出矩阵H的Moore-Penrose广义逆矩阵。 $\hat{Y}$ 为期望输出。

在上述原理的基础上，ELM算法的实现过程为：

(1) 确定激活函数g(x)和隐含层神经元个数；

(2) 随机产生输入权值和隐含层权值；

(3) 求解隐含层输出矩阵H；

(ω_{1} \dots ω_{l}, b_{1} \dots b_{l}, x_{1} \dots x_{N}) = [\begin{array}{l} g (ω_{1} x_{1} + b_{1}) \dots g (ω_{1} x_{1} + b_{l}) \\ ⋮ ⋮ ⋮ \\ g (ω_{1} x_{N} + b_{1}) \dots g (ω_{1} x_{N} + b_{l}) \end{array}]

(11)

其中，为第i个隐含层神经元与输出层神经元的连接权值；b_i 为第i个隐含层神经元的阈值；x_i 为输入样本；g(x)为隐含层激励函数。

(4) 求解网络输出权值β。

1.3 传统线性集成理论

传统线性集成模型的思想是通过加权的形式充分利用不同独立元模型的预测能力。构建传统线性集成模型的一般形式可以定义为：

{\hat{y}}_{e} (x) = \sum_{i = 1}^{N} ω_{i} {\hat{y}}_{i} (x)

(12)

其中， $\sum_{i = 1}^{N} ω$ _i = 1， ${\hat{y}}_{e}$ 为集成模型的预测响应，N是元模型的数量，ω_i 、y_i 分别为第i个元模型的权重系数和预测响应值。

构建集成模型有两个关键因素。第一个因素是元模型的选择，第二个因素是计算每个元模型对应的权重系数。一般来说，预测精度越高，相应元模型的权重系数越大。

传统的权重系数计算方法如下：

ω_{i} = \frac{\frac{1}{V_{i}}}{\sum_{j = 1}^{N} V_{j}}, \sum_{i = 1}^{N} ω_{i} = 1

(13)

其中，V_i 是第i个元模型的预测方差。

2 基于综合误差的稳健集成模型

2.1 全局和局部误差评估

常用的全局误差评价指标有GMSE^[38]，GMSE是基于留一交叉验证计算全局误差，计算成本高，当数据量较大时会严重影响集成模型的计算效率。于是，为了快速精准的评价全局误差，本文基于全局准确度指标(R²)建立了一种新的全局误差值指标。R²的范围为0~1，R² 的大小彰显了模型的拟合程度，越接近1表示拟合程度越好，越小则相反，表达式如式(14)

R^{2} = 1 - \frac{{\sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - {\bar{y}}_{i})}^{2}}

(14)

其中，n为样本个数。

基于R²这一概念，构建一种新的全局误差评价指标即1-R²，令G = 1-R²。

G = \frac{{\sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})}^{2}}{{\sum_{i = 1}^{n} (y_{i} - {\bar{y}}_{i})}^{2}}

(15)

局部误差反映了单次计算中的误差大小，它是评估数值方法精度的一个重要指标。与其他局部误差评价指标相比，最大绝对误差(Maximum absolute error，M_ae)较离群值敏感性较弱，更适合作为局部误差的评价指标。其计算公式如下：

M_{a e} = M a x |y_{i} - {\hat{y}}_{i}|

(16)

其中，y_i 为真实响应， ${\hat{y}}_{i}$ 为预测响应。

2.2 基于综合误差的线性集成权重计算

在集成模型中，通过融合各自具有不同优势和局限的多个模型，可以增强预测的准确性和鲁棒性。本文提出了一种基于全局误差G和局部误差M_ae的综合评价指标，用以优化模型权重分配，从而提高集成模型的整体预测性能，具体如式(17)：

M_{i} = G_{i} + α M_{a e, i}, 0 < α < 1

(17)

其中，α为局部误差M_ae的调节因子。

为保持模型整体精度，本研究将全局误差调节因子设为1。局部误差调节因子α设为一个0到1之间的值，以平衡特定区域的预测精度。若该值过高，则可能过度强调局部误差；若为0，则忽略局部误差。后续将通过测试确定其最优取值。

于是，基于综合误差指标，各模型权重ω_i 可按公式进行计算。

ω_{i} = \frac{\frac{1}{M_{i}}}{\sum_{j = 1}^{N} \frac{1}{M_{i}}} = (i = 1, \dots, N), \sum_{i = 1}^{N} ω_{i} = 1

(18)

其中，N为模型的个数，M_i 为综合误差评价指标。

2.3 性能验证

根据式(18)可得，综合误差越大的模型，对其的权重选择越小。α值的选取是一个关键，本节将利用标准测试函数，并针对测试函数采用随机抽样的方法生成样本构建数据集，对其进行性能验证。从标准测试函数库中选择了5个具有代表性的基准函数，它们可以代表低维、高维、低阶和高阶的情况。具体的表达式如表1所示。

表1 基准功能

Table 1 Benchmark functions

Sample	Displayed formula
1	y = x₁exp (-(x $_{1}^{2}$ + x $_{2}^{2}$ )), x_i ∈[-2, 2]
2	y = 2x $_{1}^{2}$ - 1.05x $_{1}^{4}$ + $\frac{x_{1}^{6}}{6}$ + x₁x₂ + x $_{2}^{2}$ , x_i ∈[-5, 5]
3	y = ${(x_{2} - \frac{5.1 x_{1}^{2}}{4 π^{2}} + \frac{5 x_{1}}{π} - 6)}^{2}$ + 10 $(1 - \frac{1}{8 π})$ cosx₁ + 10, x₁∈[5, 10], x₂∈[0, 15]
4	y = 10sin[2(x₁ - 0.6 $π$ )] + x₂ + x₃ + x₄ + x₁x₂ + x₃x₄ + x $_{1}^{3}$ + x $_{4}^{3}$ , x_i ∈[0, 1]
5	y = $\sum_{i = 1}^{7} [\frac{3}{10} + s i n (\frac{16}{15} x_{i} - 1) + s i n^{2} (\frac{16}{15} x_{i} - 1)]$ , x_i ∈[-1, 1]

新窗口打开| 下载CSV

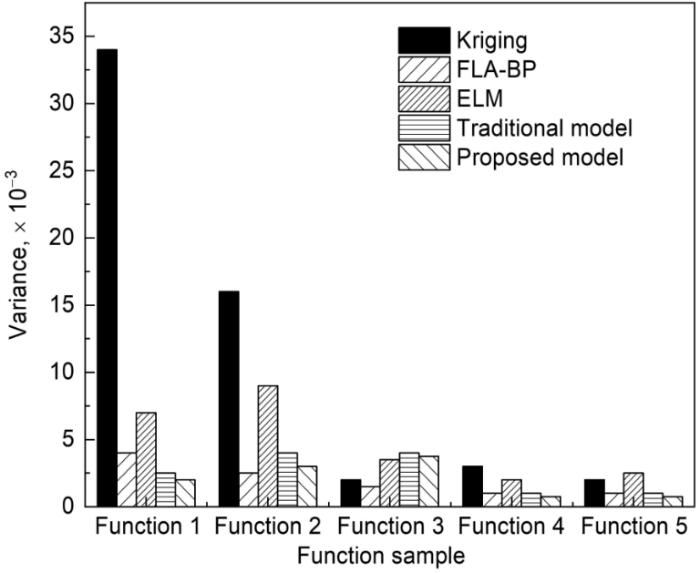
对于这5个基准测试，建立了3个元模型(Kriging、ELM和FLA-BP)和5个对应于不同α (0，0.2，0.4，0.5，0.6，0.8)值的集成模型。利用方差和平均相对误差评价各模型的预测性能，如表2所示。

表2 集成模型预测的比较

Table 2 Comparison of integrated model predictions

Sample	MEAE	Kriging	FLA-BP	ELM	α = 0.2	α = 0.4	α = 0.5	α = 0.6	α = 0.8
	Average	1.0012	0.8812	1.2143	0.7709	0.7703	0.7607	0.7741	0.9021
1	Variance, × 10^-3	34.372	4.4142	6.9803	2.9341	2.8674	2.6806	2.9877	3.0785
	Average	1.1075	0.7706	2.2398	0.7821	0.7510	0.7442	0.8186	0.8724
2	Variance, × 10^-3	15.987	3.1354	10.082	3.2458	3.0584	3.2463	4.2351	4.5526
	Average	0.9653	0.7533	1.0436	0.7709	0.7703	0.7607	0.7741	0.9021
3	Variance, × 10^-3	1.0359	0.8635	3.6522	4.2536	4.0863	3.9655	3.9763	4.3691
	Average	0.0203	0.0031	0.3136	0.0029	0.0028	0.0025	0.0065	0.0098
4	Variance, × 10^-3	2.6354	0.6952	1.3655	0.5563	0.5536	0.4695	0.6353	0.7466
	Average	0.0012	0.0005	0.0102	0.0009	0.0009	0.0007	0.0008	0.0010
5	Variance, × 10^-3	1.3653	0.6654	1.9633	0.7633	0.7464	0.6667	0.9616	1.0153

新窗口打开| 下载CSV

从表2、图1和2中可以看出，与传统线性集成模型相比，在α取值的5种情况下，大部分情况下本文所提出的集成模型的精度高于传统线性模型。这些结果表明，本文所提出的集成模型具有在预测精度方面优于传统线性集成模型的潜力。本节提出的局部误差和全局误差相结合的算法，在一定程度上提高了集成模型的预测精度。从表2中可以看出，α的值为0.5时集成模型的方差最小，因此局部误差调节因子的最优取值为0.5。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 集成模型方差对比图

Fig.1 Comparison chart of variances of five integrated models

图2

新窗口打开| 下载原图ZIP| 生成PPT

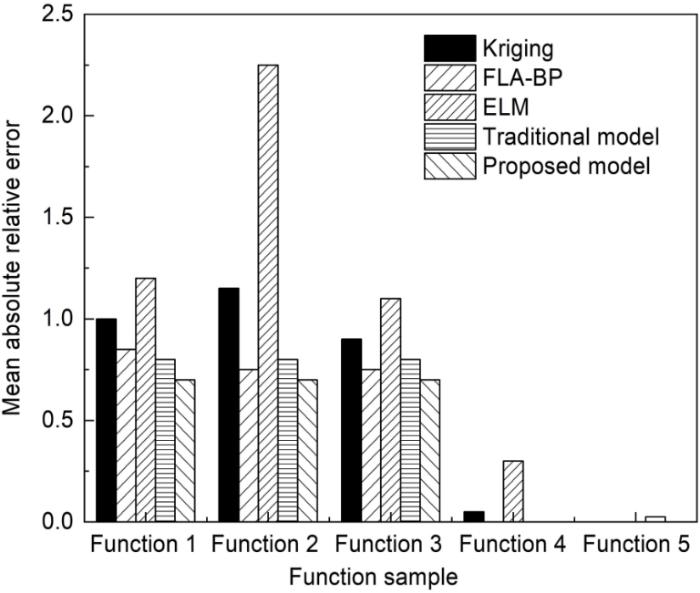
图2 集成模型平均相对误差对比图

Fig.2 Comparison chart of mean relative errors of five integrated models

2.4 融合FLA-BP管道腐蚀腐蚀速率预测模型建立

2.4.1 数据预处理

基于上文提出的集成模型策略，将主流的预测模型集成，构建了一个更加稳健精准的管道腐蚀预测模型。先导入从文献[39,40]中找到的数据样本案例，如表3所示。X₁~X₈分别是：运行温度(℃)、pH、O含量(mg·kg^-1)、CO₂含量(%)、S含量(mg·kg^-1)、N含量(mg·kg^-1)、流速(m·s^-1)。V_corr为腐蚀速率(mm/a)。此数据为东北某石油工艺管道在不同条件下的腐蚀速率及其影响因素。为了消除量纲不一致的问题，会对数据进行标准化处理，本文采用的是Min-Max标准化，进行标准化处理之后，数据会被放到[-1, 1]的区间内，标准化部分数据如表4所示。

表3 管道腐蚀监测部分数据

Table 3 Part of pipeline corrosion monitoring data

Sample	X1	X2	X3	X4	X5	X6	X7	X8	V_corr
1	109.03	6.5100	0.0717	1.1824	35.887	0.7636	0.9033	0.1050	0.1898
2	115.12	6.3578	0.0370	1.6696	37.932	0.7561	0.8283	0.1240	0.1497
3	115.05	6.2169	0.0838	3.2597	37.306	0.7701	0.8673	0.1102	0.1525
4	110.56	6.3860	0.1065	1.4988	36.520	0.7601	0.8581	0.1127	0.1746
5	110.66	6.5301	0.0535	2.5883	37.896	0.7622	0.8601	0.1232	0.1641
6	114.09	6.5905	0.0565	4.8084	37.097	0.7712	0.8809	0.1149	0.1528
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
150	113.18	6.3849	0.0608	4.3186	37.839	0.7645	0.8497	0.1150	0.1485

新窗口打开| 下载CSV

表4 标准化后部分数据

Table 4 Normalized partial data

Sample	X1	X2	X3	X4	X5	X6	X7	X8	V_corr
1	0.9621	0.8157	-0.5651	-0.2026	0.1234	0.6291	-0.1607	0.1975	1.0000
2	0.6001	0.1622	0.3896	-0.4472	0.1574	0.0654	0.9870	0.0096	0.5044
3	0.8462	0.3619	-0.0432	0.0965	-0.1003	0.5975	0.2789	-0.0343	0.5412
4	-0.5925	0.4254	-0.2301	-0.4480	0.2983	-0.8951	-0.3238	0.1194	0.8190
5	0.3094	-0.1121	-0.3212	-0.0539	0.3443	-0.6101	-0.0699	-0.6429	0.6901
6	-0.1407	-0.2053	-0.3387	-0.1544	0.0101	-0.9614	0.2104	-0.4095	0.6533
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
150	0.2237	0.4388	-0.5234	0.0295	0.0112	0.2865	-0.2689	0.6539	0.5467

新窗口打开| 下载CSV

2.4.2 模型参数调整策略

本文使用的BP神经网络训练算法为Bayes正则化算法，学习率设置为0.1，训练误差为10^-3，训练次数设置为100。隐含层节点数按照l < $\sqrt[]{n + m}$ + a确定，l、n、m分别为隐含层、输入层和输出层节点数，a为0~10之间的常数，根据枚举法于MATLAB中反复确定尝试和训练，最终确定为10。引入FLA算法之后，设置适应度函数最小化预测误差，获得神经网络最优的权值和阈值。

Kriging模型的参数，主要是协方差函数的参数，采用了最大似然估计方法进行估计。通过最大化数据的似然函数，可得到最佳的协方差参数，确保了模型对空间相关性的准确捕捉，在MATLAB的Fitrgp函数选项可实现参数的自动优化。

对于ELM模型，采用了随机特征选择的方法来确定隐藏层节点的权重和偏置。输入权重和偏置的随机初始化，结合随机的隐藏层节点数量，使得ELM模型在训练过程中具有较高的灵活性和泛化能力。

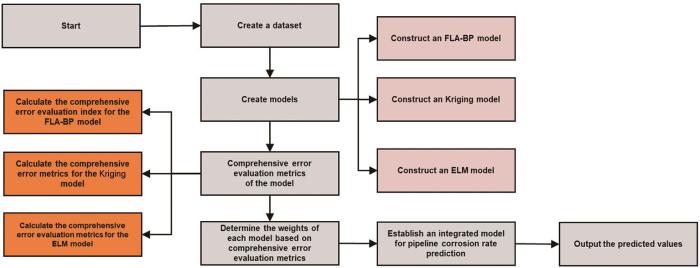
2.4.3 集成模型构建

用样本数据建立FLA-BP、Kriging、ELM模型，然后采用式(17)得到各模型的综合误差分别为M₁、M₂、M₃，基于各模型综合误差指标计算权重系数，构建集成模型，验证集成模型的预测精度和鲁棒性。框架图如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 模型流程图

Fig.3 Flowchart of model construction

3 融合FLA-BP的管道腐蚀速率稳健预测模型对比验证

3.1 基于单一模型和集成模型的管道腐蚀速率预测

基于选择的3个主流的模型分别进行了单独的管道腐蚀速率预测，并得到了相应的结果。这些单一模型的预测结果将被用作比较基准，以评估集成模型的性能和优越性。通过单独使用这些模型进行预测，可以更好地了解它们在管道腐蚀速率预测问题上的表现和特点，并为后续的集成模型设计和优化提供重要参考。单一预测模型和集成预测模型的均方误差如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 3种模型及其集合误差对比

Fig.4 Comparison of errors of three models and their set

深入分析3个模型的预测结果，可以发现，Kriging模型的误差波动幅度最大，其误差波动范围约为-0.09~0.07。这种较大的误差波动可能是由于Kriging模型在拟合复杂非线性系统时的局限性所导致的。相比之下，FLA-BP模型和ELM模型的误差波动范围较小，没有出现过大的误差波动点，预测结果相对平稳可靠。在这几个单模型中，FLA-BP模型的预测效果表现最佳。其均方误差和平均绝对误差分别为1.1893 × 10^-6和0.0054。这种出色的表现可能是由于FLA-BP模型在处理非线性系统时具有更强的适应性和泛化能力。

通过图4可明显观察到ELM和Kriging的误差波动较大，而三模型集成后的模型在大多数点上的误差要比单独使用FLA-BP的预测效果更小，通过表5可以看到，其均方误差和平均相对误差分别为7.1065 × 10^-7和0.0047，相比于单独的模型预测误差较小。因此，可以得出结论：三模型集成后的预测效果优于单一模型。

表5 3种模型以及它们的集合预测效果对比

Table 5 Comparison of prediction effects of three models and their set

Model	Mean squared error	Mean absolute error
Kriging	1.7451 × 10^-5	0.0198
ELM	1.9938 × 10^-6	0.0079
FLA-BP	1.1893 × 10^-6	0.0054
FLA-BP + Kriging + ELM	7.1065 × 10^-7	0.0047

新窗口打开| 下载CSV

3.2 模型数量对于集成模型预测性能敏感性分析

为了更全面地探究模型数量对于集成模型预测效果的影响，对3个不同的元模型进行排列组合，分别为ELM + Kriging、ELM + FLA-BP以及Kriging + FLA-BP。这3种元模型在集成模型中各自具有不同的特点，其组合可以更好地反映模型之间的协同作用和互补性。经过相关检验，相关模型组合及其误差如表6所示。

表6 不同集成模型预测效果对比

Table 6 Comparison of prediction effects of set models based on two or three of Kriging, ELM and FLA-BP models

Model	Mean squared error	Mean absolute error
FLA-BP + Kriging	9.7434 × 10^-7	0.0052
FLA-BP + ELM	7.9774 × 10^-7	0.0048
ELM + Kriging	1.7606 × 10^-6	0.0078

新窗口打开| 下载CSV

通过表5和6的数据可以得知，在单一模型和不同模型的组合中，依旧是三模型的集成效果最为显著，其平均绝对误差和均方误差分别为0.0047和7.1065 × 10^-7,由此可知三模型的集成预测性能最好。因此，三模型集成策略不仅在理论上具有优势，而且在实际应用中也显示出了卓越的性能，为管道腐蚀速率的准确预测提供了一种有效的解决方案。这种集成方法的优越性可能源于各模型之间的互补性，其中每个模型都可能捕捉到数据中的不同特征，而集成方法则有效地结合了这些特征，提高了整体的预测性能。

4 结论

(1) 本文提出的新线性集成策略，通过在5个标准测试函数上的测试，证明了其在预测精度和稳定性上的优越性。与单一模型和传统集成模型相比，所提出的集成模型在平均相对误差的均值和方差上均表现更佳。特别地，当局部误差调节因子为0.5时，集成模型的性能达到最优，这为模型的参数调整提供了重要指导。

(2) 将该集成策略应用于管道腐蚀速率预测领域，通过集成Kriging模型、ELM模型和FLA-BP模型，建立了基于综合误差评价指标的管道腐蚀速率预测模型。预测结果与单模型对比表明，集成模型在预测效果上具有显著优势。此外，模型数量和种类对预测效果有显著影响，建议在追求高精度预测时，采用3种模型的集成策略。

本文提出的线性集成策略展示了如何通过综合考虑全局误差和局部误差，来优化模型的预测性能，此框架这未来可以将其应用于不同的机器学习算法，以进一步提高预测的准确性和效率。通过研究不同集成方法的适用性和优化策略，未来将有望在更多实际应用中验证和拓展该方法，从而推动管道腐蚀预测领域的技术进步。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Wang

, Lu

J W

, Zhou

L L

, et al.

Corrosion analysis and protective measures of pressure piping of atmospheric and vacuum unit

[J]. Sichuan Chem. Ind., 2022, 25(1): 26