基于PDM的304不锈钢钝化膜生长动力学研究

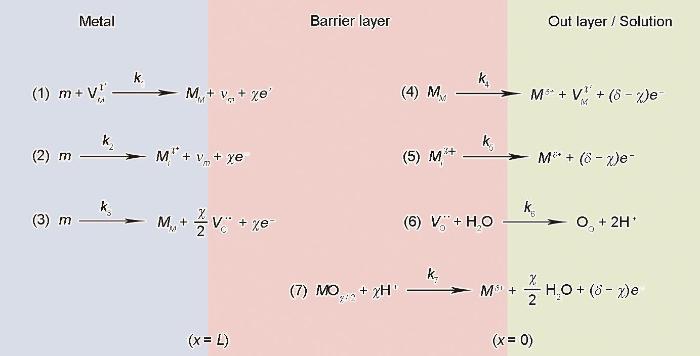
图1 PDM中假设的表示点缺陷产生和湮灭的界面反应

Fig.1 Interfacial defect generation/annihilation reactions happened hypothetically in the growth of anodic barrier oxide films according to PDM. For the symbols, m is metal atom, $V_{M}^{χ'}$ is cation vacancy on the metal sublattice of the barrier layer, $M_{i}^{χ +}$ is interstitial cation, $M_{M}$ is metal cation on the metal sublattice of barrier layer, $V_{O}^{∙ ∙}$ is oxygen vacancy on the oxygen sublattice of barrier layer. $O_{O}$ is oxygen anion on the oxygen sublattice of barrier layer, $M^{δ +}$ is metal cation in solution

表1 界面反应的速率常数表达式 $k_{i} = k_{i}^{0} e^{a_{i} V} e^{b_{i} L} e^{c_{i} p H}$ 中的系数

Table 1 Various coefficients in the rate constants of the interfacial reactions, i.e. $k_{i} = k_{i}^{0} e^{a_{i} V} e^{b_{i} L} e^{c_{i} p H}$

Reaction	$a_{i} / V^{- 1}$	$b_{i} / c m^{- 1}$	c_i	Units of $k_{i}^{0}$
(1) $m + V_{M}^{χ'} \overset{k_{1}}{\to} M_{M} + ν_{m} + χ e'$	$α_{1} (1 - α) χ γ$	$- α_{1} χ K$	-α₁βχγ	$\frac{1}{S}$
(2) $m \overset{k_{2}}{\to} M_{i}^{χ +} + ν_{m} + χ e'$	$α_{2} (1 - α) χ γ$	$- α_{2} χ K$	-α₂βχγ	$\frac{m o l}{c m^{2} \cdot s}$
(3) $m \overset{k_{3}}{\to} M_{M} + \frac{χ}{2} V_{O}^{∙ ∙} + χ e'$	$α_{3} (1 - α) χ γ$	$- α_{3} χ K$	-α₃βχγ	$\frac{m o l}{c m^{2} \cdot s}$
(4) $M_{M} \overset{k_{4}}{\to} M^{δ +} + (δ - χ) e'$	$α_{4} α δ γ$	-	α₄βδγ	$\frac{m o l}{c m^{2} \cdot s}$
(5) $M_{i}^{χ +} \overset{k_{5}}{\to} M^{δ +} + (δ - χ) e'$	$α_{5} α δ γ$	-	α₅βδγ	$\frac{c m}{s}$
(6) $V_{O}^{∙ ∙} + H_{2} O \overset{k_{6}}{\to} O_{O} + 2 H^{+}$	$2 α_{6} α γ$	-	α₆βδγ	$\frac{c m}{s}$
(7) $\begin{array}{l} M O_{χ / 2} + χ H^{+} \overset{k_{7}}{\to} M^{δ +} + \\ \frac{χ}{2} H_{2} O + (δ - χ) e' \end{array}$	$α_{7} α (δ - χ) γ$	-	α₇(δ-χ)βγ	$\frac{m o l}{c m^{2} \cdot s}$

L_{s s} = \frac{1}{ε} [1 - α - \frac{α α_{7}}{α_{3}} (\frac{δ}{χ} - 1)] V + \frac{1}{ε} \{\frac{2.303 n}{α_{3} χ γ} - β [\frac{α_{7}}{α_{3}} (\frac{δ}{χ} - 1) + 1]\} p H + \frac{1}{α_{3} χ K} l n (\frac{k_{3}^{0}}{k_{7}^{0}})

(1)

式中，ε是阻挡层内的电场强度，n是钝化膜/溶液界面的溶解反应中H⁺的动力学级数，α和β分别表示穿过钝化膜/溶液界面的电位降与V和pH的相关系数，V为外加电位。γ=F/RT，F、R和T分别代表Faraday常数、气体常数和温度。根据图1中的反应 (3) 和 (7)，钝化膜厚度 (L) 与时间 (t) 之间的关系如公式 (2) 所示：

\frac{d L}{d t} = Ω k_{3} - Ω k_{7} (\frac{C_{H^{+}}}{C_{H^{+}}^{0}})

(2)

式中，Ω是MO_χ/2的化学计量数， $C_{H^{+}}$ 、 $C_{H^{+}}^{0}$ 分别为溶液中氢离子浓度和标态氢离子浓度 ( $C_{H^{+}}^{0}$ =1 mol/L)。对于n型半导体，稳定的钝化电流密度可通过公式 (3) 表示：

I_{s s} = F [χ k_{2} + χ k_{3} + (δ - χ) k_{5} C_{i}^{0} + (δ - χ) k_{7}]

(3)

因此，电流密度与电位和钝化膜的厚度的关系可用公式 (4) 表示：

δ I = {(\frac{\partial I}{\partial V})}_{L} δ V + {(\frac{\partial I}{\partial L})}_{V} δ L

(4)

在电化学阻抗谱中采用的是正弦变化的交流信号，因此δV=ΔVe ^jωt，δL=ΔLe ^jωt，那么Faraday导纳可表示为：

Y_{f} = \frac{δ I}{δ V} = I^{V} + I^{L} \frac{Δ L}{Δ V}

(5)

式中， $I^{V} = \partial I / \partial V$ ， $I^{L} = \partial I / \partial L$ ，其微分式可从公式 (3) 得到， $∆ L / ∆ V$ 可由公式 (6) 表示：

\frac{Δ L}{Δ V} = \frac{Φ_{3}}{1 + j ω τ_{3}}

(6)

上式中 $Φ_{3} = (\frac{a_{3}}{b_{3}}) - (\frac{k_{7}^{0}}{k_{3}^{0}}) (\frac{a_{7}}{b_{3}}) e^{(a_{7} - a_{3}) V + b_{3} L} C_{H^{+}}^{n}$ ， $τ_{3} = \frac{1}{Ω k_{3}^{0} b_{3} e^{a_{3} V - b_{3} L}}$ ，Faraday导纳最终可定义为

Y_{f} = I^{V} + I^{L} \frac{Φ_{3}}{1 + j ω τ_{3}}

(7)

这里没有考虑在钝化膜/溶液界面处能导致[H⁺]浓度变化的任何弛豫现象，因此需要采用缓冲溶液来保证稳定的pH值。模型的更多推导细节可以参考相关文献^[12,13]。图1中的反应2和反应3都是不可逆反应，因此不受金属/钝化膜界面处的氧空位和间隙离子浓度的影响。假设法拉第电阻不包含任何缺陷的弛豫，但实际上明显有扩散存在，因此添加Warburg阻抗来表示缺陷的扩散运动^[9]。

Z_{W} = σ ω^{- 1 / 2} - j σ ω^{- 1 / 2}

(8)

式中， $ω$ 是角频率， $σ$ 是Warburg系数，其可以表示为公式 (9)：

σ = D^{1 / 2} ε / 2^{1 / 2} (1 - α) I_{s s}

(9)

从而阻挡层内的缺陷扩散系数D可以表示为公式 (10)：

D = 2 σ^{2} {(1 - α)}^{2} I_{s s}^{2} / ε^{2}

(10)

需要注意的是阻挡层内缺陷的电子特征会影响点缺陷在其内的分布。阳离子空位是电子受主，当它为主要缺陷时阻挡层是p型半导体；而阳离子间隙或氧空位是电子施主，当它们是主要缺陷时，阻挡层是n型半导体。从电化学阻抗数据中获得的动力学参数能确认阻挡层内的缺陷浓度及其电子特征。

2.2 电化学测试与PDM分析

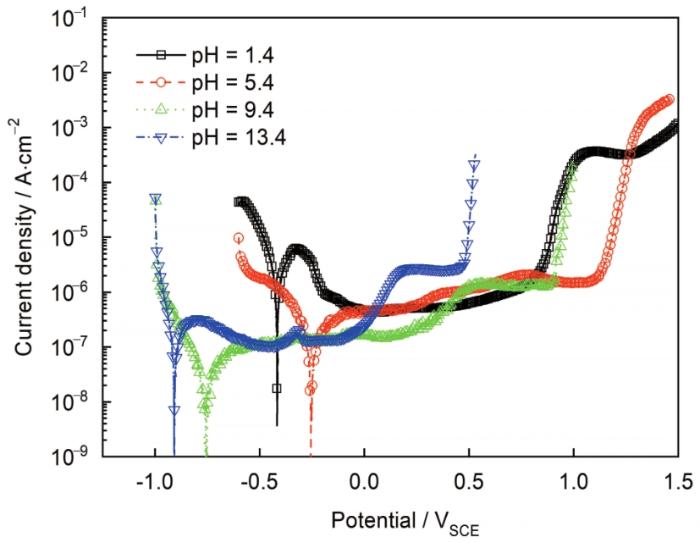
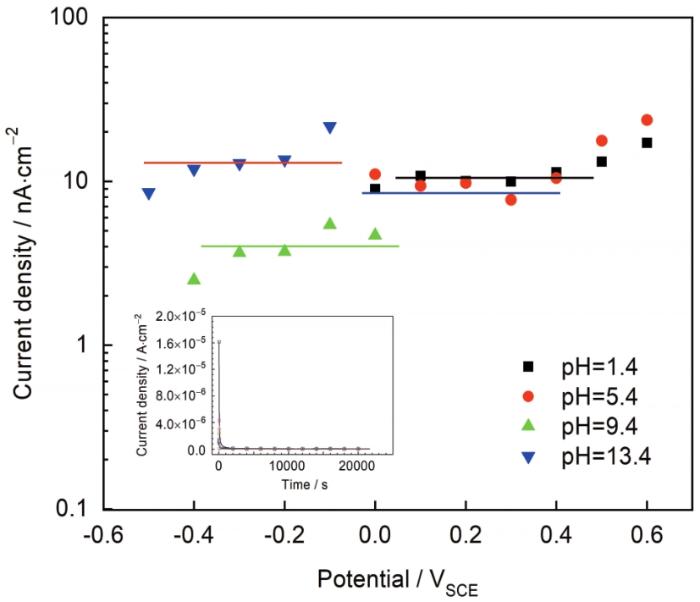
图2所示为304不锈钢在不同pH溶液中的动电位极化曲线。在酸性溶液中钝化区间为-0.2~0.8 V_SCE (pH=1.4) 和0~1.1 V_SCE (pH=5.4)，碱性溶液中的钝化区间为-0.6~0.8 V_SCE (pH=9.4) 和-0.8~0.5 V_SCE (pH=13.4)。随着溶液pH增加，钝化区域向电位负方向移动。在钝化区间选取几个电位，形成表面稳定膜并进行电化学阻抗测试。图3所示为304表面稳态钝化电流与所施加电压的关系。可以看出，施加电压不会对稳态电流数值产生影响，表明阻挡层内的主要缺陷是n型半导体，这通过之后的M-S测试也可以证明。图3中的小插图是6 h恒电位极化时电流密度随时间变化的关系图，在所施加电压下电流密度随时间变化保持恒定表明阻挡层的生长和溶解是同时进行的且达到平衡^[14]。

图2

图2 304不锈钢在不同溶液中的动电位极化曲线

Fig.2 Potentiodynamic polarization curves for Type 304 stain steel in the test solutions with different pH values

图3

图3 304不锈钢在不同溶液中的稳态 (恒电位极化) 电流密度与电位及电流随时间的曲线

Fig.3 Steady state (potentiostatic) current densities of 304 stainless steel in the test solutions with different pH values as a function of oxide formation potential. The inset shows the current vs. time curves

M-S测试可以用来分析半导体的电子特征，还可以定量的计算出半导体的缺陷密度等。p型和n型半导体中电荷容量可通过以下方程表示：

\frac{1}{C_{s c}^{2}} = \frac{- 2}{\hat{ε} ε_{0} e N_{A} A^{2}} (V - V_{F B} - \frac{k T}{e}) p - t y p e

(11)

\frac{1}{C_{s c}^{2}} = \frac{2}{\hat{ε} ε_{0} e N_{D} A^{2}} (V - V_{F B} - \frac{k T}{e}) n - t y p e

(12)

式中， $\hat{ε}$ 为钝化膜相对介电常数 (不锈钢表面膜的 $\hat{ε}$ 约为12^[15~18])，ε₀为真空介电常数，N_A和N_D分别为半导体中的受主和施主密度，e为电子电量 (1.6×10^-19 C)，A为工作电极面积，V为施加的电压，V_FB为平带电位，k为Boltzmann常数，T为温度。界面电容C可通过以下表示：

C = - \frac{1}{ω Z_{I m}}

(13)

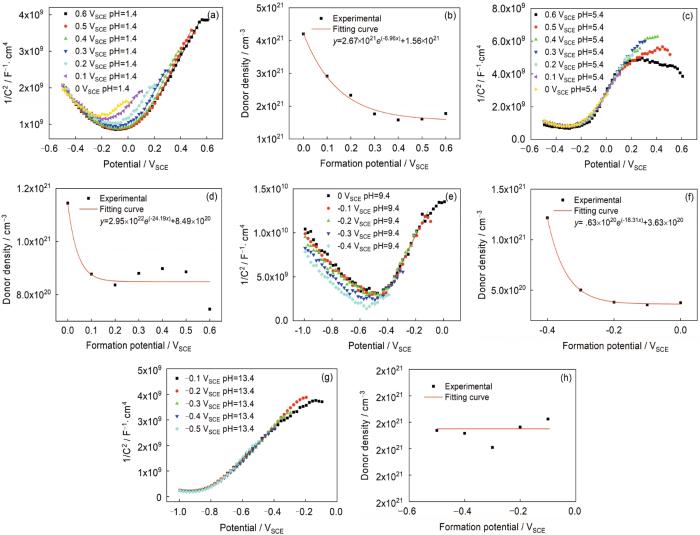
式中，Z_Im是阻抗的虚部，ω=2πf。值得一提的是，M-S分析假定了氧化膜内施主密度的均匀性^[17]，但是已有的研究^{[17, 19~21]}表明这个假设通常是不成立的，因此本研究中M-S分析是半定量分析。图4a, c, e, g所示为304不锈钢在不同pH溶液中钝化膜空间电荷电容与电位的关系。由图可知，在相应实验条件下，当304不锈钢处于钝化区间时，钝化膜电容平方的倒数与电压呈正比例关系，那么根据M-S理论，304不锈钢表面钝化膜呈n型半导体特征。因此，可以认为在金属/钝化膜界面处的主要缺陷是阳离子间隙或氧空位。图4b, d, f, h所示为在不同电位下形成的钝化膜中的施主密度。本文中计算出的施主密度量级为10²¹ cm^-3，与文献[4]的结果相符，并且施主密度随成膜电位升高而降低的趋势也与文献[16,17]一致。因此，施主密度与成膜电位的关系可由公式 (14) 表示，

N_{D} = ω_{1} e x p (- b E) + ω_{2}

(14)

式中， $ω_{1}$ , $ω_{2}$ 和b是常数，它们的值可由实验获得。图4b, d, f, h示出了实验结果的拟合曲线。由图可以看出施主密度随着溶液pH值的升高而明显降低。根据PDM理论，随着pH的升高，膜/溶液界面的间隙溶解速率降低，载流子密度降低。需要注意的是，在pH=13.4的溶液中没有观察到指数下降关系。

图4

图4 304不锈钢在不同pH溶液中施加不同恒电位极化6 h后的Mott-Schottky曲线和阻挡层的施主密度

Fig.4 Mott-Schottky plots (a, c, e, g) and donor densities (b, d, f, h) for the barrier layer formed on 304 stainless steel passivated for 6 h at different formation potentials in pH 1.4 sulfuric acid solution (a, b), pH 5.4 acetate buffer solution (c, d), pH 9.4 borate buffer solution (e, f) and pH 13.4 H₃BO₃+NaOH solution (g, h)

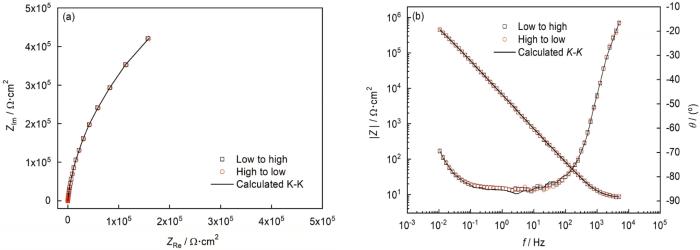
在不同溶液条件下对304不锈钢施加恒电位后进行电化学阻抗分析。在本研究中，在使用阻抗谱前，对阻抗数据的可靠性进行了实验和理论的校验。如图5所示，数据点分别表示频率从高到低 (红色圆形) 扫描的和从低到高 (黑色的正方形) 扫描的阻抗数据，可以看出两个方向的扫描结果完全重合没有出现迟滞。实线表示通过K-K转换获得的理论曲线，可见实验和理论计算也具有很好的一致性。通过以上分析可以确定，本实验条件下钝化膜系统符合线性系统要求，并且具有很好的稳定性。在本实验中使用的阻抗数据都进行了以上所述相同标准的校验，从而保证后面分析结果的准确性。

图5

图5 304不锈钢在pH=1.4溶液中0.5 V_SCE恒电位极化后的EIS和K-K变换曲线

Fig.5 EIS plots (a) and K-K transforms (b) for 304 stainless steel at a potential of 0.5 V_SCE in pH 1.4 solution

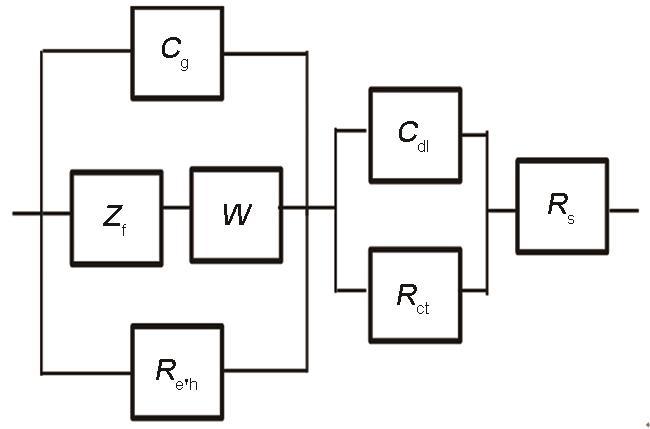
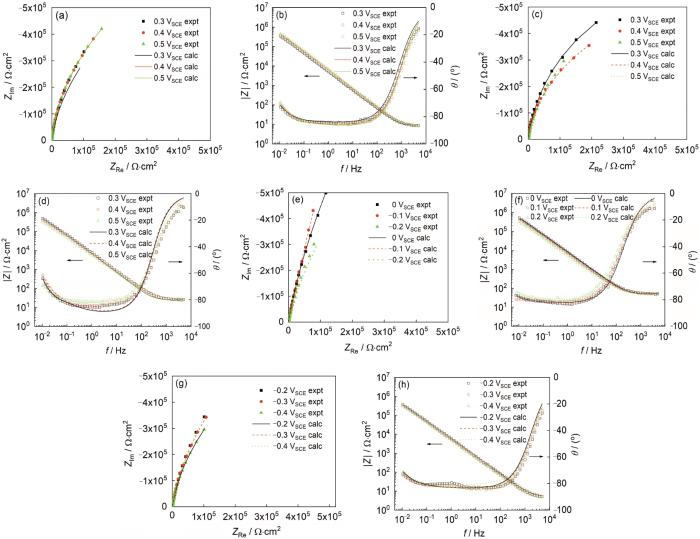
通过遗传算法 (GDE)，将PDM在实验获得的阻抗数据上进行最优化计算，可以拟合出不锈钢腐蚀反应的动力学参数 (比如，反应速率常数，传输系数等)，并且计算值与实验值相符合^{[13, 25]}。在分析电化学阻抗数据时，采用的等效电路图如图6所示。图7b Bode图在低频区是一条直线 (恒相位角阻抗)，对电位不敏感。低频阻抗的恒相位角特性是氧化膜中缺陷迁移的结果，主要是在电场作用下的迁移 (即运动通过迁移而非扩散)。阻抗轨迹对施加电位不敏感表明钝化膜内的电场强度与成膜电位无关，这是PDM重要假设之一，即缺陷在阻挡层内传输的驱动力与所施加的电压无关。从物理角度来讲，由于阻挡层内电子和空穴的Esaki隧穿缓冲效应，施加的电位与阻挡层内的场强无关^{[10, 23]}。这也证明了PDM的恒定电场强度的假设。

图6

图6 拟合阻抗数据的等效电路图

Fig.6 Equivalent circuit used to ﬁt the experimental data of EIS

图7

图7 304不锈钢在不同溶液中施加不同电位极化后的EIS图

Fig.7 Nyquist (a, c, e, g) and Bode (b, d, f, h) plots for 304 stainless steel in pH 1.4 sulfuric acid solution (a, b), pH 5.4 acetate buffer solution (c, d), pH 9.4 H₃BO₃+NaOH solution (e, f) and pH 13.4 H₃BO₃+NaOH solution (g, h) at different applied potentials

进行实验数值最计算优化拟合前，参数α和β分别取值0.338^[3]和-0.01^[6]。参数Ω=14.59 cm³·mol^-1，即假设将Cr₂O₃作为阻挡层主要成分所计算出的摩尔体积。通过第一阶段的优化，获得钝化膜中电场强度ε=2.03×10⁶ V·cm^-1，钝化膜溶解反应中H⁺的反应动力学等级n=0.5，标准状态下ϕ⁰_f/s =-0.01 V。图7比较了在不同的成膜电位下，304不锈钢在不同pH溶液中实验所得的阻抗谱和PDM模拟所得的阻抗谱。实线显示了基于PDM方程和优化确定的参数值计算的最佳拟合结果。可以看出，实验结果与PDM计算结果之间的一致性非常好，表明PDM能够对实验数据进行合理解释。

通过最优化拟合EIS数据获得的参数值，根据PDM中的反应方程，可以精确的模拟实验数据。通过拟合获得的参数列在表2~5中，包括传输系数、基本速率常数、主要点缺陷的扩散系数、稳态钝化膜厚度和电流密度等。由表可见，不同条件下，304不锈钢在整个钝化区间内的钝化膜状态可以用同一组速率常数值和传输系数值来表示，这符合电化学理论。其中，可以看出图1中反应2的速率常数 (k₂) 大于反应3的速率常数 (k₃)。由此可知，在测试电位区间内，间隙阳离子是304不锈钢钝化膜中的主要点缺陷形式，并且由于间隙阳离子的施主特性，钝化膜具有n型半导体特征。

表2 304不锈钢在pH=1.4溶液中不同钝化膜形成电位下PDM最优化模型参数值

Table 2 Calculated values of various parameters from optimization of the PDM based on the experimental impedance data for 304 stainless steel in pH 1.4 solution at different applied potentials

Parameter	0.3 / V	0.4 / V	0.5 / V	Stage optinization
Polarizability α	0.45	0.45	0.44	Second stage optimization
Transfer coeff. α₂	0.23	0.23	0.23	Average of first stage optimization
Transfer coeff. α₃	0.66	0.66	0.66	Average of first stage optimization
Transfer coeff. α₇	0.49	0.49	0.49	Average of first stage optimization
Rate constant $k_{2}^{00} /$ mol·cm^-2·s^-1	4.67×10^-13	4.67×10^-13	4.67×10^-13	Average of first stage optimization
Rate constant $k_{3}^{00}$ / mol·cm^-2·s^-1	3.78×10^-17	3.78×10^-17	3.78×10^-17	Average of first stage optimization
Rate constant $k_{7}^{00}$ / mol·cm^-2·s^-1	6.16×10^-15	6.16×10^-15	6.16×10^-15	Average of first stage optimization
CPE-Y / S·s ^α ·cm^-2	4.18×10^-5	3.92×10^-5	3.86×10^-5	Second stage optimization
CPE-α	0.94	0.95	0.95	Second stage optimization
Warburg coeff. σ / Ω·cm²·s^-0.5	3.03×10⁵	2.14×10⁵	1.56×10⁵	Second stage optimization
Electronic resistance R_{e, h} / Ω·cm²	7.82×10⁶	1.72×10⁷	9.93×10¹²	Second stage optimization
Double layer capacitance C_dl / F·cm^-2	1.51×10^-4	9.56×10^-5	6.91×10^-5	Second stage optimization
Charge transfer resistance R_ct / Ω·cm²	1.75×10⁵	2.88×10⁵	4.22×10^-5	Second stage optimization
Strength of electric field ε / V·cm^-1	2.03×10⁶	2.03×10⁶	2.03×10⁶	Average of first stage optimization
Kinetic order of H⁺n	0.5	0.5	0.5	Average of first stage optimization
Current density I_ss / nA·cm^-2	16.15	20.24	24.56	Second stage optimization
Thickness of barrier layer L_ss / nm	1.24	1.47	1.74	Second stage optimization
Diffusivity of principal defect D / cm²·s^-1	1.34×10^-18	8.64×10^-19	6.43×10^-19	Second stage optimization

表3 304不锈钢在pH=5.4溶液中不同钝化膜形成电位下PDM最优化模型参数值

Table 3 Calculated values of various parameters from optimization of the PDM based on the experimental impedance data for 304 stainless steel in pH=5.4 solution at different applied potentials

Parameter	0.3 / V	0.4 / V	0.5 / V	Stage optinization
Polarizability α	0.34	0.25	0.25	Second stage optimization
Transfer coeff. α₂	0.23	0.23	0.23	Average of first stage optimization
Transfer coeff. α₃	0.66	0.66	0.66	Average of first stage optimization
Transfer coeff. α₇	0.49	0.49	0.49	Average of first stage optimization
Rate constant $k_{2}^{00}$ / mol·cm^-2·s^-1	4.67×10^-13	4.67×10^-13	4.67×10^-13	Average of first stage optimization
Rate constant $k_{3}^{00}$ / mol·cm^-2·s^-1	3.78×10^-17	3.78×10^-17	3.78×10^-17	Average of first stage optimization
Rate constant $k_{7}^{00}$ / mol·cm^-2·s^-1	6.16×10^-15	6.16×10^-15	6.16×10^-15	Average of first stage optimization
CPE-Y / S·s ^α ·cm^-2	7.34×10^-5	3.53×10^-5	4.14×10^-5	Second stage optimization
CPE-α	1	1	0.94	Second stage optimization
Warburg coeff. σ / Ω·cm²·s^-0.5	1.07×10⁴	6.91×10⁴	7.38×10⁴	Second stage optimization
Electronic resistance R_{e, h} / Ω·cm²	3.78×10¹²	7.07×10¹²	7.67×10¹²	Second stage optimization
Double layer capacitance C_dl / F·cm^-2	3.14×10^-5	6.99×10^-5	1.13×10^-4	Second stage optimization
Charge transfer resistance R_ct / Ω·cm²	1.08×10⁶	3.37×10⁵	4.19×10⁵	Second stage optimization
Strength of electric field ε / V·cm^-1	2.03×10⁶	2.03×10⁶	2.03×10⁶	Average of first stage optimization
Kinetic order of H⁺n	0.5	0.5	0.5	Average of first stage optimization
Current density I_ss / nA·cm^-2	15.22	13.4	15.66	Second stage optimization
Thickness of barrier layer L_ss / nm	2.36	2.99	3.33	Second stage optimization
Diffusivity of principal defect D / cm²·s^-1	1.85×10^-10	5.45×10^-19	4.66×10^-19	Second stage optimization

表4 304不锈钢在pH=9.4溶液中不同钝化膜形成电位下PDM最优化模型参数值

Table 4 Calculated values of various parameters from optimization of the PDM based on the experimental impedance data for 304 stainless steel in pH 9.4 solution at different applied potentials

Parameter	0 / V	-0.1 / V	-0.2 / V	Stage optinization
Polarizability α	0.45	0.282624	0.289249	Second stage optimization
Transfer coeff. α₂	0.23	0.23	0.23	Average of first stage optimization
Transfer coeff. α₃	0.66	0.66	0.66	Average of first stage optimization
Transfer coeff. α₇	0.49	0.49	0.49	Average of first stage optimization
Rate constant $k_{2}^{00}$ / mol·cm^-2·s^-1	4.67×10^-13	4.67×10^-13	4.67×10^-13	Average of first stage optimization
Rate constant $k_{3}^{00}$ / mol·cm^-2·s^-1	3.78×10^-17	3.78×10^-17	3.78×10^-17	Average of first stage optimization
Rate constant $k_{7}^{00}$ / mol·cm^-2·s^-1	6.16×10^-15	6.16×10^-15	6.16×10^-15	Average of first stage optimization
CPE-Y (S·s ^α ·cm^-2	2.39×10^-5	2.70×10^-5	3.97×10^-5	Second stage optimization
CPE-α	0.91	0.91	0.89	Second stage optimization
Warburg coeff. σ / Ω·cm²·s^-0.5	8.48×10⁵	3.82×10⁵	6.28×10⁵	Second stage optimization
Electronic resistance R_{e, h} / Ω·cm²	1.00×10¹³	9.81×10¹²	9.99×10¹²	Second stage optimization
Double layer capacitance C_dl / F·cm^-2	2.23×10^-4	48.99×10^-4	2.32×10^-4	Second stage optimization
Charge transfer resistance R_ct / Ω·cm²	1.18×10⁵	2.03×10⁴	6.02×10⁴	Second stage optimization
Strength of electric field ε / V·cm^-1	2.03×10⁶	2.03×10⁶	2.03×10⁶	Average of first stage optimization
Kinetic order of H⁺n	0.5	0.5	0.5	Average of first stage optimization
Current density I_ss / nA·cm^-2	13.93	9.91	8.62	Second stage optimization
Thickness of barrier layer L_ss / nm	2.08	1.99	1.66	Second stage optimization
Diffusivity of principal defect D / cm²·s^-1	2.32×10^-18	1.08×10^-18	1.34×10^-18	Second stage optimization

表5 304不锈钢在pH=13.4溶液中不同钝化膜形成电位下PDM最优化模型参数值

Table 5 Calculated values of various parameters from optimization of the PDM based on the experimental impedance data for 304 stainless steel in pH 13.4 solution at different applied potentials

Parameter	-0.2 / V	-0.3 / V	-0.4 / V	Stage optinization
Polarizability α	0.394221	0.449973	0.45	Second stage optimization
Transfer coeff. α₂	0.23	0.23	0.23	Average of first stage optimization
Transfer coeff. α₃	0.66	0.66	0.66	Average of first stage optimization
Transfer coeff. α₇	0.49	0.49	0.49	Average of first stage optimization
Rate constant $k_{2}^{00}$ / mol·cm^-2·s^-1	4.67×10^-13	4.67×10^-13	4.67×10^-13	Average of first stage optimization
Rate constant $k_{3}^{00}$ / mol·cm^-2·s^-1	3.78×10^-17	3.78×10^-17	3.78×10^-17	Average of first stage optimization
Rate constant $k_{7}^{00}$ / mol·cm^-2·s^-1	6.16×10^-15	6.16×10^-15	6.16×10^-15	Average of first stage optimization
CPE-Y / S·s ^α ·cm^-2	4.08×10^-5	3.65×10^-5	3.97×10^-5	Second stage optimization
CPE-α	0.88	0.92	0.92	Second stage optimization
Warburg coeff. σ / Ω·cm²·s^-0.5	3.99×10⁵	2.52×10⁵	2.26×10⁵	Second stage optimization
Electronic resistance R_{e, h} / Ω·cm²	8.28×10¹²	8.28×10¹²	7.42×10¹²	Second stage optimization
Double layer capacitance C_dl / F·cm^-2	1.35×10^-4	1.54×10^-4	2.04×10^-4	Second stage optimization
Charge transfer resistance R_ct / Ω·cm²	2.25×10⁵	1.83×10⁵	1.24×10⁵	Second stage optimization
Strength of electric field ε / V·cm^-1	2.03×10⁶	2.03×10⁶	2.03×10⁶	Average of first stage optimization
Kinetic order of H⁺n	0.5	0.5	0.5	Average of first stage optimization
Current density I_ss / nA·cm^-2	1.15	0.93	0.74	Second stage optimization
Thickness of barrier layer L_ss / nm	2.39	2.15	1.93	Second stage optimization
Diffusivity of principal defect D / cm²·s^-1	5.21×10^-18	1.54×10^-18	7.30×10^-19	Second stage optimization

表2~5中列出了计算的钝化膜内层的厚度。随着极化电位的增大，计算的阻挡层厚度也呈增加趋势。在本研究中，304不锈钢表面的钝化膜内层厚度计算结果为1.24~3.33 nm。这与文献报导值^[26~29]相比数值较小，本文计算膜厚与文献测量膜厚之间的差异可能是由于实验测量的膜厚包括多孔腐蚀产物层 (钝化膜外层) 造成的，而外层通常比致密阻挡层厚，而电化学测试响应信号几乎全部由致密阻挡层贡献^[29]。表中所得的钝化膜的厚度对应不同的施加电位，以电位为横坐标钝化膜厚度为纵坐标求斜率可估算出不同pH条件下钝化膜生长速率，然后求取平均值得出生长速率为2.94 nm·V^-1，略大于室温下钝化膜生长速率1.9~2.5 nm·V^{-1 [5]}。同样，这里计算出的稳态电流密度 (I_ss ) 基本上与电位无关，并且接近于图3中的实验值。基于PDM理论，在金属/钝化膜界面生成的点缺陷向钝化膜/溶液界面传输的驱动力主要是电场。此外，计算所得间隙阳离子的扩散系数值约为10^-18~10^-20 cm²·s^-1，符合文献的报导值^[26~29]。

3 结论

动电位极化实验表明304不锈钢在pH 1.4~13.4溶液中均有较宽的钝化区间。在稳态条件下，电流密度不受施加电位的影响，而钝化膜厚度以2.94 nm·V^-1的速度随着电位的增加而增厚。Mott-Schottky测试表明了304不锈钢表面钝化膜是n型半导体，并计算出了施主密度在不同pH和电位条件下的数值，计算结果表明阻挡层内的施主密度随着成膜电位增加呈指数型下降，其值也随着pH值的增加而降低。

通过点缺陷模型优化了实验获得的304不锈钢钝化膜电化学阻抗谱数据，推导出其在溶液中钝化状态的反应动力学参数的数值解，利用这些参数可以预测稳态和瞬态的钝化膜生长过程。本研究获得的动力学数据表明，点缺陷模型能够合理解释304不锈钢的钝化状态，该模型可以预测不锈钢在特定条件下长期的均匀腐蚀行为。

致谢

感谢加州大学伯克利分校Digby Macdonald教授对论文内容的讨论与指导。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Gai

X P

, Lei

, Cui

Z Y

Pitting corrosion behavior of 304 stainless steel in simulated concrete pore solutions

[J]. J. Chin. Soc. Corros. Prot., 2021, 41: 646

盖喜鹏, 雷黎, 崔中雨.

304不锈钢在模拟混凝土孔隙液中的点蚀行为研究

[J]. 中国腐蚀与防护学报, 2021, 41: 646

采用电化学测试方法研究了不同Cl-浓度下，304不锈钢在两种模拟混凝土孔隙液中的点蚀行为，确定了304不锈钢的临界Cl-浓度；采用SEM观察了304不锈钢表面钝化膜在临界Cl-浓度前后的状态。结果表明，通过动电位极化和恒电位阻抗方法确定了304不锈钢的临界Cl-浓度，且数值基本一致，并SEM观测结果相一致；而开路电位下的阻抗测试并不能确定临界Cl-浓度。

[2]

Liu

X Y

, Zhao

Y Z

, Zhang

, et al.

Effect of chloride concentration in a simulated concrete pore solution on metastable pitting of 304 stainless steel

[J]. J. Chin. Soc. Corros. Prot., 2021, 41: 195

刘欣怡, 赵亚州, 张欢等.

混凝土孔隙液中Cl^-浓度对304不锈钢亚稳态点蚀的影响

[J]. 中国腐蚀与防护学报, 2021, 41: 195

通过动电位极化和恒电位极化研究了Cl-浓度对304不锈钢在模拟混凝土孔隙液 (pH 12.6) 中亚稳态点蚀的影响，并利用极值统计分布研究了亚稳态点蚀的峰值电流密度 (Ipeak)，亚稳态点蚀半径 (rpit)，亚稳态点蚀稳定性乘积 (Ipeak·rpit) 以及单个亚稳态点蚀的生长时间 (tgrow)，再钝化时间 (trep)，生长率 (Kgrow) 和再钝化率 (Krep)。结果表明，在碱性介质中，Cl-浓度增加会促使亚稳态点蚀更易转变为稳定点蚀。

[3]

, Li

, Wang

S G

, et al.

Electrochemical corrosion behavior of nanocrystallized bulk 304 stainless steel

[J]. Electrochim. Acta, 2006, 52: 760

[4]

Yang

S F

, Macdonald

D D

Theoretical and experimental studies of the pitting of type 316L stainless steel in borate buffer solution containing nitrate ion

[J]. Electrochim. Acta, 2007, 52: 1871

[5]

Nicic

, Macdonald

D D

The passivity of Type 316L stainless steel in borate buffer solution

[J]. J. Nucl. Mater., 2008, 379: 54

[6]

Zhang

Y C

, Macdonald

D D

, Urquidi-Macdonald

, et al.

Passivity breakdown on AISI Type 403 stainless steel in chloride-containing borate buffer solution

[J]. Corros. Sci., 2006, 48: 3812

[7]

Chao

C Y

, Lin

L F

, Macdonald

D D

A point defect model for anodic passive films: I. Film growth kinetics

[J]. J. Electrochem. Soc., 1981, 128: 1187

[8]

Lin

L F

, Chao

C Y

, Macdonald

D D

A point defect model for anodic passive films: II. Chemical breakdown and pit initiation

[J]. J. Electrochem. Soc., 1981, 128: 1194

DOI

[9]

Chao

C Y

, Lin

L F

, Macdonald

D D

A point defect model for anodic passive films: III. Impedance response

[J]. J. Electrochem. Soc., 1982, 129: 1874

DOI [本文引用: 2]

[10]

Macdonald

D D

, Smedley

S I

An electrochemical impedance analysis of passive films on nickel (111) in phosphate buffer solutions

[J]. Electrochim. Acta, 1990, 35: 1949

[11]

Urquidi-Macdonald

, Real

, Macdonald

D D

Application of Kramers-Kronig transforms in the analysis of electrochemical impedance data: II. Transformations in the complex plane

[J]. J. Electrochem. Soc., 1986, 133: 2018

[12]

Macdonald

D D

Point defect model of the passive state

[A]. MacdonaldJ R, BarsukovE. Impedance Spectroscopy Theory, Experiment, and Applications [M]. 2nd ed., New York: Wiley-Interscience, 2005: 382

[13]

Sharifi-Asl

, Taylor

M L

, Lu

Z J

, et al.

Modeling of the electrochemical impedance spectroscopic behavior of passive iron using a genetic algorithm approach

[J]. Electrochim. Acta, 2013, 102: 161

[14]

Macdonald

D D

The point defect model for the passive state

[J]. J. Electrochem. Soc., 1992, 139: 3434

[15]

Hakiki

N E

, Da Cunha Belo

, Simões

A M P

, et al.

Semiconducting properties of passive films formed on stainless steels: influence of the alloying elements

[J]. J. Electrochem. Soc., 1998, 145: 3821

[16]

Di Paola

Semiconducting properties of passive films on stainless steels

[J]. Electrochim. Acta, 1989, 34: 203

[17]

Stimming

, Schultze

J W

The capacity of passivated iron electrodes and the band structure of the passive layer

[J]. Ber. Bunsenges. Phys. Chem., 1976, 80: 1297

DOI URL [本文引用: 3]

[18]

Gaben

, Vuillemin

, Oltra

Influence of the chemical composition and electronic structure of passive films grown on 316L SS on their transient electrochemical behavior

[J]. J. Electrochem. Soc., 2004, 151: B595

[19]

Wagner

Models for lattice defects in oxide layers on passivated iron and nickel

[J]. Ber. Bunsenges. Phys. Chem., 1973, 77: 1090

[20]

Goossens

, Vazquez

, Macdonald

D D

The nature of electronic states in anodic zirconium oxide films part 1: the potential distribution

[J]. Electrochim. Acta, 1996, 41: 35

[21]

Macdonald

D D

, Sikora

The kinetics of growth of the passive film on tungsten in acidic phosphate solutions

[J]. Electrochim. Acta, 1998, 43: 2851

[22]

Cheng

X Q

, Li

X G

, Yang

L X

, et al.

Corrosion resistance of 316L stainless steel in acetic acid by EIS and Mott-Schottky

[J]. J. Wuhan Univ. Technol.: Mater. Sci. Ed., 2008, 23: 574

[23]

Sikora

, Macdonald

D D

Nature of the passive film on nickel

[J]. Electrochim. Acta, 2002, 48: 69

[24]

Macdonald

D D

, Urquidi-Macdonald

Kramers-Kronig transformation of constant phase impedances

[J]. J. Electrochem. Soc., 1990, 137: 515

DOI

[25]

Sharifi-Asl

, Macdonald

D D

, Almarzooqi

, et al.

A comprehensive electrochemical impedance spectroscopic study of passive carbon steel in concrete pore water

[J]. J. Electrochem. Soc., 2013, 160: C316

[26]

Ferreira

M G S

, Dawson

J L

Electrochemical studies of the passive film on 316 stainless steel in chloride media

[J]. J. Electrochem. Soc., 1985, 132: 760

DOI [本文引用: 2]

[27]

Mohammadi

, Nickchi

, Attar

M M

, et al.

EIS study of potentiostatically formed passive film on 304 stainless steel

[J]. Electrochim. Acta, 2011, 56: 8727

[28]

Luo

, Dong

C F

, Xiao

, et al.

Characterization of passive film on 2205 duplex stainless steel in sodium thiosulphate solution

[J]. Appl. Surf. Sci., 2011, 258: 631