金属学报 2014 , 50 (1): 110-120 https://doi.org/10.3724/SP.J.1037.2013.00308

晶界位错运动与位错反应过程的晶体相场模拟^*

高英俊¹^,²^,, 卢成健¹^,³, 黄礼琳¹, 罗志荣¹^,³, 黄创高¹^,²

1 广西大学物理科学与工程技术学院, 南宁 530004
2 广西大学广西有色金属及特色材料加工重点实验室, 南宁 530004
3 玉林师范学院物理科学与工程技术学院, 玉林 537000

PHASE FIELD CRYSTAL SIMULATION OF DISLOCA- TION MOVEMENT AND REACTION

GAO Yingjun¹^,²^,, LU Chengjian¹^,³, HUANG Lilin¹, LUO Zhirong¹^,³, HUANG Chuanggao¹^,²

1 College of Physics Science and Engineering, Guangxi University, Nanning 530004
2 Guangxi Key Laboratory for Non-ferrous Metal and Featured Materials, Guangxi University, Nanning 530004
3 Institute of Physics Science and Engineering Technology, Yulin Normal University, Yulin 537000

中图分类号: TG111.2

通讯作者: Correspondent: GAO Yingjun, professor, Tel: (0771)3232666, E-mail: gaoyj@gxu.edu.cn

收稿日期: 2013-06-4

修回日期: 2013-06-4

网络出版日期: --

基金资助: * 国家自然科学基金项目51161003和50661001，广西自然科学基金重点项目2012GXNSFDA053001，广西大学广西有色金属及特色材料加工重点实验室开放基金GXKFJ12-01及广西大学科研基金项目XJZ110611资助

作者简介:

高英俊, 男, 1962年生, 教授

展开

摘要

采用晶体相场模型模拟了小角度对称倾转晶界结构及其在外加应力作用下的晶界演化消失过程, 从位错的运动形式和体系自由能的变化, 分析晶界的消失过程和位错的反应机理, 并计算了位错分解的激活能. 研究表明, 具有二维三角晶格原子点阵结构形成的小角度对称倾转晶界是由配对的双位错按直线规则排列构成, 可以看成由2套位错Burgers矢量组成. 晶界的消失演化过程主要分为6个特征阶段, 包括如下几方面的特征过程: 首先晶界位错攀移, 然后发生位错分解, 晶界发射位错, 位错由攀移运动转化为作滑移运动；接着滑移位错穿过晶粒内部, 直到对面晶界上湮没, 即被晶界吸收与合并；剩余的晶界位错继续作攀移运动, 然后又出现位错分解, 晶界再次发射位错, 使得位错转为作滑移运动, 与其它作滑移运动的位错在晶内相遇湮没消失. 最后, 所有晶界和位错全部消失, 双晶结构变成为完整的单晶结构. 应用三角晶系的点阵位错的2套基本Burgers矢量的组合, 可以有效地表示位错的发射、分解、合并、吸收、湮没的反应过程, 并能够揭示出这些反应过程的新Burgers矢量的产生和原有的Burgers矢量的消失, 以及Burgers矢量方向发生变化的机理.

关键词： 晶界 ; 位错反应 ; 应变 ; 晶体相场模型

Abstract

Transformations of grain boundaries often strongly influence both the structure and the properties of polycrystalline and nanocrystalline materials. Thus, plastic deformation processes in fine-grained polycrystals and nanocrystalline solids are associated with transformations of grain boundaries, which crucially affect the structure and mechanical characteristics of such solids. Motion of grain boundary dislocations in plastically deformed materials is commonly considered to be the absorption of lattice dislocations by grain boundaries. In order to reveal the mechanism of motion of a low-angle symmetric tilt grain boundary (STGB) associated with the emission and absorption of lattice dislocation, the emission and evolution of a STGB under strain were simulated by phase-field crystal (PFC) model. The decay of STGB and dislocation reactions of separation, annihilation and mergence and their mechanisms were analyzed from the energy point of view, furthermore, the active energy of the dislocation separation was calculated. The research results show that the low-angle STGB is composed of pair dislocations in a line arrangement in two dimensions of triangular atomic lattice, in which there are two sets of basic Burgers vectors. The evolution process of STGB decay can be divided into six typical stages which includes the detail features as: dislocation climbs firstly along the STGB under strain, then the dislocation occurs to break up into two new dislocations after it gets enough energy to overcome the active potential barrier of dislocation, at this time the STGB emits pair dislocations to move in gliding in grain instead of climbing along STGB; gliding for while, the dislocation crosses the grain until it is annihilated by another dislocation at the STGB right in the front, i.e. the Grain boundary absorbs or merges the gliding dislocation. The remain of dislocation in the STGB can still climb along the grain boundary in which splits off again into two dislocations when it gets enough energy, at the same time it looks as if STGB emits the dislocations and changes the dislocation movement from climbing to gliding again. The dislocation continues gliding until it meets another gliding dislocation in grain to be annihilated, finally the total dislocations are annihilated and the STGB disappears. The two grain systems with STGB become one grain system. The two sets of basic Burgers vectors of lattice dislocation in triangular lattice can validly be used to express the dislocation reaction of emission, separation, mergence, absorption, annihilation, and also can reveal the creation of new Burgers vector and the annihilation of old Burgers vectors and mechanism of the directional change of Burgers vectors during the dislocation reaction.

Keywords： grain boundary ; dislocation reaction ; strain ; phase-field crystal model

PDF (13829KB) 元数据多维度评价相关文章收藏文章

本文引用格式导出 EndNote Ris Bibtex

高英俊, 卢成健, 黄礼琳, 罗志荣, 黄创高. 晶界位错运动与位错反应过程的晶体相场模拟^*[J]. , 2014, 50(1): 110-120 https://doi.org/10.3724/SP.J.1037.2013.00308

GAO Yingjun, LU Chengjian, HUANG Lilin, LUO Zhirong, HUANG Chuanggao. PHASE FIELD CRYSTAL SIMULATION OF DISLOCA- TION MOVEMENT AND REACTION[J]. 金属学报, 2014, 50(1): 110-120 https://doi.org/10.3724/SP.J.1037.2013.00308

晶体材料通常由大量晶粒组成, 晶界是取向不同的晶粒之间的交界面. 小角度晶界指位向差值小于10°的晶界^[1,2], 由一系列位错按特定方式排列而成. 位错会引起其附近晶体点阵结构发生畸变^[2]. 在稳定的环境条件下, 晶界(包括亚晶界)可以保持稳定的结构, 而在外加应力作用下位错会发生运动以致晶界(亚晶界)迁移甚至湮没^[3-6]. 晶界的结构和迁移方式对晶粒长大特别是冷加工金属材料的退火有重要影响^[7]. 晶界迁移过程涉及的原子运动比较快, 且在非平衡条件下进行, 使得对晶界迁移过程的位错, 无论实验研究还是理论处理都比较困难. 目前的实验条件较难实时观察晶界、亚晶界上位错的运动, 以及位错反应过程, 借助计算机模拟则可以弥补实验的不足. 近几年基于密度泛函理论模型提出的晶体相场(PFC)方法^[8-11], 优势在于能够在扩散时间尺度(10^-6s)描述纳米尺度的原子的缺陷运动, 相对于分子动力学(MD)方法在时间尺度上具有一定的优势. 与传统相场方法^[12-14]不同, 采用最新发展的PFC方法不仅能够用来研究纳米尺度下材料的微结构, 而且还能够研究扩散时间尺度的位错运动及其对晶界的影响^[11]. 目前, PFC方法已应用于研究位错和晶界的迁移^[11]以及小角度对称倾转亚晶界湮没的过程^[15,16]、纳米孪晶^[17]、多晶凝固^[18]、晶体外延生长^[19,20]、结构相变^[21,22]、晶界熔解^[23]、裂纹扩展^[24]等现象. 本工作应用PFC方法模拟晶界的位错运动和相互作用, 分析位错的运动和自由能变化之间的内在联系, 揭示位错运动、位错反应形式以及位错的Burgers矢量变化和能量变化规律.

1 晶体相场模型

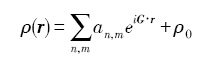对于固态金属材料, 其原子呈规则周期性排列. 因此, 要求相场变量必须能够反映原子周期性排列的特征. PFC模型通过引入具有周期结构特征的原子密度相场变量构建自由能密度函数^[9], 能够揭示晶体学结构特性以及原子尺度的行为. 在引入周期性相场变量中, 局域位置的最大值对应于原子的位置, 而液相中的原子位置随时间随机变化, 取时间平均可看成为常量. 按照这2方面要求, 可用原子密度场函数ρ(r)作为相场变量, 其表达式可写成^[9]:

(1)

式中, a_n_,_m为Fourier系数, $G$ 为倒格矢, $r$ 为空间位置矢量. 式(1)中右边第一项反映晶格原子的周期排列结构特征, 第二项 $ρ_{0}$ 为原子平均密度, 反映液相的原子均匀无序特征, 平均值为常量. 此时体系无量纲的自由能函数F可以写成^[9]:

(2) $F = \int_{}^{} \{\frac{ρ}{2} [γ + (1 + \nabla^{2})^{2}] ρ + \frac{ρ^{4}}{4}\} d r$

式中, $γ$ 是反映体系温度的参数. 该能量模型自洽地包含了晶体结构的物理特征, 例如晶粒取向、弹性变形、塑性变形等.

保守的原子密度场变量的演化可用与时间相关的Cahn-Hilliard动力学方程描述^[9]:

(3) $\frac{\partial ρ}{\partial t} = ▽^{2} \frac{δ F}{δ ρ} = ▽^{2} (γ ρ + (1 + ▽^{2})^{2} ρ + ρ^{3})$

式中, t为时间变量. 由式(2)得到稳定的三角相的二维单模近似解ρ为^[9]:

(4) $ρ = A [c o s (q x) c o s (q y / \sqrt{3}) - c o s (2 q y / \sqrt{3}) / 2] + ρ_{0}$

式中, 振幅 $A = 4 / 5 (ρ_{0} + 1 / 3 \sqrt{- 15 r - 36 ρ_{0}^{2}})$ , 波矢 $q = \sqrt{3} / 2$ , r为r的模.

由式(2)表示的自由能极小值, 得到对应的3种平衡相, 即液相(Liquid), 条状相(Stripe)和三角相(Triangular). 在二维系统中, 通过单模近似可以获得平衡时各相的自由能密度, 再利用自由能公切线法确定相图^[15].

2计算方法

2.1 数值计算与初始条件

对式(3)采用半隐式Fourier谱方法^[25]求解, 其离散形式为:

(5) $\frac{ρ_{k, t + Δ t} - ρ_{k, t}}{Δ t} = - k^{2} {[γ + (1 - k^{2})^{2}] ρ_{k, t + Δ t} + {(ρ)}_{k, t}^{3}}$

整理后得:

(6) $ρ_{k, t + Δ t} = [ρ_{k, t} - k^{2} (ρ_{k, t}^{3}) Δ t] / {1 + k^{2} [γ + (1 - k^{2})^{2}] Δ t}$

式中, $ρ_{k, t + Δ t}$ 为Fourier空间t+Δt时刻的原子密度, $ρ_{k, t}$ 为Fourier空间t时刻的原子密度, $k$ 为Fourier空间的波矢, k为k的模.

在本文的模拟中, 采用二维三角晶系表征面心立方(fcc)晶体的(111)面的原子点阵结构. 选取模拟参数 $ρ_{0}$ =0.285, $γ$ =-0.25, 取空间步长为Δx=Δy=π/4, 时间步长为Δt=0.5. 边界条件为周期性边界条件. 初始条件按如下方法设置: 对于周期性的计算区域 $L_{x} \times L_{y} = 256 Δ x \times 256 Δ y$ , 设置成4个不同区域: 2个晶粒区域和2个初始液相区域, 液相区域设置成较窄的带状区域, 宽度为 $d_{0}$ , 2个晶粒的初始位向差为θ. 运用式(4)使三角晶相的取向在晶粒I区域 $0 < x < 1 / 4 (L_{x} - 2 d_{0})$ 和 $1 / 4 (3 L_{x} + 2 d_{0}) < x < L_{x}$ 范围内为θ/2, 在中间(晶粒II)区域 $1 / 4 (L_{x} + 2 d_{0}) < x < 3 / 4 (L_{x} - 2 d_{0})$ 范围内为-θ /2, 其中 $0 < y < L_{y}^{}$ . 为了让2晶粒之间的晶界衔接得更好, 在2个晶粒之间的带状液相区宽度为10, 并使2个晶粒交界边沿原子初始排列做到最佳匹配状态. 经过300步的时间弛豫, 液相区域结晶出三角固相原子排列, 获得稳定的对称倾侧晶界.

2.2 外应力的施加

在外加应力作用下, 晶粒会发生变形, 引起晶界和位错运动变化. 在二维体系的变形过程中采用等面积不变模型^[26,27], 则有

(7) $Δ x Δ y = Δ x' Δ y'$

式中, Δx和Δy为变形前的空间步长, $Δ x'$ 和 $Δ y'$ 为变形后的空间步长. 设应变速率为 $\dot{ε}$ , 应变量 $ε = \dot{ε} n Δ t$ (n为时间步数, Δt为时间步长). 设在x方向上给体系一个拉应力, 则有:

(8) $Δ x' = (1 + ε) Δ x = Δ x + n \dot{ε} Δ x Δ t$

(9) $Δ y' = Δ y / (1 + ε) = Δ y / (1 + n \dot{ε} Δ t)$

由此可见, 在y方向上体系受到一个压应力. 应变速率设为 $\dot{ε} = 6 \times 10^{- 6}$ s^-1. 详细的二维拉伸变形模拟的数值算法见文献[26,28].

3 结果与分析

3.1 晶界的位错结构

对于取向差为6.7°的对称倾侧晶界, 由图1a所示的对称倾侧晶界结构可见, 晶界由配对的刃位错组按直线等距离规则排列而构成. 把2个配对的晶界刃位错组称为晶界位错对. 对于三角晶系点阵结构的晶格原子排列, 组成晶界位错对的2个刃位错的多余原子排列平面之间的夹角近似为60°, 如图1所示. 实际上, 如图1a所示, 这种对称倾侧晶界的位错对可看成由2套Burgers矢量的刃位错配对组合而成, 这2套Burgers矢量是基本Burgers矢量. 对于二维三角晶系晶格点阵原子排列结构, 最多可以有6套Burgers矢量^[29], 其它4个方向的Burgers矢量可由这2套Burgers基矢组合表示. 晶界上的位错排列的2套Burgers基矢方向与晶界法向的夹角分别为θ/2和-θ/2, 且关于晶界法向对称. 同时, 这2套Burgers矢量的大小相等, 并且, 这2套Burgers基矢排列的位错间距也相等, 即满足位错间距 $d$ 与位错Burgers矢量b, 取向差θ之间的关系为^[1,2]:

(10) $d_{1} = d_{2} = d = \frac{b}{2 s i n (\frac{θ}{2})} \approx \frac{b}{θ}$

式中, $d_{1}$ 和 $d_{2}$ 表示方向不同的2套Burgers矢量位错排列的间距, b为矢量b的模. 对于小角对称倾侧晶界, 位错间距 $d$ 与角度θ成反比.

3.2 外应力作用下的位错运动

3.2.1晶界消失过程在外加应力作用下晶粒发生变形, 整个晶界湮没消失过程主要分为6个特征阶段, 各阶段出现了不同形式的位错运动和位错反应现象. 晶界湮没过程如图1a~i所示, 体系自由能随时间变化的曲线如图2所示.

显示原图| 下载原图ZIP| 生成PPT

图1

Fig.1 取向差θ=6.7°时的晶界湮没过程模拟

图1中晶界湮没过程的6个特征阶段与图2的自由能-时间步曲线的6个不同曲线阶段对应. 第1阶段为位错沿晶界攀移, 位错积累更多的应变能量, 如图2所示的曲线第一阶段的能量增加过程. 当晶界位错积累了足够的能量后, 在晶界上发生分解, 如图1a中的位错对A分解成图1b中的位错A₁和A₂, 图1a中的位错对D分解成图1b中的位错D₁和D₂. 第2阶段如图1b~d示, 晶界分解而发射出来的位错滑移到晶粒内部, 与Burgers矢量相反的位错相遇湮没, 如图1c所示的位错A₂和D₁相遇后湮没消失. 晶粒内部所有的位错相遇湮没标志着第2阶段结束, 此时体系的位错数量明显减少, 晶粒内部没有位错, 晶界上的位错数量也减少. 第3阶段为晶界上尚未分解的2对晶界位错对在应变作用下继续攀移累积能量, 直到位错B脱离晶界束缚而发生分解, 这一过程能量增加的幅度较小, 如图1d和e中的位错B分解为位错B₁和B₂. 第4阶段为分解的滑移位错(B₁和B₂)运动到对面晶界而依次被晶界吸收的过程, 如图1e~g. 在这个过程中, 首先是位错B₁滑移到对面晶界, 遇到晶界上的位错C而组合成一个复合位错B₁C, 组合成的新位错组B₁C的位置明显偏离了原来晶界的位置, 或者说由于位错的相互吸引作用而使晶界在吸收位错过程向着位错方向产生偏移或转动, 以减小晶界的位向差. 图1f中的位错B₂的Burgers矢量与其右边晶界处位错Burgers矢量包含方向相反的分量, 这两个位错是相互吸引的, 结果也使该处的晶界发生了偏移. 如图1f和g所示, 位错B₂继续滑移至复合位错B₁C处, 两者相遇湮没, 完成了晶界再次吸收位错的过程. 第5阶段与第1阶段类似, 剩余的2个晶界位错对在应力作用下沿着晶界继续攀移, 如图1g和h所示, 由图2中的能量曲线gh段反映了此过程的能量增加. 第6阶段与第2阶段类似, 这时, 位错对在晶界处分解、滑移至晶粒内, 所有的位错都会在晶粒内相遇而全部湮没, 晶界湮没结束, 形成1个完整单晶体结构, 如图1h和i所示.

显示原图| 下载原图ZIP| 生成PPT

图2

Fig.2 晶界位向差θ=6.7°的体系自由能随时间变化的曲线

可以从能量的角度分析位错运动和晶界湮没机制. 从整个体系来看, 体系自由能包含晶界的位错能和畸变能, 位错密度越高, 体系畸变程度越大, 则体系的自由能就越高. 图1a~i的位错运动湮没过程与图2曲线的变化具有对应关系: 图1a的时间步数与图2曲线上a点的时间步数对应, 图1b的时间步数与图2曲线上b点的时间步数对应(后面图1与图2曲线上各点的对应情形, 可依此类推). 由图2可见晶界湮没过程, 体系自由能出现了3个极大值和3个极小值, 虚线处于体系自由能极大值位置, 对应位错脱离晶界; 极小值位置对应前一个阶段结束和后一个阶段开始, 圆圈表示晶界湮没完成. 第1阶段如图1a和图2中a点所在的曲线段, 在应力作用下, 位错能量积累使体系自由能增至极大, 如图2中第1条垂直虚线处所示; 第2阶段如图2曲线b, c和d点所在线段, 晶界位错开始分解, 然后脱离晶界滑移至晶粒内. 位错在晶粒内继续滑移, 使体系畸变程度变小, 于是, 体系自由能降低. 当晶粒内的位错全部相遇湮没时, 体系自由能就降为第1个极小值, 如图2曲线上的d点; 接着是第3阶段, 少量已分解的位错在晶界上攀移, 在应变作用下, 其自由能上升至足够大以至可以脱离晶界束缚而滑移到晶粒内, 如图2中第2条垂直虚线和e点, 这一阶段相对于第一阶段的体系能量增加的幅度要小很多；第4阶段为少量位错滑移至对面晶界被晶界吸收(即位错在晶界湮没), 使得自由能下降, 如图2曲线上的f点和g点, g点对应吸收完成, 自由能降至极小值；第5, 6阶段分别与第1, 2阶段类似, 不过这时余下的晶界位错对都参与攀移, 当能量增幅较大, 达到临界值时, 晶界位错对发生分离而脱离晶界, 然后迅速滑移至晶粒内部与其它位错相遇而全部湮没, 完成晶界湮没全过程.

3.2.2位错的攀移和滑移运动位错运动分为攀移和滑移. 滑移面是由位错线和Burgers矢量决定的平面, 在图1a~i中, 各位错线垂直纸面, 位错Burgers矢量如图中小箭头所示. 滑移是位错沿滑移面的运动, 而攀移是位错在垂直于滑移面方向上的运动, 所以位错沿晶界的运动是攀移, 位错在晶粒内的运动是滑移.

在二维三角晶系晶格原子点阵中, 对称倾侧晶界的位错对结构, 就类似于三维fcc结构的 $(1 \bar{1} 1)$ 和 $(\bar{1} 11)$ 平面交汇处的Lomer-Collrell (L-C)锁^[1,2], 其由一对不全位错构成. 该锁结构使得位错不能滑移运动, 只能在外应力的作用下作攀移运动, 直到达到临界应变值时, 才可发生位错分解反应, 才能启动滑移系, 位错才能滑移运动.

综合图1a~i可以推断, 在拉应力的作用下晶界位错对产生负攀移, 沿晶界的攀移使晶界的能量上升, 脱离晶界的位错滑移使晶界的能量下降. 在相同应力作用下, 位错的攀移速率和滑移速率是不一样的. 以图1a和b中沿晶界攀移的位错B的位置变化及相应的时间步数变化计算得到其位移与时间步数变化之比, 即攀移速率V₁为:

(11) $V_{1} = 1.913 \times 10^{- 4} (a / n)$

式中, a为晶格常数. 以图1b和c中在晶粒内滑移的位错A₂的位置变化及相应的时间步数变化计算得到其滑移速率V₂为:

(12) $V_{2} = 6.184 \times 10^{- 3} (a / n)$

2者之比V₂/V₁=32.3, 可见位错的滑移速率远大于攀移速率. 由图2可见, 位错分解阶段的曲线要比位错攀移阶段的曲线要陡. 考虑到取向差为小角度, 且位错Burgers矢量只出现在原子密排3个方向上, 则位错分解前的Burgers矢量近似与晶界垂直, 位错分解后的Burgers矢量方向与晶界法向的夹角约为60°, 所以位错脱离晶界后在与晶界法向成约60°的方向上滑移.

3.3位错反应的能量变化

3.3.1 位错在晶界的分解晶界上的位错对在外应力作用下首先发生攀移运动, 使得晶界位错的畸变能量不断上升. 高能量状态的位错对是不稳定的, 当达到临界值时, 它就分解成2个位错对, 并且释放出能量, 使位错处于较低的能量状态. 图1a和b中位错A分解成位错A₁和A₂, 围绕位错A, A₁和A₂选取适当的模拟区域计算得到位错A分解过程的自由能密度与时间步数关系曲线如图3a所示. 图1a~c中位错B分解成位错B₁和B₂, 围绕位错B, B₁和B₂选取适当的模拟区域计算得到位错B分解过程的自由能密度与时间关系曲线如图3b所示.

显示原图| 下载原图ZIP| 生成PPT

图3

Fig.3 位错分解过程的自由能-时间曲线

图3a和b曲线上的实心圆圈处的自由能为极大值, 在此之前晶界位错对在应力作用下作攀移运动并累积能量, 当应变达到阈值后, 位错对便发生分解. 在实心圆圈处之后的时间, 位错对发生分解, 位错的自由能下降. 对比图3a和b可见, 图1a中的位错对A的初始能量稍高些, 并且先于位错对B达到极大值, 因此, 位错对A先于位错对B而分解. 在时间步为27380时位错对A的自由能达到极大值0.15776 J而分解；位错对B直到时间步为27880时其自由能才达到极大值0.15786 J, 然后发生分解. 模拟结果显示两者的自由能极大值基本相同, 或者说不同的位错对分解时其临界能量值基本相同. 由图3a和b得到, 对应的A位错对的分解激活能为0.00096 J, 对应的B位错对的分解激活能为0.00146 J. 可见, B位错对的激活能较高, 较晚发生分解.

3.3.2 位错在晶粒内相遇湮没 2个Burgers矢量方向完全相反的位错相遇会发生湮没, 并释放出能量. 图1b和c中位错A₂和D₁在晶粒内相遇湮没, 围绕位错A₂和D₁选取适当的区域模拟计算得到位错相遇湮没过程的自由能随时间变化的曲线如图4所示. 曲线最初上升阶段是由于2个位错逐渐靠近时, 引起区域畸变程度变大, 因此自由能有一个上升的过程. 随着这2个位错相遇, 畸变很快变小以至消除, 畸变能得以释放, 自由能也很快下降至极小值(图4的实心圆圈处), 这时, 2个位错就完成了湮没.

3.3.3 位错被晶界吸收或与晶界位错合并 2个Burgers矢量方向不完全相反的位错相遇可以合并成一个新位错组, 并改变原来的运动方向, 同时释放畸变能量. 由图1可见, 晶界吸收穿过晶粒内部的滑移位错的过程就出现这种情况. 图1e和f中穿过晶粒内部的位错B₁和晶界上位错C相遇, 反应合并生成新的位错组B₁C. 围绕位错B₁, C和B₁C的位置, 选取适当的模拟区域计算得到位错合并过程的自由能密度随时间的变化曲线如图5所示. 曲线初始阶段上升也是由于两滑移位错组逐渐靠近时, 引起区域畸变程度增大, 使自由能出现一个上升的过程. 随着2个位错相遇合并, 畸变很快减小, 畸变能得到释放, 自由能也很快下降至极小值(图5的实心圆圈处), 这时就形成了新位错组B₁C.

显示原图| 下载原图ZIP| 生成PPT

图4

Fig.4 位错相遇湮没过程的自由能随时间变化曲线

显示原图| 下载原图ZIP| 生成PPT

图5

Fig.5 位错合并过程的自由能随时间变化曲线

3.4 位错反应机理

将模拟的二维三角晶格原子排列平面(见图1a~i)等效于fcc结构的(111)面的原子排列, 如图6a所示, 则(111)面上的原子排列方向如图6b所示. 图6c给出了原子排列方向与x轴的夹角θ, 图6d给出了(111)面上θ=15°时的原子密度分布图, 其中x轴相当于图6b中 $[\bar{1} 10]$ 方向. 图7a给出了对称倾侧晶界上的位错对放大图, 可以看出构成晶格位错对的2个单刃位错的多余原子面方向为 $[\bar{1} 01]$ 和 $[0 \bar{1} 1]$ , 夹角成60°, 对应的位错Burgers矢量为b₁和b₂, 与图7b的HRTEM像给出的对称倾侧晶界上的位错对结构相比较, 2者完全一致. 本工作设置的二维三角晶格原子排列方向与x轴的夹角θ=0.

显示原图| 下载原图ZIP| 生成PPT

图6

Fig.6 面心立方(fcc)晶格原子排列点阵及原子排列取向角

前文介绍了在外加应变的作用下, 对称倾侧晶界湮没的演化过程. 由图1a~i可见, 包括了如下几种位错的反应过程: 位错的分解(晶界位错发射)、位错的合并(晶界吸收位错)和位错的湮没消失. 对于位错的合并吸收过程, 图2中曲线的第4阶段, 即图1e~g所示过程, 表示晶界位错对所分解的2个位错对(B₁和B₂)运动到对面晶界而逐次被晶界吸收的过程. 在该过程中, 首先是位错B₁运动到对面晶界, 遇到对面晶界上的位错C而结合成一个复合位错B₁C, 组合成的新位错组B₁C的运动方向与原来位错的运动方向发生变化, 或者说由于位错的相互吸引作用而使晶界在吸收位错过程向着位错方向产生偏移或转动, 以减小晶界的位向差. 文献[31]也有类似报道. 图1f中的位错B₂的Burgers矢量包含有与其右边晶界处B₁C位错Burgers矢量方向相反的分量, 因此, 这2个位错是相互吸引的, 结果也使该处的晶界发生了偏移. 位错B₂继续滑移至位错组B₁C处, 两者相遇湮没消失, 完成了晶界再次吸收位错的过程, 如图1f和g所示.

对于二维三角晶格结构, 刃位错的Burgers矢量只存在6个可能的方向取向, 独立的Burgers矢量只有2个, 其他4个方向的Burgers矢量可由这2个方向的基本Burgers矢量组合而成. 因此, 发生的位错反应都可以用这2个基本Burgers矢量来表示. 同样, 对应于这6个Burgers矢量的刃位错的多余原子面方向有6个, 根据图8a中刃位错的多余原子面的原子排列方向设定, 可以给出这6个方向的矢量分别为n₁ = $[0 \bar{1} 1]$ , n₂= $[\bar{1} 01]$ , n₃= $[\bar{1} 10]$ , n₄= $[01 \bar{1}]$ , n₅= $[10 \bar{1}]$ , n₆= $[1 \bar{1} 0]$ . 以下定义b₁~b₆, B₁~B₈分别为位错b₁~b₆, B₁~B₈的Burgers矢量, 如果把二维三角晶格等效于fcc结构的(111)面的原子排列, 则对应的Burgers矢量可以写成b₁ = $(a / 2) [2 \bar{1} \bar{1}]$ , b₂= $(a / 2) [1 \bar{2} 1]$ , b₃= $(a / 2) [11 \bar{2}]$ , b₄= $(a / 2) [\bar{2} 11]$ , b₅= $(a / 2) [\bar{1} 2 \bar{1}]$ , b₆= $(a / 2) [\bar{1} \bar{1} 2]$ , 其中 $a^{} = \sqrt{2} a^{*}$ , $a$ 为fcc的晶格常数, $a^{*}$ 为二维三角晶格的原子间距. 对应的多余原子面方向与位错Burgers矢量方向满足b_i·n_i = 0. 所有6个方向的Burgers矢量b_i可用基本Burgers矢量b₁和b₂表示, 例如: b₃ =b₂-b₁, b₄ =-b₁, b₅ =-b₂, b₆ =b₁-b₂.

显示原图| 下载原图ZIP| 生成PPT

图7

Fig.7 位错对的晶体相场模拟与HRTEM像的结构图对比

显示原图| 下载原图ZIP| 生成PPT

图8

Fig.8 二维三角晶体中刃位错的多余原子面的原子排列方向和对应的刃位错的Burgers矢量的方向

假设可以忽略应力作用所引起的原子排列的晶格畸变影响, 则图9a的位错对B₁分解前所包含的2个多余半原子面的排列方向可分别近似看成为n₁= $[0 \bar{1} 1]$ 和n₂= $[\bar{1} 01]$ 方向, 对应的Burgers矢量分别为b₁和b₂ , 由图8可知, 分解后的两个位错对的Burgers矢量可分别表示为B₂=b₆+b₁和B₃=b₂+b₃. 由于b₃=-b₆, 可见, 位错对B₁分解的结果是新生成了一对符号相反的位错(b₃和b₆), 而原来的2个刃位错(b₁和b₂)继续保留, 经过重新组合, 生成两对新的位错对B₂和B₃. 该位错对分解反应方程可表示为B₁=b₂+b₁=(b₆+b₁)+(b₂+b₃)=(-b₃+b₁)+(b₂+b₃)=B₂+B₃, 即B₁=B₂+B₃, 分解后的2个位错组的Burgers矢量夹角为120°, 与原位错组的Burgers矢量方向夹角为60°. 由此可见, 位错的分解反应过程, 除了位错矢量方向变化外, 位错的滑移运动方向也发生变化.

图10的位错合并过程参照图8的位错Burgers矢量表示, 其反应可写成B₄+B₅=(b₃+b₄)+(b₂+b₁)=(b₃- b₁)+(b₂+b₁)=b₃+b₂=B₆, 即B₄+B₅=B₆, 可见, 反应的结果是一对符号相反的位错(b₁和b₄)发生湮没. 合并前的2对组合位错B₄和B₅的完整Burgers矢量之间的夹角为120°, 与合并后生成的新位错组B₆的Burgers矢量夹角为60°, 使得合并后生成的新位错组B₆滑移方向偏转了60°.

显示原图| 下载原图ZIP| 生成PPT

图9

Fig.9 1个晶界位错对分解成2个位错对的过程

显示原图| 下载原图ZIP| 生成PPT

图10

Fig.10 2个位错对合并成1个位错对的过程

由图11的位错对湮没过程, 参照图8的位错Burgers矢量表示, 其反应方程可写成B₇+B₈=(b₂+b₃)+(b₅+b₆)=(b₂+b₃)-(b₂+b₃)=0 , 即B₇+B₈=0 , 可见, 湮没反应的结果是2对符号相反的位错(b₂和b₅, b₃和b₆)发生湮没. 合并前的2个位错对B₇和B₈的Burgers矢量之间夹角为180°, 方向完全相反, 由此, 位错反应后将完全抵消.

显示原图| 下载原图ZIP| 生成PPT

图11

Fig.11 2个异号位错对发生湮没的过程

图9~11中的位错对B_i, 同样可用基本Burgers矢量b₁和b₂表示. 例如, B₁=b₂+b₁, B₂=b₆+b₁=-b₃+b₁=2b₁-b₂, B₃=b₂+b₃=2b₂-b₁, B₄=b₃+b₄=b₂, B₅=b₂+b₁, B₆=2b₂-b₁, B₇=2b₂-b₁, B₈=b₅+b₆=b₁-2b₂, 化简得B₁=(a/2)[110], B₂=(a/2)[101], B₃=(a/2)[011]. B₄=(a/2)[101], B₅=(a/2)[110], B₆=(a/2)[011], B₇=(a/2)[011], B₈=(a/2)[011].

实际上, 小角对称倾侧晶界形成的配对位错排列而成的晶界, 在外应变力的作用下, 晶界的位错对都会出现分解反应. 在某些情况下, 位错相遇湮没消失只在晶粒内部发生; 在某些情况下, 位错不会在晶粒内相遇消失, 而是穿过晶粒内部, 在对面晶界上湮没, 被晶界吸收, 即位错发生合并；而在某些情况下, 亚晶的湮没会同时出现位错在晶界内相遇湮没消失和被晶界吸收发生位错合并现象. 这些位错反应过程细节, 在实验上不易做到直接实时观测, 而在计算机模拟实验则容易做到, 这也体现出计算模拟实验的优势.

4 结论

(1) 对于二维三角原子点阵结构形成的小角度对称倾转晶界是由配对的位错对按直线规则排列构成, 位错对可以看成由2套位错Burgers矢量组成. 在稳定的小角度对称倾斜晶界中, 这些位错对间距与位向差值成反比.

(2) 取向差为6.7°的对称倾侧晶界的消失演化过程主要分为6个特征阶段: 首先是晶界位错的攀移, 然后是晶界发射位错, 即晶界位错对的分解成滑移位错, 位错作滑移运动; 接着是滑移位错穿过晶粒内部, 在对面晶界上湮没, 即被晶界吸收合并; 剩余的晶界位错继续攀移运动, 然后又出现位错分解, 晶界发射位错, 位错作攀滑移运动, 与其它滑移位错相遇湮没消失, 当所有晶界和位错全部消失, 双晶成为完整的单晶结构.

(3) 位错对沿晶界攀移时体系能量上升, 能量高的位错先分解, 然后脱离晶界滑移至晶粒内. 位错脱离晶界向晶粒内滑移的方向与晶界法向夹角约为60°, 位错的滑移速率远大于攀移速率, 约是攀移速率的30多倍.

(4) 晶界湮没过程存在3种位错反应机制: 晶界的位错分解, 位错与位错合并, 位错与位错相遇湮没. 晶界上的位错对分解的实质是产生了一对新的符号相反的Burgers矢量；位错被晶界吸收或吞没实质是滑移位错与晶界上的位错所具有的一对符号相反的Burgers矢量发生抵消; 位错对与位错对在晶粒内部相遇的湮没消失, 其实质是2个位错对之间具有的2对符号完全相反的位错Burgers矢量相互抵消.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]	Xu H J,Liu G X. Fundamentals of Materials Science. Beijing: Beijing University of Technology Press, 2001: 265 (徐恒均,刘国勋. 材料科学基础. 北京: 北京工业大学出版社, 2001: 265)
[2]	Hu G X,Cai X. Fundamentals of Materials Science. Shanghai:Shanghai Jiao Tong University Press, 2010: 99 (胡赓祥,蔡珣. 材料科学基础. 上海: 上海交通大学出版社, 2010: 99)
[3]	Bobylev S V, Ovid’ko I A.Phys Rev, 2003; 67B: 132506
[4]	Ovidko I A, Skiba N V.Scr Mater, 2012; 67: 13
[5]	Gukkin M Y, Ovidko I A.Phys Rev, 2001; 63B: 064515
[6]	Gukkin M Y, Ovidko I A.Acta Mater, 2004; 52: 3793
[7]	Hayakawa M, Yamaguchi K, Kimura M.Mater Lett, 2004; 58: 2565
[8]	Elder K R, Katakowski M, Haataja M, Grant M.Phys Rev Lett, 2002; 88: 245701
[9]	Elder K R, Grant M. Phys Rev, 2004; 70E: 51605
[10]	Stefanovic P, Haataja M, Provatas N.Phys Rev, 2009; 80E: 046107
[11]	Berry J, Grant M, Elder K R.Phys Rev, 2006; 73E: 31609
[12]	Pan S Y, Zhu M F.Acta Phys Sin, 2012; 61: 228102 (潘诗琰, 朱鸣芳. 物理学报, 2012; 61: 228102)
[13]	Chen Y, Kang X H, Li D Z.Acta Phys Sin, 2009; 58: 390 (陈云, 康秀红, 李殿中. 物理学报, 2009; 58: 390)
[14]	Gao Y J, Luo Z R, Zhang S Y, Huang C G.Acta Metall Sin, 2010; 46: 1473 (高英俊, 罗志荣, 张少义, 黄创高. 金属学报, 2010; 46: 1473)
[15]	Yang T, Chen Z, Dong W P.Acta Metall Sin, 2011; 47: 1301 (杨涛, 陈铮, 董卫平. 金属学报, 2011; 47: 1301)
[16]	Ren X, Wang J C, Yang Y J, Yang G C.Acta Phys Sin, 2010; 59: 3595 (任秀, 王锦程, 杨玉娟, 杨根仓, 物理学报, 2010; 59: 3595 )
[17]	Gao Y J, Wang J F, Luo Z R, Lu Q H, Liu Y. Chin J ComputPhys, 2013; 30: 577 (高英俊, 王江帆, 罗志荣, 卢强华, 刘瑶. 计算物理, 2013; 30: 577)
[18]	Elder K R, Huang Z, Provatas N.Phys Rev, 2010; 81E: 11602
[19]	Yu Y M, Backofen R, Voigt A.J Cryst Growth, 2011; 318: 18
[20]	Elder K R, Rossi G, Kanerva P, Sanches F, Ying S C, Granato E, Achim C V, Ala-Nissila T.Phys Rev Lett, 2012; 108: 226102
[21]	Gao Y J, Luo Z R, Huang C G, Lu Q H, Lin K.Acta Phys Sin, 2013; 62: 050507 (高英俊, 罗志荣, 黄创高, 卢强华, 林葵. 物理学报, 2013; 62: 050507)
[22]	Greenwood M, Rottler J, Provatas N. Phys Rev, 2011; 83B: 031601
[23]	Berry J, Elder K R, Grant M. Phys Rev, 2008; 77B: 224114
[24]	Gao Y J, Luo Z R, Huang L L, Lin K.Chin J Nonferrous Met, 2013; 23: 1892 (高英俊, 罗志荣, 黄礼琳, 林葵. 中国有色金属学报, 2013; 23: 1892)
[25]	Chen L Q, Shen J.Comput Phys Commun, 1998; 108: 147
[26]	Hirouchi T, Takaki T, Tomita Y.Int J Mech Sci, 2010; 52: 309
[27]	Gao Y J, Luo Z R, Hu X Y, Huang C G.Acta Metall Sin, 2010; 46: 1161 (高英俊, 罗志荣, 胡项英, 黄创高. 金属学报, 2010; 46: 1161)
[28]	Gao Y J, Luo Z R, Huang L L, Hu X Y.Acta Metall Sin, 2012; 48: 1215 (高英俊, 罗志荣, 黄礼琳, 胡项英. 金属学报, 2012; 48: 1215)
[29]	Wu K A, Voorhees P W.Acta Mater, 2012; 60: 407
[30]	Mills M J, Daw M S, Foiles S M.Ultramicroscopy, 1994; 56: 79
[31]	Shao Y F, Yao X, Zhao X, Wang S Q.Chin Phys, 2012; 21B: 083101

〈

〉

晶界位错运动与位错反应过程的晶体相场模拟*

PHASE FIELD CRYSTAL SIMULATION OF DISLOCA- TION MOVEMENT AND REACTION

1 晶体相场模型

2计算方法

2.1 数值计算与初始条件

2.2 外应力的施加

3 结果与分析

3.1 晶界的位错结构

3.2 外应力作用下的位错运动

3.3位错反应的能量变化

3.4 位错反应机理

4 结论

参考文献 文献选项 原文顺序 文献年度倒序 文中引用次数倒序 被引期刊影响因子

晶界位错运动与位错反应过程的晶体相场模拟^*

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子